Задача про мяч и биту: Попробуйте решить задачу — удается лишь 2% людей!
Попробуйте решить задачу — удается лишь 2% людей!
50% студентов Гарварда ответили неправильно. А сможете ли Вы угадать, сколько стоит мяч?
Когда речь идет об инстинктах, нам, как человеческим существам, как правило, нам на ум приходит еда и другие первостепенные потребности. Мы размышляем о возникновения жизни и смерти, или пытаемся все усложнить, хотя очень часто имеем дело с очевидными понятиями.
После того, как мы получаем «правильный» ответ, нам все равно бывает трудно его принять! Но загадки создаются именно для того, чтобы Вы взглянули на вопросы и проблемы с разных точек зрения.
Это головоломка стала головной болью даже для самых умных студентов Гарварда и для многих пользователей Интернета со всего мира. Внимательно подумайте над загадкой, так как первый ответ, который придет Вам в голову, может оказаться неверным.
«Бита и мяч стоят $ 1.10. Бита стоит на один доллар больше, чем мяч. Сколько стоит мяч?»
Большинство людей скажут, что ответ задачи – «10 центов».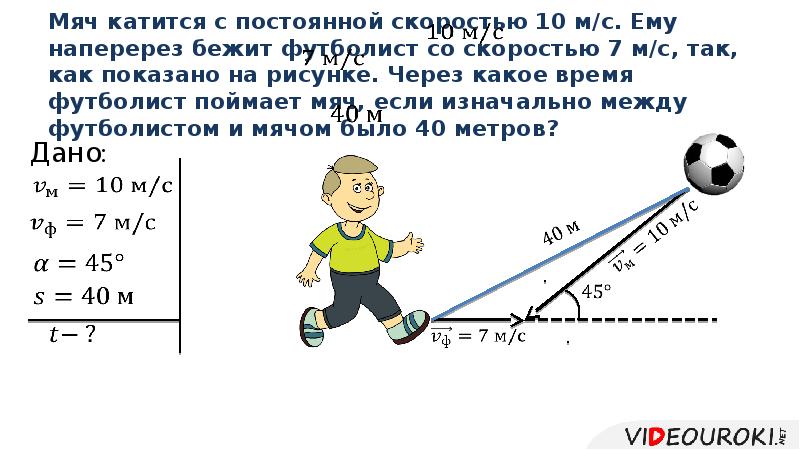 Но подумайте еще раз! Если не получилось прокрутите вниз чтоб узнать правильный ответ.
Но подумайте еще раз! Если не получилось прокрутите вниз чтоб узнать правильный ответ.
Правильный ответ «5 центов». Это происходит так: если мяч стоит 5 центов, а бита стоит $1,05 – выходит, она ровно на один доллар дороже, чем мяч – и общий итог получается $1.10.
Вот полное объяснение задачи с точки зрения Дэниела Канемана, специалиста по Поведенческой экономике, автора книги, “Думай медленно… решай быстро”:
«Число, которое пришло Вам на ум, конечно же, 10 центов . Отличительной чертой этой простой задачи является то, что она требует ответ, который является интуитивно понятным, привлекательным но неправильным. Посчитайте, и вы увидите.
Если мяч стоит 10 центов, то общая стоимость составит $ 1,20 (10 центов за мяч и $ 1.10 за биту), а не $ 1.10. Правильный ответ – 5 центов.
Можно смело предположить, что интуитивный ответ пришел на ум тем, кто в конечном итоге не смог противостоять своей интуиции.
Ответы нескольких тысяч студентов на счет этой головоломки являются шокирующими.
Более 50% студентов Гарварда, MIT и Принстона дали интуитивный, некорректный ответ …
Проблема с битой и мячом – первая из всех наблюдений, о чем говорится в этой книге: многие люди самоуверенны и склонны придавать слишком много значения своей интуиции. Они, видимо, не пытаются приложить для этого когнитивных усилий, и часто избегают сложных ответов».
На самом деле это задача несет в себе очень важный посыл: Вы оставляете свою предвзятость и действительно позволяете Вашему мозгу глубже вникнуть в суть вопроса!
Если решение по-прежнему кажется Вам запутанным, смотрите объяснение ниже!
Источник
Задачка нобелевского лауреата, или Хитрый приём маркетинга. Читайте на Cossa.ru
В 2002 году Дэниел Канеман получил Нобелевскую премию по экономике за применение психологической методики в экономической науке, в особенности — при исследовании формирования суждений и принятия решений в условиях неопределённости. Одна из задач, которую Канеман любит задавать студентам, вызывает недоумение у большинства опрошенных. Звучит она следующим образом:
Одна из задач, которую Канеман любит задавать студентам, вызывает недоумение у большинства опрошенных. Звучит она следующим образом:
Бейсбольный мяч и бита вместе стоят 1,10 доллара. Бита стоит на один доллар дороже мяча. Сколько стоит мяч?
Не спешите пролистывать эту страницу. Подумайте. Как только будете уверены в своём ответе, читайте дальше.Почти все дают интуитивный ответ: 10 центов. Так ответило большинство студентов элитных университетов Принстона и Гарварда, среди которых изначально проводили опрос. Почти все так отвечают, но это неверно.
Мяч стоит 5 центов: 1,05 доллара за биту плюс 0,05 доллара за мяч дают в сумме 1,10 доллара.
Что-то в работе мозга заставляет нас дать неверный ответ на эту простую задачу. Вместо того чтобы посчитать, мы прикидываем, что 10 центов — вполне подходящая цена для мяча, и разбиваем сумму 1,10 доллара на 1 доллар и 10 центов, соответственно. На подобных примерах Дэниел Канеман исследовал психологическую сторону процесса принятия решений. Объединив психологию с экономикой, он открыл возможности для интеграции этих двух наук и тем самым исследовал процессы принятия покупателями решений с двух сторон, двумя наборами методов.
Объединив психологию с экономикой, он открыл возможности для интеграции этих двух наук и тем самым исследовал процессы принятия покупателями решений с двух сторон, двумя наборами методов.
Только для читателей Cossa — скидка 30% на электронные книгу «Взлом маркетинга». Промокод: 1412mif.
Действует до завтра, 15 декабря, 23:59 (Мск).
P.S. Понравилось? Подписывайтесь на рассылку по бизнесу и маркетингу: раз в неделю присылаем полезные советы, ценные идеи из новинок и, конечно, особые скидки на книги — только для своих.
Как продвигать финансовые проекты в интернете?
Спецпроект о цифровых инструментах, которые помогают банкам, стартапам и другим финкомпаниям. Тексты экспертов и ничего лишнего:
- какие инструменты и подходы использовать для маркетинга;
- как распределить рекламный бюджет и настроить воронку продаж;
- какие каналы пора освоить, пока этого не сделали конкуренты;
- как развиваться и адаптировать рекламу под горячий рынок финуслуг.

Всё про диджитал для «финансов» →
Реклама
50% студентов Гарварда ответили неправильно. А сможете ли вы угадать, сколько стоит мяч?
Как реагировать на новость об измене мужа: закатить скандал или красиво поставить на место соперницу? Решать вам! Но прежде почитайте «Письмо от жены любовнице мужа», которое вызвало фурор в соцсетях!
Дорогая Людмила! Прежде всего, хочу сказать Вам, что о данном письме муж мой ничего не знает — случайно брошенная без присмотра трубка, случайно не стертые смс-ки, и все — я знаю о Вашем существовании и с интересом наблюдаю уже четвертый месяц за развитием событий в вашей трогательной Санта-Барбаре.
Причина, побудившая меня написать Вам
Это не ревность или желание защитить свою собственность. Просто сериал, который доставлял мне такое удовольствие первые пару месяцев, стал скучен и однообразен, и мне хотелось бы помочь Вам повернуть его течение в какое-нибудь более оптимистическое русло.
Во-первых хотелось бы сказать, что Вы однозначно молодец. В общем и целом тактика абсолютно правильная. Мой муж очень ленив, и сам никогда бы не вступил на кривую дорожку адьюльтера. А Ваши настойчивость и целеустремленность — это именно то, что нужно в данной ситуации.
Есть только одно маленькое НО. Не стоит его забрасывать смс-ками типа «Вы не подвезете меня сегодня до дома?», «Не пообедаем ли мы сегодня вместе?», «Не хотите ли Вы сходить в театр?». Это совершенно бесполезно. Купите уже билеты в театр и пригласите его, оплатите столик в ресторане и позовите, наврав, что у сегодня — годовщина потери невинности, в общем, берите инициативу в собственные руки — он очень занятой человек и никаких действий с его стороны Вы, все равно, не дождетесь. По крайней мере, на этом этапе.
Смс-ки типа «Я хочу Вас», «Я скучаю без Вас» тоже хороши, но когда в ответ Вы не получаете аналогичного ответа уже четвертый месяц, а только «До встречи на работе», неужели вам не хочется задуматься «Почему?» и немного сменить тактику? Итак, об ошибках. Увы и ах, но, пока Ваши шансы его совратить равны нулю.
Увы и ах, но, пока Ваши шансы его совратить равны нулю.
Вторая ошибка в том, что Вы — блондинка с прямыми волосами. Да, я внимательно изучила Вашу страничку ВКонтакте, у Вас достаточно редкое имя, чтобы без труда вычислить. Скажу сразу — Вы симпатичны. Не хочу расстраивать, но у него уже одна блондинка без сисек есть. Дома. И моя излишняя худоба, при его любви к худощавым, вообще сводят на нет Ваши преимущества передо мной. Мужчинам нужно разнообразие. Делюсь секретом. Его идеал — рыжие длинноногие барышни с пышными формами. Так что, дело за небольшим. Каблуки — не ниже 15 см, у вас же рост 162, насколько я поняла, краска для волос, ну и не самая дорогая хирургическая операция. И журавль, практически, в Ваших руках.
Третье. Это даже не ошибка, а личная моя просьба. Конспирация, конспирация и еще раз конспирация. Ну, вот, не присылай Вы ему смс-ки в час ночи, ну разве возникла бы в моей голове мысль залезть в его телефон? Да никогда. А когда муж в час ночи начинает что-то писать или, что хуже, выходить на балкон и шепотом перезванивать, то не полезть в телефон может только бревно, к которым я, рожденная в День Любопытства, ну никак не отношусь. А, всякие неожиданные открытия, заставляют нервничать мой трепетный и чувствительный организм. А нервничать я не люблю.
А когда муж в час ночи начинает что-то писать или, что хуже, выходить на балкон и шепотом перезванивать, то не полезть в телефон может только бревно, к которым я, рожденная в День Любопытства, ну никак не отношусь. А, всякие неожиданные открытия, заставляют нервничать мой трепетный и чувствительный организм. А нервничать я не люблю.
И в заключение…
Очень надеюсь, никак больше не почувствовать Ваше присутствие в его жизни, ну, кроме, может быть, его горящих глаз. В противном случае все Ваши трогательные смс-ки попадут к достопочтенному Николаю Владимировичу, указанному ВКонтакте Вашим законным супругом. Хотя, искренне верю, в Вашу благоразумность, потому как крайние меры не одобряю, да и Вы меня всем устраиваете.
Мне нравится, что Вы — замужем, мне нравится, что Вы, по отзывам моего мужа, добрая. Удачи Вам и всяческих успехов в нелегком деле совращения моего мужа. Если понадобится помощь или будут еще вопросы — я к Вашим услугам.
От жены Вашего любовника, Чебурашкиной Маши.
От редакции: Перед мудростью Женщины, написавшей это письмо своей сопернице, хочется снять шляпу и поклониться ей в пояс. Многие ли из нас умеют настолько достойно, изящно и благородно решить щекотливую ситуацию адюльтера? Вопрос оставляем открытым…
Вас также могут заинтересовать статьи:
Есть у меня подруга, 29 лет, не замужем и никогда не была в серьёзных отношенияхЧем мудрая женщина отличается от умной?
Легкий способ заполучить любого мужчину
Ленивая Система 2. Думай медленно… решай быстро
Ленивая Система 2
Одна из главных функций Системы 2 — отслеживать и контролировать мысли и действия, «предлагаемые» Системой 1, позволяя некоторым из них напрямую выражаться в поведении и подавляя или меняя другие.
Вот, к примеру, задача. Не пытайтесь ее решить, а прислушайтесь к интуиции.
Мячик и бейсбольная бита вместе стоят 1 доллар и 10 центов.
Бита стоит на доллар дороже мячика.
Сколько стоит мячик?
Вам в голову пришло число. Конечно же, вы подумали: «10 центов». Отличительная черта этой легкой задачки в том, что она вызывает в мыслях автоматический ответ — интуитивный, привлекательный, но неправильный. Посчитайте и сами увидите. Если мячик стоит 10 центов, то общая цена покупки — 1 доллар и 20 центов (10 центов за мячик и 1 доллар 10 центов за биту), а не 1 доллар 10 центов. Правильный ответ — 5 центов. Можно с уверенностью сказать, что интуитивный ответ пришел в голову и тем, кто ответил правильно, но им как-то удалось отвергнуть подсказку интуиции.
Совместно с Шейном Фредериком мы разрабатывали теорию суждений на основе двух систем, и он использовал задачу про биту и мячик для выяснения важнейшего вопроса: насколько внимательно Система 2 отслеживает предложения Системы 1? Согласно его рассуждениям, нам известен важный факт о любом, кто ответит, что мячик стоит 10 центов: этот человек не предпринял действий для проверки правильности ответа, а его Система 2 приняла интуитивную подсказку, которую могла бы опровергнуть, приложив небольшое усилие.
Задачу про мяч и биту решали тысячи студентов университетов, и результаты выглядят удручающе. Более 50 % студентов Гарварда, Принстона и Массачусетского технологического института дали интуитивный — неверный — ответ[43]. В университетах с менее строгим отбором абитуриентов не проверили себя уже более 80 %. В связи с задачей про мяч и биту мы впервые сталкиваемся с наблюдением, к которому еще не раз вернемся в этой книге: люди слишком самоуверенны, склонны чересчур доверять собственной интуиции.
Теперь я задам вам логическую задачу: две посылки и заключение. Постарайтесь как можно быстрее определить, обоснованы ли рассуждения. Следует ли заключение из посылок?
Все розы — цветы.
Некоторые цветы быстро вянут. Следовательно, некоторые розы быстро вянут.
Подавляющее большинство студентов колледжа считают этот силлогизм истинным[44]. В действительности рассуждения неверны, поскольку возможно, что среди быстро увядающих цветов нет роз. Как и с задачей про мяч и биту, в голову немедленно приходит правдоподобный ответ. Чтобы его отбросить, требуется много работы: логику непросто проверять в присутствии настойчивого убеждения «Да, все правильно!», и мало кто берет на себя труд продумать цепочку рассуждений.
Из этого эксперимента следуют обескураживающие выводы относительно повседневных решений. Выходит, что, если люди верят в истинность какого-либо утверждения, они охотно поверят даже несостоятельным аргументам в его поддержку. Но вывод Системы 1 важнее, а аргументы прилагаются.
Но вывод Системы 1 важнее, а аргументы прилагаются.
Теперь посмотрите на следующий вопрос и быстро ответьте на него прежде, чем читать дальше:
Сколько убийств каждый год совершается в штате Мичиган?
Этот вопрос, придуманный Шейном Фредериком, — опять задание для Системы 2. «Фокус» заключается в том, вспомнит ли респондент, что в Мичигане находится Детройт, город с высоким уровнем преступности. Студентам колледжа в США это известно, и они правильно опознают Детройт как самый крупный город в Мичигане. Но знание этого факта — еще не все. Мы не всегда при необходимости вспоминаем нужное. Люди, вспоминающие, что Детройт находится в Мичигане, дают более высокую оценку уровня преступности, чем остальные, но большинство респондентов Фредерика не вспомнили о городе, когда им задавали вопрос о штате. В действительности средняя оценка испытуемых, которых спрашивали о Мичигане, меньше, чем оценки другой группы, которой задавали вопрос о количестве убийств в Детройте.
В том, что люди не подумали про Детройт, могут быть виноваты и Система 1, и Система 2. Всплывет ли в памяти город при упоминании штата, частично зависит от автоматической функции памяти. У всех она разная. Некоторые прекрасно представляют штат Мичиган: его жители наверняка знают о нем больше, чем те, кто живет где-то еще; знатоки географии вспомнят больше, чем специалисты по бейсбольной статистике; более интеллектуальные индивиды, вероятно, вообще обо всем знают больше других. Интеллект выражается не только в способности рассуждать, но и в том, чтобы находить в памяти нужный материал и, при необходимости, уделять внимание. Функция памяти принадлежит Системе 1, но, с другой стороны, у всех есть возможность притормозить и активно поискать в памяти потенциально важные факты, так же как все могут приостановиться и проверить решение задачи про биту и мяч. Пределы намеренной проверки и поиска — характеристика Системы 2, которая у всех разная.
Всплывет ли в памяти город при упоминании штата, частично зависит от автоматической функции памяти. У всех она разная. Некоторые прекрасно представляют штат Мичиган: его жители наверняка знают о нем больше, чем те, кто живет где-то еще; знатоки географии вспомнят больше, чем специалисты по бейсбольной статистике; более интеллектуальные индивиды, вероятно, вообще обо всем знают больше других. Интеллект выражается не только в способности рассуждать, но и в том, чтобы находить в памяти нужный материал и, при необходимости, уделять внимание. Функция памяти принадлежит Системе 1, но, с другой стороны, у всех есть возможность притормозить и активно поискать в памяти потенциально важные факты, так же как все могут приостановиться и проверить решение задачи про биту и мяч. Пределы намеренной проверки и поиска — характеристика Системы 2, которая у всех разная.
У задачи про биту и мяч, силлогизма про цветы и вопроса про Мичиган и Детройт есть кое-что общее. Неправильные ответы на эти мини-тесты, как представляется, частично был и даны из-за слабой мотивации или из-за недостаточных усилий. Любой абитуриент, способный поступить в хороший университет, в состоянии верно решить первые две задачи и вспомнить крупнейший город штата Мичиган и его проблему с преступностью. Эти студенты способны решать сложные задачи, когда у них нет соблазна принять на веру поверхностно убедительный ответ, легко приходящий на ум. Беспокоит именно легкость, с которой они удовлетворяются решением и перестают думать. Леность самоконтроля этих молодых людей и их Системы 2 — довольно жесткое, но вряд ли несправедливое определение. Тех, кто избегает греха интеллектуальной лености, можно называть «вовлеченными». Они внимательнее, интеллектуально активнее, менее склонны удовлетворяться поверхностно привлекательными ответами, более скептически относятся к своей интуиции. Психолог Кейт Станович назвал бы их более рациональными[45].
Любой абитуриент, способный поступить в хороший университет, в состоянии верно решить первые две задачи и вспомнить крупнейший город штата Мичиган и его проблему с преступностью. Эти студенты способны решать сложные задачи, когда у них нет соблазна принять на веру поверхностно убедительный ответ, легко приходящий на ум. Беспокоит именно легкость, с которой они удовлетворяются решением и перестают думать. Леность самоконтроля этих молодых людей и их Системы 2 — довольно жесткое, но вряд ли несправедливое определение. Тех, кто избегает греха интеллектуальной лености, можно называть «вовлеченными». Они внимательнее, интеллектуально активнее, менее склонны удовлетворяться поверхностно привлекательными ответами, более скептически относятся к своей интуиции. Психолог Кейт Станович назвал бы их более рациональными[45].
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесЧто такое бейсбол и как он повлиял на английский — Skyeng Magazine
Три вещи, которыми США будут славиться даже через две тысячи лет: конституция, джаз и бейсбол. Так сказал доктор Джералд Эрли из Вашингтонского университета.
Так сказал доктор Джералд Эрли из Вашингтонского университета.
Мы не знаем, что будет через две тысячи лет. Но то, что бейсбол — великая американская игра, это факт. Четыре базы — четыре блока в нашем разборе бейсбола. Сделаете полный круг и доберетесь до конца?
В бейсболе соревнуются две команды: одна нападает, другая защищается. Цель нападающих — сделать как можно больше пробежек от базы до базы. Всего их четыре: домашняя, первая, вторая и третья. Цель защиты — помешать нападающим.
Ключевой нападающий называется batter (бэттер, бьющий). Он стоит рядом с домашней базой и держит в руках биту. Его задача — отбить мячик. Если бэттер круто отобьет мяч, у него и его товарищей по команде появится возможность перебежать на другие базы. А это то, что нужно нападающим.
За спиной бэттера-нападающего сидит catcher (кэтчер, ловец) со знаменитой огромной перчаткой. Он из команды защиты. Он ловит мяч, если его не отбил бэттер, и защищает дом.
Мячик бэттеру кидает pitcher (питчер, подающий мяч). Он игрок команды защиты. Его задача — обхитрить бэттера и кинуть мячик так, чтобы противник его не поймал или поймал не правильно.
Если бэттер плохо работает и не ловит мячи, его отправляют в аут и заменяют другим игроком из команды нападающих. Когда защитники отправляют трех нападающих в аут, команды меняются местами. За один матч команды меняются местами 9 раз.
Словарик бейсболиста
Base — база
Bat — бита
Mitt — бейсбольная перчатка
Hit and run — ударь и беги, момент, когда бэттер отбивает мяч и бежит к базе
Diamond — бриллиант, или все 4 базы (по форме поля)
Batter — бэттер, бьющий по мячу битой
Pitcher — питчер, подающий мяч
Catcher — кэтчер, ловец
Inning — подача, иннинг. Таймы в бейсболе, обычно их 9
1. Бейсбол объединяет семьи. Маленькие американцы играют с папами в мячик: один из них надевает перчатку, другой кидает мяч. Без биты и базы, но очень похоже на бейсбол. Это называется play catch with dad.
Бейсбол объединяет семьи. Маленькие американцы играют с папами в мячик: один из них надевает перчатку, другой кидает мяч. Без биты и базы, но очень похоже на бейсбол. Это называется play catch with dad.
2. Бейсбол дает почувствовать причастность к своему родному городу. В Бостоне болеют за Boston Red Sox, в Техасе — за Texas Rangers, в Чикаго — за Chicago Cubs.
Ким
преподаватель Skyeng
Я родилась и выросла в Детройте. Когда мы шли смотреть бейсбол всей семьей, я надевала футболку с тигром и точно знала, что мои ребята — Detroit Tigers. Мне было 6 лет.
3. Бейсбол — это праздник, у которого есть свои традиции. Еда бейсбола — хот-дог. На матче все вместе поют «Take Me Out To The Ball Game» — гимн игры, который знает каждый американец. В перерыве зрители встают, чтобы размяться и выпить баночку пива — это называется seventh-inning stretch (растяжка после седьмого иннинга).
Приемы из бейсбола стали идиомами и перекочевали в разговорную речь.
Hit a home run — «преуспеть в чем-то, затащить». Когда бэттер отбивает мяч, успевает обежать все базы и вернуться на домашнюю базу — это большой успех.
I think I really hit a home run on my job interview yesterday.
Я думаю, что я и правда затащил вчерашнее интервью на работу.
Throw a curve ball — «удивить кого-то чем-то неожиданным». Когда питчер бросает мяч, он может его закрутить. Для бэттера это сюрприз, и он не сможет поймать мячик.
She really threw me a curve ball when she told me last minute that she couldn’t marry me.
Она меня удивила, когда сказала в последний момент, что не может выйти за меня замуж.
Touch base — «быстро с кем-то переговорить». Когда игроки обегают базы, им нужно слегка до них докоснуться.
I ran into him at the street, and we touched a base.
Я вчера столкнулся с ним на улице, и мы переговорили.
Right off the bat — «с места в карьер, сразу же». Так происходит, когда бэттер сразу же отбивает мяч битой.
I could tell they liked each other right off the bat.
Я понял, что они сразу же понравились друг другу.
Ну и конечно, благодаря бейсболу появились выражения вроде «дойти до второй базы». Вот как они расшифровываются:
First base = kissing
Second base = all kind of touches with clothes
Third base = all kind of touches without clothes
Home base = sex
Первая база = поцелуи
Вторая база = все виды касаний через одежду
Третья база = все виды касаний без одежды
Четвертая база = секс
Американцы сняли много классных фильмов о бейсболе. Посмотрите их в оригинале, чтобы проникнуться атмосферой и прокачать английский. Наш топ-3:
- Field of dreams («Поле мечты») — история о фермере, которые превращает свое кукурузное поле в поле для бейсбола, и на нем играют величайшие бейсболисты-призраки (и фермер не сошел с ума!).

- The Bad News Bears («Несносные медведи») — сына очень активной мамы не берут в бейсбол, и она решает сделать команду из мальчишек-лузеров под руководством питчера-алкоголика (получается круто и смешно).
- Moneyball («Человек, который изменил все») — драма о команде «Окленд Атлетикс» и их менеджере, который ненавидит проигрывать, с Брэдом Питтом в главной роли (получается вдохновляюще).
Поздравляем, вы вернулись на домашнюю базу! Ловите бесплатные материалы по английскому — раз в неделю.
Еженедельные учебные материалы по английскому
Словарь, грамматика и видео на определенную тему + анонсы и подарки от друзей.
Скоро на имейл вам придет письмо с инструкцией. А пока запишитесь на бесплатное онлайн-занятие с преподавателем и получите в подарок еще 2 урока.
Получить 2 урока
Обрабатываем заявку
Скоро на имейл вам придет письмо с инструкцией. А в течение часа мы позвоним и подберем удобное время занятия. Продуктивного дня 🙂
А в течение часа мы позвоним и подберем удобное время занятия. Продуктивного дня 🙂
Ой, произошла ошибка обработки. Попробуйте еще раз чуть позднее.
Ой, произошла ошибка обработки. Скорее всего, такой имейл или телефон уже зарегистрирован.
Задачки для Системы 1 и 2 из книги Д.Канемана «Думай медленно… Решай быстро»
Читаю книгу Даниэля Канемана «Думай медленно… Решай быстро» про то, как устроен наш мозг, и почему случаются когнитивные искажения.Долго уже читаю… Книга безумно интересная, но такая длинная, что постоянно хочется ее забросить 😃. Но я не сдаюсь.
Осилила только четверть книги (из 716 страниц), но уже хочу с вами поделиться приобретенными знаниями.
Знать бы только, куда эти знания потратить. Как пишет сам автор, не допускать когнитивных искажений, даже зная все написанное, очень сложно — Система 2 нашего мозга (название автора), которая думает медленно и основательно, очень ленива в отличие от быстрой и доверчивой Системы 1.
 Автор все же предлагает и описывает способы, как можно не допустить ошибок мышления.
Автор все же предлагает и описывает способы, как можно не допустить ошибок мышления.Когнитивные искажения — систематические отклонения в поведении, восприятии и мышлении, обусловленные субъективными предубеждениями и стереотипами, социальными, моральными и эмоциональными причинами, сбоями в обработке и анализе информации, а также физическими ограничениями и особенностями строения человеческого мозга (Википедия).
«Вот, к примеру, задача. Не пытайтесь ее решить, а прислушайтесь к интуиции.
Мячик и бейсбольная бита вместе стоят 1 доллар и 10 центов.
Бита стоит на доллар дороже мячика.
Сколько стоит мячик?
Вам в голову пришло число. Конечно же, вы подумали: «10 центов». Отличительная черта этой легкой задачки в том, что она вызывает в мыслях автоматический ответ – интуитивный, привлекательный, но неправильный. Посчитайте и сами увидите.»
«Если 5 машин за 5 минут делают 5 деталей, то за какое время 100 машин сделают 100 деталей?
100 минут ИЛИ 5 минут?»
«Главное – любым способом уменьшить когнитивное напряжение, так что для начала следует сделать все возможное для повышения читабельности.
 Сравните два утверждения.
Сравните два утверждения.Адольф Гитлер родился в 1892 году.
Адольф Гитлер родился в 1887 году.
Оба эти утверждения неверны (Гитлер родился в 1889-м), но эксперименты показали, что первому поверят скорее.»
» Откуда вы знаете, что утверждение верно? Если оно логически или ассоциативно увязывается с другими вашими убеждениями и предпочтениями или исходит из источника, которому вы доверяете и симпатизируете, вы почувствуете когнитивную легкость. Проблема состоит в том, что у легкости могут быть и другие причины, в том числе вид шрифта и привлекательный ритм прозы, а у вас нет простого способа отследить источник своих чувств. «
» «Сколько животных каждого вида взял в ковчег Моисей?«
Мало кто замечает подвох в этом вопросе, носящем название «иллюзия Моисея». Животных в ковчег набирал не Моисей, а Ной. Как и случай с гримасничающим посетителем ресторана, эта иллюзия хорошо объясняется теорией нормы. Мысль о набранных в ковчег животных формирует библейский контекст, и Моисей в нем вполне нормален.
«При вопросе «Дружелюбен ли Сэм?» вам в голову придет много примеров поведения Сэма – совсем иных, чем при вопросе «Враждебен ли Сэм?». Система 2 проверяет гипотезы, используя целенаправленный поиск доказательств, называемый стратегией позитивного тестирования. Вопреки наставлениям теоретиков, рекомендующих проверять гипотезы путем их опровержения, многие (а зачастую и сами исследователи) ищут данные, которые, вероятнее всего, будут соответствовать их текущим убеждениям. Склонность Системы 1 к подтверждению благоприятствует некритическому принятию предложений и преувеличению вероятности экстремальных и маловероятных событий.
 «
««Если вам нравится политика президента, вам, вероятно, также нравятся его внешность и голос. Склонность хорошо (или плохо) воспринимать в человеке все, включая то, чего вы не видели, называется эффектом ореола.»
«Эффект фрейминга: разные способы подачи одной и той же информации часто вызывают разные эмоции. Утверждение «Выживаемость в течение месяца после операции составляет 90 %» успокаивает больше, чем эквивалентное утверждение «Смертность в течение месяца после операции составляет 10 %». Аналогично продукты с описанием «на 90 % без жира» более привлекательны, чем те, на которых написано: «содержание жира 10 %». Эквивалентность формулировок очевидна, но человек обычно видит лишь одну из них, а для него существует только то, что он видит.»
» Возьмите лист бумаги и проведите от нижнего края вверх линию длиной в 6 см – без линейки. Теперь возьмите другой лист и начертите на нем – от верхнего края вниз – линию, на 6 см не доходящую до противоположного края.
 Сравните нарисованное. Весьма вероятно, что ваша первая оценка шести сантиметров окажется короче второй. Это потому, что вы точно не знаете, как выглядит такая линия, – существует некоторая неопределенность. Начиная снизу, вы останавливаетесь у нижней границы области неопределенности, а начиная сверху – у верхней.»
Сравните нарисованное. Весьма вероятно, что ваша первая оценка шести сантиметров окажется короче второй. Это потому, что вы точно не знаете, как выглядит такая линия, – существует некоторая неопределенность. Начиная снизу, вы останавливаетесь у нижней границы области неопределенности, а начиная сверху – у верхней.»Это далеко не все, что я отметила в цитаты, пока читала. Пока я делюсь только ими. Очень сложно уместить все знания в один пост. Так и автор не смог 😃
В следующих постах я выпишу список когнитивных искажений, их причин и ошибок от когнитивной легкости, про которые узнаю в книге. Думаю, это будет после ее полного прочтения.
Задача, на которой «ломаются» студенты Гарварда
Большая часть студентов одного их самых престижных университетов мира попадает в ловушку, созданную их же интуицией, и устно отвечает неправильно на вопрос, который школьники расписывают в простейшее уравнение на четвертом году обучения. Об этом сообщает в своей книге «Думать медленно и быстро» (Thinking, Fast And Slow) лауреат Нобелевской премии по экономике, профессор психологии Даниэль Канеман.
Об этом сообщает в своей книге «Думать медленно и быстро» (Thinking, Fast And Slow) лауреат Нобелевской премии по экономике, профессор психологии Даниэль Канеман.
Задача может формулироваться по-разному, но суть одна:
Тут бы студентам и смекнуть, что их хотят запутать простым вопросом, но большинство, не задумываясь, отвечает — 10 центов. Однако это неправильный ответ.
Сейчас мы объясним почему.
Отличительная особенность этой простой задачки в том, что она провоцирует на интуитивный ответ, который равен 10 центам и является неверным. Если вы прибегните к математике, то поймете почему.
Так, если мяч стоит 10 центов, то тогда общая сумма получится 1,2 доллара (10 центов за мяч и 1,1 доллара за биту), а не 1,1 доллара.
Давайте назначим стоимость мяча в качестве переменной х, а биты как х + 1.
Это означает, что х + (х + 1) = $ 1,10
Решаем простейшее уравнение и получаем правильный ответ: 5 центов.
Много тысяч студентов отвечали на этот вопрос про мяч и биту, и результаты оказались шокирующими, сообщает Канеман. Более половины студентов Гарварда, Массачусетского технологического института и Принстонского университета дали неправильный интуитивный ответ. В менее отборных университетах цифра оказалась и того больше – свыше 80% неверных ответов.
Данный вопрос «мяча и биты» является первым, который рассматривается в книге Нобелевского лауреата: многие люди чрезмерно уверены в себе и слишком сильно полагаются на свою интуицию. Похоже, что они рассматривают попытку подумать, как не очень приятную идею, и по возможности избегают ее.
А вы дали правильный ответ?
Задача на логику: откуда взялся лишний рубль?
Задача на логику, которую решали в разведшколах
Новый поворот в классической головоломке — Ассоциация психологической науки — APS
«Бита и мяч в сумме стоят 1,10 доллара. Бита стоит на 1 доллар дороже мяча. Сколько стоит мяч? »
Бита стоит на 1 доллар дороже мяча. Сколько стоит мяч? »
Подумайте на минутку … У вас есть ответ? Многие в ответ говорят, что мяч должен стоить 10 центов. Это тот ответ, который вы придумали? Хотя этот ответ интуитивно приходит в голову, он неверен. Если мяч стоит 10 центов, а бита — 1 доллар.00 больше, чем мяч, то бита будет стоить 1,10 доллара на общую сумму 1,20 доллара. Правильный ответ на эту проблему: мяч стоит 5 центов, а бита — на доллар дороже — 1,05 доллара, что в сумме составляет 1,10 доллара.
Так почему же так много людей отвечают неправильно? Ответ заключается в том, что люди часто заменяют сложные проблемы более простыми, чтобы быстро их решить. В этом случае люди, кажется, неосознанно подставляют в задачу выражение «больше чем» (летучая мышь стоит 1 доллар.00 больше, чем мяч) с абсолютным утверждением (бита стоит 1 доллар США). Это упрощает работу с математикой; если мяч и бита вместе стоят 1,10 доллара, а бита — 1 доллар, то мяч должен стоить 10 центов.
Снова и снова исследования с использованием проблемы биты и мяча показали, что этот интуитивный процесс сбивает людей с пути. Но всегда ли интуиция мешает решению проблем? В статье журнала Journal of Cognitive Psychology за 2014 год исследователь Университета Тулузы Бастьен Тремольер и исследователь Университета Париж-Декарт Вим Де Нейс попытались ответить на этот вопрос.
Тремольер и Де Нейс отмечают, что интуитивно сгенерированный ответ на проблему с битой и мячом (что мяч стоит 10 центов) нельзя назвать ни в высшей степени правдоподобным, ни в высшей степени невероятным. Есть основания полагать — особенно для тех, кто не является экспертом в бейсболе, — что такой мяч может стоить 10 центов. Они задавались вопросом, как человек мог бы отреагировать, если бы подобная проблема вызвала интуитивный, но невероятный ответ. Что бы произошло, если бы интуитивный ответ противоречил другим интуитивным представлениям, таким как прошлые знания о стоимости предмета?
Чтобы выяснить это, исследователи попросили участников ответить на классическую или модифицированную задачу типа «бита и мяч». В классической задаче участникам был задан следующий вопрос:
В классической задаче участникам был задан следующий вопрос:
«Роллс-Ройс и Феррари вместе стоят 190 000 долларов. Rolls-Royce стоит на 100 000 долларов больше, чем Ferrari. Сколько стоит Феррари? »
В модифицированной версии задачи участникам был задан следующий вопрос:
«Феррари и Форд вместе стоят 190 000 долларов. Ferrari стоит на 100 000 долларов больше, чем Ford. Сколько стоит Форд? »
Как и в исходной задаче с битой и мячом, люди часто пытаются сделать задачу проще, неосознанно удаляя из нее формулировку «больше чем», что заставляет их читать проблему так: «Роллс-Ройс стоит 100 000 долларов. »Или« Феррари стоит 100 000 долларов.”
Интуитивно понятный, но неверный ответ состоит в том, что менее дорогой автомобиль (Феррари или Форд, в зависимости от проблемы) стоит 90 000 долларов; однако в модифицированной версии задачи этот ответ (что Ford стоит 90 000 долларов) противоречит предыдущим знаниям людей об автомобилях Ford: идея о том, что Ford такой дорогой, не является правдоподобным. Этого конфликта нет в классической задаче, поскольку мысль о Ferrari стоимостью 90 000 долларов показалась бы большинству людей разумной.
Этого конфликта нет в классической задаче, поскольку мысль о Ferrari стоимостью 90 000 долларов показалась бы большинству людей разумной.
Исследователи обнаружили, что значительно больше людей правильно ответили на модифицированную версию задачи, чем на классическую.Авторы утверждали, что когда интуитивные ответы вступают в противоречие с другими интуициями, например, основанными на прошлых знаниях, люди с большей вероятностью будут участвовать в более осознанных и рефлексивных рассуждениях, что приводит к более высокой вероятности того, что они ответят на проблему правильно.
АртикулТремольер, Б., и Де Нейс, В. (2014). Когда интуиция полезна: предыдущие убеждения могут поддержать рассуждение в проблеме биты и мяча. Журнал когнитивной психологии , 26 , 486–490.
Алгебраические рассуждения и варианты задач с битой и мячом: сначала решение изоморфной алгебры облегчает решение задач позже
участников
Сотня участников была набрана онлайн через Amazon Mechanical Turk ( M Возраст = 26,04, SD = 6,31, диапазон = 18-49, мужчины = 69%) и 97 студентов-психологов из Университета Колорадо ( M Возраст = 19. 38, SD = 1.09, диапазон = 18-22, мужчины = 51%) были набраны в качестве лабораторных участников. Онлайн-участники были ограничены текущими студентами колледжа (указанными через самоотчет) не моложе 18 лет, чтобы быть сопоставимыми с лабораторной выборкой.
38, SD = 1.09, диапазон = 18-22, мужчины = 51%) были набраны в качестве лабораторных участников. Онлайн-участники были ограничены текущими студентами колледжа (указанными через самоотчет) не моложе 18 лет, чтобы быть сопоставимыми с лабораторной выборкой.
Материалы и процедура
Опросы были разработаны в программном обеспечении Qualtrics для проведения опросов и распространены через Amazon Mechanical Turk для онлайн-выборки. Онлайн-участников попросили предоставить свои собственные бумаги и письменные принадлежности для решения математических задач.Участники лаборатории были протестированы в рамках того же набора опросов на настольных компьютерах iMac. Карандаши и бумага были предоставлены участникам лаборатории, у которых не было этих предметов.
Предметы и их количества, использованные в условиях репликации, следуют De Neys et al. (2013): Вместо летучей мыши / мяча / 1,10 доллара уравновешенными вариантами задач были карандаш / ластик / 1,10 доллара и журнал / банан / 2,90 доллара (2,90 доллара вместо 1,10 доллара и 2,00 доллара вместо 1 доллара). Ожидается, что в вопросе журнал / банан / 2,90 доллара предвзятые участники склонны вычесть 2 доллара.00 от 2,90 долларов с такой же интуитивной простотой, как 1 доллар от 1,10 доллара. Более того, проблема с битой и мячом стала довольно известной, поэтому включение этих альтернативных вопросов должно было ограничить любое возможное улучшение производительности из-за предыдущего воздействия. Кроме того, после каждого критического вопроса участники получали рейтинг доверия со следующей подсказкой: «Насколько вы уверены в своем ответе? Запишите число от 0% (совершенно не уверен) до 100% (полностью уверен) ».
Ожидается, что в вопросе журнал / банан / 2,90 доллара предвзятые участники склонны вычесть 2 доллара.00 от 2,90 долларов с такой же интуитивной простотой, как 1 доллар от 1,10 доллара. Более того, проблема с битой и мячом стала довольно известной, поэтому включение этих альтернативных вопросов должно было ограничить любое возможное улучшение производительности из-за предыдущего воздействия. Кроме того, после каждого критического вопроса участники получали рейтинг доверия со следующей подсказкой: «Насколько вы уверены в своем ответе? Запишите число от 0% (совершенно не уверен) до 100% (полностью уверен) ».
Описание условий поиска
Обзор
Ни по одному из вопросов не было получено отзывов.Все участники в каждом сигнальном условии решили один вариант проблемы в его стандартной форме как критический вопрос, уравновешенный таким образом, что половине участников из каждого источника был предоставлен один вариант, а другой половине — другой вариант. В одном из условий (контроль без начальной проблемы) участникам показали только критический вопрос за карандаш / ластик / 1,10 доллара или критический вопрос из журнала / банана / 2,90 доллара, оба в их стандартной форме. Во всех других условиях реплики критическому вопросу предшествовала реплика.В одном из этих условий реплики (не относящейся к алгебре) реплика была несвязанной проблемой алгебры. В остальных условиях реплика реплика была некой формой альтернативной задачи. Таким образом, участники никогда не видели ни одного варианта задачи, ни уравнения, соответствующего варианту задачи, более одного раза.
В одном из условий (контроль без начальной проблемы) участникам показали только критический вопрос за карандаш / ластик / 1,10 доллара или критический вопрос из журнала / банана / 2,90 доллара, оба в их стандартной форме. Во всех других условиях реплики критическому вопросу предшествовала реплика.В одном из этих условий реплики (не относящейся к алгебре) реплика была несвязанной проблемой алгебры. В остальных условиях реплика реплика была некой формой альтернативной задачи. Таким образом, участники никогда не видели ни одного варианта задачи, ни уравнения, соответствующего варианту задачи, более одного раза.
Алгебра плюс слова
Половине участников в этом условном сигнале первоначально был предложен следующий вопрос и соответствующие алгебраические уравнения:
Карандаш и ластик вместе стоят 1 доллар.10. Карандаш стоит на 1 доллар больше, чем ластик. Сколько стоит ластик?
$$ \ begin {array} {l} \ mathrm {P} + \ mathrm {E} = \ $ 1. 10 \ hfill \\ {} \ mathrm {P} = \ $ 1.00+ \ mathrm {E} \ hfill \\ {} \ mathrm {Solve} \ \ mathrm {for} \ \ mathrm {E} \ hfill \ end {array} $$
10 \ hfill \\ {} \ mathrm {P} = \ $ 1.00+ \ mathrm {E} \ hfill \\ {} \ mathrm {Solve} \ \ mathrm {for} \ \ mathrm {E} \ hfill \ end {array} $$
Поскольку это были дополнительные формы одного и того же вопроса, на экране опроса Qualtrics было доступно только одно текстовое поле для ответа. После этого вопроса участникам было предложено решить критический вопрос журнал / банан / 2 доллара.90 в стандартной форме (т.е. без кия):
Журнал и банан вместе стоят 2,90 доллара. Журнал стоит на 2 доллара дороже банана. Сколько стоит банан?
Оставшаяся половина участников в этом условии была уравновешена таким образом, что их исходной репликой была задача журнала / банана / 2,90 доллара и соответствующие уравнения с карандашом / ластиком / 1 долларом.10 проблема в стандартной форме как критический вопрос. Цель состояла в том, чтобы ограничить двусмысленность того, что задавал вопрос, без четкого определения решения.
Только алгебра
Половина участников в этом условном сигнале была первоначально запрошена с помощью только карандаша / ластика / алгебраических уравнений стоимостью 1,10 доллара США, представленных следующим образом:
Рассмотрим следующие уравнения. Используйте метод подстановки, чтобы найти значение E
$$ \ begin {array} {l} \ mathrm {P} + \ mathrm {E} = \ $ 1.10 \ hfill \\ {} \ mathrm {P} = \ $ 1.00+ \ mathrm {E} \ hfill \\ {} \ mathrm {Solve} \ \ mathrm {for} \ \ mathrm {E} \ hfill \ end {array } $$
После этого вопроса участникам было предложено решить критический вопрос журнал / банан / $ 2,90 в его стандартной форме (то есть без соответствующих алгебраических уравнений). Чтобы уравновесить варианты задачи, оставшаяся половина участников этого условия подсказки была запрошена с помощью алгебраических уравнений журнал / банан / 2,90 доллара, и их критическим вопросом был карандаш / ластик / 1 доллар. 10 в стандартной форме. Это условие подсказки позволило нам исследовать эффект алгебраической подсказки без письменного выражения вопроса, включенного в реплику.
10 в стандартной форме. Это условие подсказки позволило нам исследовать эффект алгебраической подсказки без письменного выражения вопроса, включенного в реплику.
Алгебра неуместна
Первоначально всем участникам в этом условном сигнале был предложен следующий вопрос по алгебре:
Рассмотрим следующие уравнения. Используйте метод подстановки, чтобы найти значение X
$$ \ begin {array} {l} \ mathrm {X} +3 \ mathrm {Y} = 13 \ hfill \\ {} \ mathrm {Y} = 6 \ hbox {-} 2 \ mathrm {X} \ hfill \\ {} \ mathrm {Решить} \ \ mathrm {for} \ \ mathrm {X} \ hfill \ end {array} $$
После этого вопроса половине участников было предложено решить критический вопрос журнал / банан / 2 доллара.90 в его стандартной форме (т.е. без алгебраических уравнений). Другой половине участников было предложено решить критический вопрос карандаш / ластик / 1,10 доллара в стандартной форме. Это условие подсказки позволило нам определить эффект алгебраической подсказки в контексте проблемы алгебры, не связанной с конкретной структурой типов задач с битой и мячом.
Это условие подсказки позволило нам определить эффект алгебраической подсказки в контексте проблемы алгебры, не связанной с конкретной структурой типов задач с битой и мячом.
Управление с начальной проблемой
Половине участников в этом состоянии подсказки сначала попросили карандаш / ластик / 1 доллар.10 вопросов, за которыми следует критический вопрос журнала / банана / $ 2,90, оба в стандартной форме. Для остальных участников был изменен порядок представления вопросов. Этот контроль позволил нам определить уникальный эффект алгебраической подсказки помимо эффекта простого задания начального релевантного вопроса.
Управление без начальных проблем
Половине участников в этом условном сигнале было предложено карандаш / ластик / 1 доллар.10 критических вопросов, в то время как другой половине задавали критический вопрос журнал / банан / $ 2,90, оба в их стандартной форме без предварительной подсказки. Ожидалось, что участники продемонстрируют уровень ошибок, согласующийся с предыдущими исследованиями.
Ожидалось, что участники продемонстрируют уровень ошибок, согласующийся с предыдущими исследованиями.
Участников затем попросили заполнить анкету из пяти вопросов по математической тревоге / уверенности (MANX), чтобы определить, в какой степени общая математическая тревожность и математическая уверенность связаны с точностью решения задачи (см. Chipman, Krantz, & Silver, 1992).Участники выбрали рейтинг по пятиуровневой шкале от «полностью согласен» до «категорически не согласен» (например, «Работа над математическими задачами меня напрягает»). Низкие баллы указывают на беспокойство по поводу математики; высокие баллы свидетельствовали об уверенности в математике.
Наконец, участников попросили оценить следующий вопрос: «Насколько вы обеспокоены математикой по шкале от 1 до 10?» Эшкрафт (2002) обнаружил, что для быстрого определения математической тревожности достаточно просто задать этот вопрос, и это коррелирует с результатами по сокращенной шкале оценки математической тревожности.
Влияние повторной презентации на проблему с битой и мячом
Делаем ли мы снижение предвзятости ?: Влияние повторной презентации на проблему с битой и мячомСуждение и принятие решений, Том. 14, No. 2, март 2019, стр. 170-178.
Матье Раоэлисон* Вим Де Нейс # |
Печально известная проблема с битой и мячом уже давно используется для демонстрации
что люди легко поддаются влиянию своей интуиции.В этой статье мы
проверить надежность предвзятого ответа, изучив, как
затронуты повторным представлением проблемы. Участники решили 50
стандартная и контрольная версии задачи о мячике и бите. Изучить
характер потенциального обучающего эффекта мы приняли двухрежимный
парадигма, в которой участники должны дать первую догадку и могут
потом найдите время, чтобы обдумать и изменить свой ответ. Полученные результаты
показали, что как первые догадки людей, так и их ответы
после обдумывания преимущественно оставался предвзятым от начала до конца. Но в тех редких случаях, когда участники научились исправлять
сами они сразу сумели применить стратегию решения и
дал правильное представление о последующих проблемах. Обсуждаем критические
методологические и теоретические выводы.
Но в тех редких случаях, когда участники научились исправлять
сами они сразу сумели применить стратегию решения и
дал правильное представление о последующих проблемах. Обсуждаем критические
методологические и теоретические выводы.
Ключевые слова: бита и мяч, предвзятость, рассуждение, принятие решений, обучение.
1 Введение
Десятилетия исследований суждений и принятия решений показали, что человеческое мышление часто оказывается предвзятым из-за ошибочной интуиции.В распространенность этого предубеждения иногда приводила к характеристике люди, рассуждающие как люди, скупые на познание, склонные чрезмерно полагаться на легкие интуитивное мышление (Канеман, 2011). Пожалуй, один из самых знаменитым примером этого явления является проблема биты и мяча. (Фредерик, 2005):
Бита и мяч в сумме стоят 1,10 доллара. Летучая мышь стоит на 1 доллар больше, чем шар. Сколько стоит мяч?
Интуитивно приходит на ум ответ 10 центов. Это
также ответ, что большинство участников
сталкиваются с проблемой биты и мяча, как правило, уступают. Однако после
после некоторого дальнейшего размышления станет ясно, что этот ответ неверен:
если мяч стоит 10 центов, то бита — на доллар дороже — будет
стоимость 1,10 доллара, в результате чего в общей сложности 1,20 доллара. Кажется, проблема в
что люди вполне естественно разбирают 1,10 доллара в 1 доллар и 10 центов, и
просто не обращайте внимания на критическое утверждение «больше чем» (Канеман, 2011).
Однако после
после некоторого дальнейшего размышления станет ясно, что этот ответ неверен:
если мяч стоит 10 центов, то бита — на доллар дороже — будет
стоимость 1,10 доллара, в результате чего в общей сложности 1,20 доллара. Кажется, проблема в
что люди вполне естественно разбирают 1,10 доллара в 1 доллар и 10 центов, и
просто не обращайте внимания на критическое утверждение «больше чем» (Канеман, 2011).
Теоретически решить проблему с битой и мячом не должно быть слишком сложно. Это сводится к решению основного алгебраического уравнения «X + Y = 1.10, Y = 1 + X, реши для X »- то, что уже давно сделали самые образованные взрослые. в своих классах математики в старшей школе (Hoover & Healy, 2017). Тем не менее, интуитивная привлекательность ответа «10 центов» кажется имеют непреодолимое влияние на мышление людей и сбивают их с пути (Баго, Раоэлисон и Де Нейс, 2019; Фредерик, 2005).
В этой статье мы стремимся проверить распространенность предвзятого ответа в
проблема с битой и мячом. Наш основной интерес состоит в том, чтобы проверить, проявляют ли разумные
любые свидетельства спонтанного обучения при многократном решении таких проблем, как
проблема биты и мяча.Самые классические задачи по эвристике и предвзятости
поле — в том числе битой и мячом — являются «одноразовыми» проблемами (Канеман,
2002, 2011): участникам обычно дарят одну единственную
пробный. Неявное предположение состоит в том, что повторное представление проблемы может
вызвать эффект подсказки или обучения и тем самым искусственно повысить
представление. Однако прямого тестирования этого
предположение. Теоретически потенциальный эффект спонтанного обучения будет
интересно. Если просто повторное представление проблемы (т.е., не будучи
явным образом проинструктирован или получен обратная связь) помогает людям избежать предвзятого
(неверный) ответ, это рисует менее мрачную картину человеческого
возможности. В первый раз мы можем быть когнитивными скупцами, но если мы
сумели спонтанно исправить себя, это может означать, что наша предвзятость
а скупость менее глубока, чем часто думают.
Наш основной интерес состоит в том, чтобы проверить, проявляют ли разумные
любые свидетельства спонтанного обучения при многократном решении таких проблем, как
проблема биты и мяча.Самые классические задачи по эвристике и предвзятости
поле — в том числе битой и мячом — являются «одноразовыми» проблемами (Канеман,
2002, 2011): участникам обычно дарят одну единственную
пробный. Неявное предположение состоит в том, что повторное представление проблемы может
вызвать эффект подсказки или обучения и тем самым искусственно повысить
представление. Однако прямого тестирования этого
предположение. Теоретически потенциальный эффект спонтанного обучения будет
интересно. Если просто повторное представление проблемы (т.е., не будучи
явным образом проинструктирован или получен обратная связь) помогает людям избежать предвзятого
(неверный) ответ, это рисует менее мрачную картину человеческого
возможности. В первый раз мы можем быть когнитивными скупцами, но если мы
сумели спонтанно исправить себя, это может означать, что наша предвзятость
а скупость менее глубока, чем часто думают. Очевидно, из более
с образовательной точки зрения, это также укажет путь к дешевому и
прямое вмешательство по устранению предвзятости.Тестирование эффекта повторного
презентация важна и с методологической точки зрения.
Различные методы визуализации (например, ЭЭГ, фМРТ) и поведенческие методы (например, задержка
анализов) обычно требуют представления нескольких испытаний, чтобы получить
надежное соотношение сигнал / шум. В этом отношении важно знать, как
стабильная работа людей проходит испытания.
Очевидно, из более
с образовательной точки зрения, это также укажет путь к дешевому и
прямое вмешательство по устранению предвзятости.Тестирование эффекта повторного
презентация важна и с методологической точки зрения.
Различные методы визуализации (например, ЭЭГ, фМРТ) и поведенческие методы (например, задержка
анализов) обычно требуют представления нескольких испытаний, чтобы получить
надежное соотношение сигнал / шум. В этом отношении важно знать, как
стабильная работа людей проходит испытания.
Интересно, что некоторые предшествующие косвенные данные свидетельствуют о том, что повторяющиеся
Воздействие может вызвать обучающий эффект в решении проблемы с битой и мячом.Бита и мяч — одна из проблем, присущих когнитивной
Тест на отражение (CRT, Frederick, 2005) — короткий тест, который часто
используется для измерения склонности людей размышлять об их интуитивном
суждения. Этот тест часто включается в качестве предиктора в (онлайн)
исследования (Stewart, Chandler, & Paolacci, 2017; Stagnaro, Pennycook & Rand,
2018; Томсон и Оппенгеймер, 2016). Было показано, что производительность на
CRT немного увеличивается с участием исследования в целом и
в частности, предыдущее воздействие на ЭЛТ (Bialek & Pennycook, 2017; Haigh,
2016; Мейер, Чжоу и Фредерик, 2018; Stieger & Reips, 2016; Томсон и
Оппенгеймер, 2016).Однако в основном этот эффект наблюдается, когда люди
протестировано с тем же содержанием элемента (Chandler, Mueller & Paolacci,
2014; Finucane & Gullion, 2010; Hoover & Healy, 2017). Когда участники
представлены с похожими по структуре, но измененными по содержанию элементами (например,
«Журнал и банан в сумме стоят 2,20 доллара. Журнал стоит на 2 доллара дороже
чем банан. Сколько стоит банан? ») Ассоциация стремится
исчезают (Chandler et al., 2014; но см. также Meyer et al., 2018).
Было показано, что производительность на
CRT немного увеличивается с участием исследования в целом и
в частности, предыдущее воздействие на ЭЛТ (Bialek & Pennycook, 2017; Haigh,
2016; Мейер, Чжоу и Фредерик, 2018; Stieger & Reips, 2016; Томсон и
Оппенгеймер, 2016).Однако в основном этот эффект наблюдается, когда люди
протестировано с тем же содержанием элемента (Chandler, Mueller & Paolacci,
2014; Finucane & Gullion, 2010; Hoover & Healy, 2017). Когда участники
представлены с похожими по структуре, но измененными по содержанию элементами (например,
«Журнал и банан в сумме стоят 2,20 доллара. Журнал стоит на 2 доллара дороже
чем банан. Сколько стоит банан? ») Ассоциация стремится
исчезают (Chandler et al., 2014; но см. также Meyer et al., 2018).
В целом, немногочисленные доступные свидетельства, кажется, опровергают сильные
эффект спонтанного обучения при отсутствии инструкций или обратной связи.
Однако предыдущие исследования не всегда были специально разработаны для проверки
эффекты обучения и рассмотрены только ограниченное количество испытаний. Очевидно, тот факт, что люди не учатся после решения одной единственной
(или несколько) проблем не означает, что обучение невозможно
(Frensch & Runger, 2003). В настоящем исследовании мы стремимся предоставить более
окончательный тест в контролируемой экспериментальной обстановке.В течение часа
На тестовой сессии мы представили участникам 50 контент-модифицированных
предметы с битой и мячом и дополнительные проблемы контроля, чтобы проверить,
в конечном итоге сможет спонтанно изучить основную структуру
и избегайте предвзятых ответов.
Очевидно, тот факт, что люди не учатся после решения одной единственной
(или несколько) проблем не означает, что обучение невозможно
(Frensch & Runger, 2003). В настоящем исследовании мы стремимся предоставить более
окончательный тест в контролируемой экспериментальной обстановке.В течение часа
На тестовой сессии мы представили участникам 50 контент-модифицированных
предметы с битой и мячом и дополнительные проблемы контроля, чтобы проверить,
в конечном итоге сможет спонтанно изучить основную структуру
и избегайте предвзятых ответов.
Кроме того, мы также хотели изучить природу потенциального
эффект обучения. Недавно ряд исследований показал, что рассуждающие
кто правильно решает классические задачи рассуждения, часто может это сделать даже
когда обсуждение экспериментально сведено к минимуму (Bago & De Neys, 2017,
2019; Де Нейс, 2017; Ньюман, Гибб и Томпсон, 2017).Эти исследования
принять парадигму двух ответов (например, Thompson, Prowse-Turner &
Pennycook, 2011), в котором участники сначала должны ответить на
проблема с первым интуитивным ответом, который приходит в голову. Немедленно
после этого им дается все время, которое они хотят поразмышлять над
проблема и дать окончательный ответ. Чтобы свести к минимуму вероятность того, что
рассуждающие намеренно на этапе первоначального ответа, первый ответ
необходимо давать в условиях жесткой нехватки времени и / или когнитивной нагрузки, такой как
что у участников нет времени и ресурсов, чтобы заниматься
активное обсуждение (Bago & De Neys, 2017; Newman et al., 2017).
Результаты показывают, что люди, дающие правильный окончательный ответ после
обсуждение часто уже дал правильный ответ при первоначальном ответе
сцена.
Немедленно
после этого им дается все время, которое они хотят поразмышлять над
проблема и дать окончательный ответ. Чтобы свести к минимуму вероятность того, что
рассуждающие намеренно на этапе первоначального ответа, первый ответ
необходимо давать в условиях жесткой нехватки времени и / или когнитивной нагрузки, такой как
что у участников нет времени и ресурсов, чтобы заниматься
активное обсуждение (Bago & De Neys, 2017; Newman et al., 2017).
Результаты показывают, что люди, дающие правильный окончательный ответ после
обсуждение часто уже дал правильный ответ при первоначальном ответе
сцена.
В текущем исследовании мы приняли аналогичный дизайн с двумя ответами. В свободном
терминологии, мы хотели спросить, действительно ли в случае эффекта обучения
возникло в результате внезапного интуитивного озарения или более активного
обдумывание (или и то, и другое). Поэтому мы отслеживали, как повторная презентация
повлияли на точность начального и конечного отклика соответственно.Этот
также позволили нам проверить возможные эффекты автоматизации. Для
Например, участники могут давать предвзятые начальные и окончательные ответы в
начало исследования, при многократном воздействии они могут научиться
исправляются, когда дается достаточно времени для размышлений, и
затем, наконец, они могут научиться автоматизировать вычисления и начать
получение правильных первоначальных ответов.
Для
Например, участники могут давать предвзятые начальные и окончательные ответы в
начало исследования, при многократном воздействии они могут научиться
исправляются, когда дается достаточно времени для размышлений, и
затем, наконец, они могут научиться автоматизировать вычисления и начать
получение правильных первоначальных ответов.
2 Метод
2.1 Предварительная регистрация
Дизайн исследования и размер выборки были предварительно зарегистрированы в Open Science. Фреймворк (https: // osf.io / smqka / register / 5771ca429ad5a1020de2872e). Нет специальные анализы были предварительно зарегистрированы.
2,2 Участники
Мы набрали 62 участника (38 женщин, средний возраст = 35,5 лет, SD = 13,2).
лет) на Prolific Academic (https://www.prolific.ac). 1 Им заплатили 5 фунтов стерлингов за их
участие. Только носители английского языка из Канады, Австралии, New
Зеландия, Соединенные Штаты Америки или Соединенное Королевство разрешили
принять участие в исследовании. Среди них 35% (22 участника) сообщили о высоком
школа как высший уровень образования, а 62% (38 участников)
имели высшее образование и 3% (2 участника 14 и 19 лет)
сообщили, что их уровень образования ниже, чем в средней школе.
Среди них 35% (22 участника) сообщили о высоком
школа как высший уровень образования, а 62% (38 участников)
имели высшее образование и 3% (2 участника 14 и 19 лет)
сообщили, что их уровень образования ниже, чем в средней школе.
2.3 Материал
Всего было представлено 110 наименований. Сначала мы разработали 50 вариантов проблема с битой и мячом, имеющая ту же основную структуру, что и исходная проблема, но другое внешнее содержание элемента (например, «В Всего у жителей дома около 340 собак и кошек. Еще 300 собак чем кошки. Сколько там кошек? »). В каждой задаче указывалось два типа объекты с разным количеством вместо цен (например, см. Bago & De Нейс, 2019; Mata et al., 2017; Trouche, 2016). Каждая из 50 задач показывал уникальный контент с общим количеством, кратным десяти и варьировались от 110 до 650 (см. Приложение А).
Для каждой задачи предлагалось четыре варианта ответа; верное
ответ («5 центов» в оригинальной игре «битой и мячом»), интуитивно понятный
«Эвристический» ответ («10 центов» в исходной игре «бита и мяч») и два
варианты фольги. С математической точки зрения, правильное уравнение для решения
стандартная задача с битой и мячом: 100 + 2x = 110, вместо этого люди
считаются интуитивно понятными с помощью уравнения «100 + x = 110» для
определяют их реакцию (Канеман, 2011).Мы всегда использовали последнее
уравнение для определения «эвристического» варианта ответа, а первое — для
определить правильный вариант ответа для каждой проблемы. После Баго
и De Neys (2019), два варианта фольги всегда были суммой
правильный и эвристический ответ (например, «15 центов» в оригинальном слове «битой и мячом»)
единиц) и их второй по величине общий делитель (например, «1 цент» в
оригинальные единицы). Для каждого элемента четыре варианта ответа появились в
произвольно определенный порядок. Ниже показан весь элемент.
формат:
С математической точки зрения, правильное уравнение для решения
стандартная задача с битой и мячом: 100 + 2x = 110, вместо этого люди
считаются интуитивно понятными с помощью уравнения «100 + x = 110» для
определяют их реакцию (Канеман, 2011).Мы всегда использовали последнее
уравнение для определения «эвристического» варианта ответа, а первое — для
определить правильный вариант ответа для каждой проблемы. После Баго
и De Neys (2019), два варианта фольги всегда были суммой
правильный и эвристический ответ (например, «15 центов» в оригинальном слове «битой и мячом»)
единиц) и их второй по величине общий делитель (например, «1 цент» в
оригинальные единицы). Для каждого элемента четыре варианта ответа появились в
произвольно определенный порядок. Ниже показан весь элемент.
формат:
В доме у жителей 340 собак и кошек. общее.
Собак на 300 больше, чем кошек.
Сколько здесь кошек?
o 40
o 60
o 10
o 20
Одной из возможных причин отсутствия обучающего эффекта является то, что участники
просто надоедает повторная постановка задачи и прекращает
Уделение внимания. Чтобы избежать того, что задача станет слишком повторяющейся
и чтобы убедиться, что участники остаются минимально вовлеченными в задачу, мы
также построено 50 задач управления. В стандартной игре с битой и мячом
версии интуитивно запрограммированного «эвристического» ответа подсказывает ответ, который
противоречит правильному ответу.В «бесконфликтном» контроле
проблемы, эвристическая интуиция подсказывала правильный ответ
вариант. Это было достигнуто за счет удаления критического реляционного «more
чем »(например, De Neys, Rossi & Houdé, 2013; Travers et al.,
2016). В приведенном выше примере версия проблемы управления будет выглядеть как
следует:
Чтобы избежать того, что задача станет слишком повторяющейся
и чтобы убедиться, что участники остаются минимально вовлеченными в задачу, мы
также построено 50 задач управления. В стандартной игре с битой и мячом
версии интуитивно запрограммированного «эвристического» ответа подсказывает ответ, который
противоречит правильному ответу.В «бесконфликтном» контроле
проблемы, эвристическая интуиция подсказывала правильный ответ
вариант. Это было достигнуто за счет удаления критического реляционного «more
чем »(например, De Neys, Rossi & Houdé, 2013; Travers et al.,
2016). В приведенном выше примере версия проблемы управления будет выглядеть как
следует:
Всего в доме у жителей 340 собак и кошек.
Есть 300 собак.
Сколько кошек в доме?
o 40
o 60
o 10
o 20
В этом случае интуитивно понятный ответ «40» также был правильным.Мы
представлены те же четыре варианта ответа, что и для соответствующего стандарта
версия конфликта. Мы добавили три слова к вопросу о контрольной задаче
(например, «в здании»), чтобы стандартный «конфликт» и контроль
«Бесконфликтные» версии имели примерно одинаковую длину. Учитывая, что
элементы управления могут быть решены правильно на основе простой интуитивной
рассуждая, мы ожидали увидеть максимальную производительность по элементам управления
повсюду, если участники уделяют задаче минимальное внимание
и воздерживайтесь от простых случайных ответов.
Учитывая, что
элементы управления могут быть решены правильно на основе простой интуитивной
рассуждая, мы ожидали увидеть максимальную производительность по элементам управления
повсюду, если участники уделяют задаче минимальное внимание
и воздерживайтесь от простых случайных ответов.
Наконец, помимо наших 50 стандартных и контрольных элементов, мы также построили 10 задач-заполнителей, в которых участникам просто нужно было добавить две величины. Например,
В городе 30 пьющих пепси и 300 пьющих кока-колу.
Сколько всего пьющих кока-колы и пепси?
o 330
o 270
o 90
o 520
Мы посчитали, что проблемы с наполнителем могут еще больше помочь задача менее повторяющаяся и предсказуемая.
Всего участникам предстояло решить 110 задач.Проблемы были
сгруппированы в 10 блоков по 5 стандартных задач, 5 контрольных
проблемы, и одна проблема наполнителя. Проблема с наполнителем всегда была
представлена как шестая задача в блоке. Стандарт и контроль
задачи были представлены в рандомизированном порядке. Участники могли взять
небольшой перерыв после завершения каждого блока. Содержание стандарта
и проблемы управления в первом и последнем пяти блоках пересеклись.
Предметы, которые были представлены в стандартной версии в первой пятерке
блоки были представлены в бесконфликтной версии за последние пять
блоки и наоборот.Чтобы избежать эффекта знакомства, мы использовали то же
объектов, но с другим общим количеством для стандартных и
контрольный вариант задачи в первом и последнем наборе из 5 блоков.
Стандарт и контроль
задачи были представлены в рандомизированном порядке. Участники могли взять
небольшой перерыв после завершения каждого блока. Содержание стандарта
и проблемы управления в первом и последнем пяти блоках пересеклись.
Предметы, которые были представлены в стандартной версии в первой пятерке
блоки были представлены в бесконфликтной версии за последние пять
блоки и наоборот.Чтобы избежать эффекта знакомства, мы использовали то же
объектов, но с другим общим количеством для стандартных и
контрольный вариант задачи в первом и последнем наборе из 5 блоков.
2.4 Процедура
Эксперимент проводился онлайн на платформе Qualtrics. Участники были
специально проинструктировали, что исследование займет до одного часа и
требовали их полного внимания во всем. Мы приняли двухрежимный
процедура от Bago and De Neys (2017, 2019). Участники были проинструктированы
они должны были дать два последовательных ответа на каждую проблему.Они были
сказал, что мы были заинтересованы в их самом первом, первоначальном ответе, который пришел
в уме и были проинформированы, что после выбора первоначального ответа они
могли обдумать проблему и потратить столько времени, сколько им нужно, чтобы
дать окончательный ответ. Чтобы свести к минимуму вероятность того, что участники
продуманный на этапе первоначального реагирования, первоначальный ответ должен был
быть сгенерированным в течение строгого срока ответа и когнитивных
ресурсы были перегружены второстепенной задачей нагрузки. Крайний срок для
начальная реакция была установлена на 5 с, на основе предварительного тестирования Баго и Де
Neys (2019), который установил, что это время, необходимое для чтения
проблема.Задача загрузки была основана на задаче запоминания точек (Мияке,
Фридман, Реттингер, Шах и Хегарти, 2001). Перед каждой проблемой рассуждений
участникам был представлен сложный визуальный образец (например, 4 креста
в сетке 3×3) они должны были запоминать, решая рассуждения
проблема. После первого ответа на аргументную задачу
(интуитивно) участникам были показаны четыре разные матрицы, и они должны были
выберите правильный паттерн, который нужно запомнить (см. Приложение B). Загрузка
и крайний срок были применены только на этапе первоначального ответа, а не
на последующем этапе окончательного ответа, на котором участники
разрешено размышлять.
Чтобы свести к минимуму вероятность того, что участники
продуманный на этапе первоначального реагирования, первоначальный ответ должен был
быть сгенерированным в течение строгого срока ответа и когнитивных
ресурсы были перегружены второстепенной задачей нагрузки. Крайний срок для
начальная реакция была установлена на 5 с, на основе предварительного тестирования Баго и Де
Neys (2019), который установил, что это время, необходимое для чтения
проблема.Задача загрузки была основана на задаче запоминания точек (Мияке,
Фридман, Реттингер, Шах и Хегарти, 2001). Перед каждой проблемой рассуждений
участникам был представлен сложный визуальный образец (например, 4 креста
в сетке 3×3) они должны были запоминать, решая рассуждения
проблема. После первого ответа на аргументную задачу
(интуитивно) участникам были показаны четыре разные матрицы, и они должны были
выберите правильный паттерн, который нужно запомнить (см. Приложение B). Загрузка
и крайний срок были применены только на этапе первоначального ответа, а не
на последующем этапе окончательного ответа, на котором участники
разрешено размышлять.
После прочтения общих инструкций участники решили два не связанных между собой попрактиковаться в решении задач, чтобы ознакомить их с процедурой Следующий, они решили две задачи отзыва матрицы практики (без одновременных проблема рассуждения). Наконец, в конце практики им нужно было решить две предыдущие задачи практического мышления при когнитивной нагрузке. Они были затем напомнил, что нужно решить 110 проблем и что они могут делайте небольшую паузу после каждого блока из 11 задач.
Каждое испытание начиналось с показа креста фиксации на 2000 мс. Мы тогда представил первое предложение проблемы (например, «В Всего у жителей дома 340 собак и кошек ».) на 2000 мс. Затем был выбран целевой шаблон для задания на запоминание. представлены для 2000 мс. После этого была представлена полная проблема. В в этот момент участники должны были дать ответ 5000 мс; через 4000 мс фон экрана стал желтым, чтобы предупредить участников о приближающийся крайний срок. Если они не ответили до крайний срок, их попросили обратить внимание, чтобы дать ответ в течение крайний срок последующих испытаний.
После ввода первоначального ответа участникам были представлены четыре матричных шаблона, из которых они должны были выбрать правильный, запоминаемый образец. Как только они ответили на вопрос для запоминания, они получили отзывы о том, правильно ли это. Если бы ответ был не правильно, их также попросили уделять больше внимания запоминанию правильный образец при последующих испытаниях.
Наконец, тот же предмет был представлен снова, и участников спросили чтобы дать окончательный ответ.Порядок представления ответа варианты всегда были одинаковыми на этапе первоначального и окончательного ответа, но был рандомизирован по испытаниям. Как только участники щелкнули по одному из варианты ответа они автоматически переходили к следующему испытанию.
Цвет вариантов ответа был зеленым во время первого ответа, и синий во время финальной фазы ответа, чтобы визуально напомнить участникам на какой вопрос они отвечали. Поэтому прямо под вопрос, мы также представили предложение-напоминание: «Пожалуйста, укажите свой самый первый, интуитивный ответ.»И« Пожалуйста, дайте окончательный ответ », соответственно, которые также были выделены цветом как варианты ответа.
После каждого блока из 11 испытаний участникам сообщали, что они завершили блок и нужно было нажать кнопку, когда они были готовы перейти к следующему блоку. После пятого блока участники были напомнил, что они завершили половину исследования и были поощрены стараться оставаться максимально сосредоточенным до конца исследования.
В самом конце эксперимента участникам показали стандартную проблема с битой и мячом, и их спросили, видели ли они ее раньше.Мы также попросил их ввести раствор. Наконец, участники завершили страница с демографическими вопросами.
2,5 Критерии исключения
В общей сложности 26 участников сообщили, что видели проблему с битой и мячом. перед. Семнадцать из них (27,4% от всех участников) также предоставили правильный ответ «5 центов». Баго и Де Нейс (2019) исключили эти участников, чтобы исключить возможность того, что их предварительные знания исходное правильное решение повлияет на результаты.Текущий выводы были последовательными при анализе с применением и без применения исключение. Как заметил один рецензент, выраженная близость может просто быть плохим показателем для предшествующей разоблачения. Следуя рецензенту предложения, все представленные результаты относятся к полной выборке участники без исключения.
Участники не смогли дать свой первый ответ до крайнего срока на 117 испытаний (2% от всех испытаний), и в дальнейшем не удалось выбрать правильный матрица для задачи нагрузки по 543 испытаниям (9% от оставшихся испытаний).С мы не могли гарантировать, что первоначальный ответ на эти испытания не предполагая никаких обсуждений, мы отбросили их и проанализировали 5540 остальные испытания (89% от 6200). В среднем каждый участник внесло 44,5 (SD = 4,7) стандартных задач и 44,9 (SD = 4,7) контролировать бесконфликтные испытания.
Рис.1: Направление изменения классификации для каждого конфликтное испытание для каждого из 62 субъектов. («00», неправильный инициал и окончательный ответ; «11» — правильный начальный и окончательный ответ; «01», первоначальный неправильный и окончательный правильный ответ; «10», начальное правильное и окончательный неверный ответ).
3 Результаты и обсуждение
Чтобы узнать, происходит ли и какой тип обучения, мы рассмотрели, как участники меняли или не меняли свои ответы на протяжении всего исследование путем проведения анализа направления изменений (Bago & De Neys, 2017, 2019). Более конкретно, в каждом испытании люди могут дать правильный или неправильный ответ на каждом из двух этапов ответа. Следовательно, в теории, это может привести к четырем различным типам ответов на любое отдельное испытание («00», неправильный ответ на обоих этапах; «11», правильный ответ на обоих этапах; «01», неверное начальное и окончательное правильный ответ; «10», первоначальный правильный и окончательный неправильный ответ).На рисунке 1 показана классификация направлений изменений для каждой из 50 критические конфликтные испытания для каждого отдельного участника. 2 Наблюдая за цифрой 1 балл к следующим описательным тенденциям:
Во-первых, подавляющее большинство участников (n = 38 из 62, 61%) в основном давал 00 ответов на протяжении всего исследования. Эти участники обозначены как «предвзятая» группа на рисунке 1. Оба их первоначальная догадка и окончательный осознанный ответ обычно были неверными от начала до конца.Следовательно, даже после очень обширных повторных разоблачения, большинство участников не смогли решить проблему с битой и мячом на конец исследования. Само по себе это, кажется, подтверждает доказательства против сильного эффекта спонтанного обучения в предыдущих исследования с более ограниченным количеством исследований.
Во-вторых, 10 участников (из 62, 16%) начали с одного или нескольких 00 ответов, но затем, похоже, через пару испытания и в большинстве случаев правильно ответили впоследствии. Эти участники обозначены как «группа понимания» на Рисунке 1.Следовательно, для этой небольшой группы есть свидетельства спонтанного обучения или эффект устранения смещения, возникающий в результате простого повторения презентации. это примечательно, что понимание обычно происходило в начале исследования. (т.е. всегда до суда 20 и часто раньше). Более того, есть также свидетельство быстрой автоматизации правильного решения стратегия. В большинстве «инсайдерских» случаев за испытаниями 00 следуют просто единственное испытание 01, после которого испытуемые преимущественно давали 11 ответы. Следовательно, понимание обычно происходило во время фаза обдумывания, но этого было достаточно для решения последующих проблем правильно во время начальной фазы ответа.
В-третьих, 14 участников (из 62, 23%) начали с правильной оценки. окончательный ответ по первому испытанию и обычно продолжал отвечать правильно до конца. Эти участники обозначены как «Правильная» группа на Рисунке 1. Меньшинство в этой группе начало дали 11 ответов с самого начала (5 из 14, 36%), но большинство правильные респонденты начали как минимум с одного ответа 01, после чего они быстро дали 11 ответов. Следовательно, как в «прозрении» group мы видим свидетельства быстрого процесса автоматизации.Один или два испытания, в которых правильный ответ генерируется после обсуждения достаточно, чтобы вызвать правильный ответ в качестве первоначальной догадки после.
3.1 Дополнительный анализ
Помимо 50 конфликтных проблем, участники также решили 50 контроль, бесконфликтные проблемы. Показатели на бесконфликтных испытаниях были постоянно на потолке на протяжении всего исследования (средний начальный ответ = 96,6%, SD = 18,3%; средний окончательный ответ = 99%, SD = 10%). Это может помочь спорить против возможной общей путаницы.Одно объяснение отсутствие сильного эффекта смещения будет заключаться в том, что длительный характер учеба просто заставила большинство участников отвлечься от задачи и отвечать случайным образом без обработки материала. Однако потолок производительность по контролю бесконфликтных задач указывает на то, что участники уделяли минимум внимания и хотя бы дочитали задачи до конца исследования.
Наш главный интерес в данном исследовании касался точности отклика. Для полноты картины заинтересованный читатель может найти дополнительные исследовательские анализирует изменения в обнаружении конфликтов и типах неправильный ответ в исследовании в Приложении C.
4 Обсуждение
Наши результаты показывают, что обширное повторное воздействие в целом ограниченное влияние на игру участников в игре с битой и мячом проблема. Для большинства участников как первые догадки, так и ответы, которые они давали после обсуждения, были преимущественно предвзятыми начать заканчивать. Даже после решения до 50 стандартных задач, обычно преобладает эвристический ответ. В то же время обучение было не полностью отсутствует. Небольшая группа изначально предвзятых мыслителей пришел к пониманию после некоторых испытаний и правильно ответил впоследствии.Интересно, что были доказательства типа быстрой автоматизации правильная стратегия решения. В то время как понимание обычно происходило во время обдумывания почти сразу же были устранены последующие проблемы. (т.е. после одного или двух испытаний) решено правильно во время начального фаза ответа. Такая же быстрая автоматизация наблюдалась среди правильные респонденты, исправившие начальную ошибку при первом испытание (я). Единичный случай правильного ответа после обдумывания часто бывает достаточно, чтобы дать правильные первоначальные ответы на последующие проблемы.
Хотя мы не оспариваем, что обучение в целом было редкостью, мы верим что случаи «автоматизации», в которых это действительно происходило, вполне замечательный. Во всех тех случаях, когда люди приходили к правильному ответ на этапе обсуждения, они мгновенно сумели сгенерировать правильный ответ на следующем этапе начального ответа (т. е. во время которые экспериментально сведены к минимуму). Можно задаться вопросом, что лежит в основе этого процесса автоматизации: учатся ли люди автоматизировать лежащее в основе математическое уравнение (например,g., «X + Y = 1,10, Y = 1 + X, Решите для X ») или они скорее научатся применять более простое решение правило (например, «взять половину эвристического ответа»). Наше исследование не было предназначены для решения этой проблемы, но учтите, что даже если люди просто с применением решающего правила это далеко не тривиально. Во-первых, помните, что мы использовали задачи с измененным содержанием с разным количеством. Следовательно, люди не могут просто повторять предыдущий правильный ответ (например, «Всегда 5 центов»). Во-вторых, слепое применение «взять половину» Правило повсюду привело бы к ошибкам при решении задач управления.Следовательно, участникам необходимо как минимум различать контроль и стандартные задачи и признать, что правило принятия решения подходит для решающей проблемы. В-третьих, участникам нужны структурные понимание возможности обобщения принципа «взять половину» и поймите, что правило не привязано к конкретным значениям в проблема. Например, если эвристический ответ составляет 10 центов и правильный ответ 5 центов, участники должны правильно оценить, что правильный ответ на последующие проблемы требует вдвое уменьшения эвристики ответ вместо вычитания «5 центов».В общем, наша точка зрения состоит в том, что даже применение упрощенного правила принятия решений требует некоторых минимальное математическое понимание структурных отношений между проблемные значения. Хотя мы еще раз подчеркиваем, что это явление редко в абсолютном выражении, и что большинство рассуждающих остаются предвзятыми повсюду, он заслуживает внимания и заслуживает большего внимания со стороны предвзятость исследователей в будущей работе.
В этом исследовании мы предложили участникам всего 110 задач. Кто-то может возразить, что нельзя исключать более сильного спонтанного эффект обучения будет иметь место при более длительной программе воздействия, в которой было представлено больше проблем.Мы считаем это маловероятным. Во-первых, Настоящее исследование заняло около часа. Продвигать мыслителей еще дальше — это очень вероятно, что это приведет к эффектам усталости, которые просто сделают участники отключаются от задачи. Во-вторых, в исследовании представлены как стандартные и контрольные задачи. Утверждалось, что такой внутрипредметная презентация может помочь привлечь внимание участников к переменная или характеристика критической проблемы (Kahneman & Fredrick, 2005). В этом смысле наш дизайн задачи уже создал оптимальные условия. для спонтанного обучения.В-третьих, как показано на рисунке 1, в в этих случаях понимание действительно происходило, обычно это происходило в самом начале а не конец исследования, предполагая, что добавление дополнительных испытаний мало повлияет. Поэтому мы считаем, что безопасно сделать вывод, что простое продление сеанса тестирования не приведет к изменили (то есть улучшили) результаты.
Настоящее исследование сосредоточено на влиянии экспериментально манипулируемых многократное воздействие на выполнение задачи с битой и мячом. Общий ограниченный доказательства эффекта спонтанного обучения согласуются с предыдущими исследованиями, которые изучили влияние естественных вариаций воздействия бита и мяч и / или связанные проблемы из теста когнитивной рефлексии (ЭЛТ, эл.г., Bialek & Pennycook, 2017; Chandler et al., 2014). Обратите внимание, что эти предыдущие исследования часто также интересовались влиянием повторяющихся воздействие на прогностическую достоверность ЭЛТ (например, корреляция между оценкой CRT и, например, восприимчивостью к эвристике и предубеждения, например, Bialek & Pennycook, 2017). Настоящее исследование не рассматривало это вопрос действительности.
В заключение мы хотели бы особо подчеркнуть, что настоящее исследование не означает, что невозможно научиться избегать предвзятого рассуждения.По методологическим причинам нас интересовали спонтанные обучение без инструкций или обратной связи. Очевидно, это не подразумевают, что бесполезно пытаться спланировать вмешательство или устранить предвзятость обучающие программы. Например, предыдущая работа уже указала, что должным образом проинструктировать людей о математическом уравнении, лежащем в основе может помочь повысить производительность в задаче с мячом и битой (Hoover & Хили, 2017). Следовательно, дело не в том, что люди не могут научиться рассуждайте правильно. Дело в том, что большинство людей будут делать это редко. самопроизвольно, когда ему неоднократно сталкиваются с одной и той же проблемой.
Ссылки
Bago, B., & De Neys, W. (2017). Быстрая логика ?: Изучение хода времени предположение теории двойственных процессов. Познание, 158, 90–109.
Баго Б. и Де Нейс В. (2019). Интеллектуальная система 1: доказательства интуитивный характер правильного ответа на задачу о бита и мяча. Мышление и рассуждение. http://dx.doi.org/10.1080/13546783.2018.1507949.
Баго Б., Раоэлисон М. и Де Нейс В. (2019). Второе предположение: тестирование специфика обнаружения ошибок в задаче о биту и мяче.Acta Psychologica, 193, 214–228.
Биалек, М., и Пенникук, Г. (2018). Тест на когнитивную рефлексию устойчив к многократным воздействиям. Методы исследования поведения, 50 (5), 1953–1959.
Чандлер Дж., Мюллер П. и Паолаччи Г. (2014). Ноннаиве среди amazon Mechanical turk worker: Последствия и решения для поведенческие исследователи. Методы исследования поведения, 46 (1), 112–130.
Де Нейс, В. (Ред.). (2017). Теория двойного процесса 2.0. Лондон: Рутледж.
Де Нейс, В., Росси, С., & Худе, О. (2013). Летучие мыши, мячи и Чувствительность к замещению: скупые когнитивные люди — не счастливые дураки Психономический бюллетень и обзор, 20 (2), 269–273.
Finucane, M. L., & Gullion, C. M. (2010). Разработка инструмента для измерение способности пожилых людей принимать решения. Психология старения, 25 (2), 271–288.
Фредерик, С. (2005). Когнитивное размышление и принятие решений. Журнал экономических перспектив, 19 (4), 25–42.
Frensch, P. A., & Rünger, D.(2003). Неявное обучение. Текущий Направления психологической науки, 12 (1), 13–18.
Гангеми, А., Буржуа-Жиронда, С., и Манчини, Ф. (2015). Чувства ошибка в рассуждении — поиск явления. Мышление и Рассуждение, 21 (4), 383–396.
Хей, М. (2016). Стал ли стандартный тест на когнитивную рефлексию жертва собственного успеха? Достижения в когнитивной психологии, 12 (3), 145.
Гувер, Дж. Д., и Хили, А. Ф. (2017, декабрь). Алгебраические рассуждения и Варианты задачи с битой и мячом: сначала решить изоморфную алгебру облегчает решение проблем позже.Психономический бюллетень и Обзор, 24 (6), 1922–1928.
Джонсон, Э. Д., Тубау, Э., и Де Нейс, В. (2016). Система сомнений 1: Доказательства чувствительности к автоматической замене. Acta психология, 164, 56–64.
Канеман Д. (2002). Карты ограниченной рациональности: взгляд на интуитивное суждение и выбор. Лекция о Нобелевской премии, 8, 351–401.
Канеман Д. (2011). Думаю, быстро и медленно. Нью-Йорк: Фаррар, Штраус и Жиру.
Канеман Д. и Фредерик С.(2005). Модель эвристического суждения. В К. Холиоак и Б. Моррисон (ред.), Кембриджский справочник мышление и рассуждение (стр. 267–293). Издательство Кембриджского университета.
Кориат А. (2017). Могут ли люди идентифицировать «вводящие в заблуждение» или «вводящие в заблуждение» предметы которые дают в основном неправильные ответы? Журнал Принятие поведенческих решений, 30 (5), 1066–1077.
Мата, А., Феррейра, М. Б., Восс, А., и Коллей, Т. (2017). Видя конфликт: внимательное рассмотрение ошибок рассуждения. Психономический бюллетень и обзор, 24 (6), 1980–1986.
Мейер А., Чжоу Э. и Фредерик С. (2018). Отсутствие последствий многократное прохождение теста на когнитивную рефлексию. Суждение и принятие решений, 13 (3), 246–259.
Мияке А., Фридман Н. П., Реттингер Д. А., Шах П. и Хегарти М. (2001). Как работают зрительно-пространственная рабочая память, исполнительные функции и пространственные способности связаны? анализ скрытых переменных. Журнал экспериментальной психологии: General, 130 (4), 621.
Newman, I. R., Gibb, M., & Thompson, V.А. (2017). Рассуждения, основанные на правилах быстро, а рассуждения, основанные на убеждениях, могут быть медленными: бросая вызов текущим объяснения предвзятости веры и пренебрежения базовой ставкой. Журнал экспериментальная психология. Обучение, память и познание, 43 (7), 1154–1170.
R Основная команда. (2017). R: язык и среда для статистических вычисления. R Фонд статистических вычислений, Вена, Австрия. URL https://www.R-project.org/
Стагнаро, М. Н., Пенникук, Г., и Рэнд, Д. Г. (2018). Производительность на Когнитивная рефлексия стабильна во времени.Суждение и принятие решений, 13 (3), 260–267.
Стюарт, Н., Чендлер, Дж., И Паолаччи, Г. (2017). Примеры краудсорсинга в когнитивной науке. Тенденции в когнитивных науках, 21 (10), 736–748.
Stieger, S., & Reips, U.-D. (2016). Ограничение познавательного тест на отражение: знакомство. PeerJ, 4, e2395.
Соллози, А., Баго, Б., Сасзи, Б., и Акзель, Б. (2017). Изучение детерминанты уверенности в проблеме биты и мяча. Acta Psychologica, 180, 1–7.
Томпсон, В. А., и Джонсон, С. С. (2014). Конфликт, метапознание и аналитическое мышление. Мышление & Рассуждение, 20 (2), 215–244.
Томпсон, В. А., Тернер, Дж. А. П., и Пенникук, Г. (2011). Интуиция, разум и метапознание. Когнитивная психология, 63 (3), 107–140.
Томсон, К. С., & Оппенгеймер, Д. М. (2016). Изучение альтернативного форма теста на когнитивную рефлексию. Суждение и решение Изготовление, 11 (1), 99–113.
Трэверс, Э., Ролисон, Дж. Дж., И Фини, А. (2016). Курс времени конфликта на тесте когнитивной рефлексии. Познание, 150, 109–118.
Trouche, E. (2016). Рассуждения как социальная компетентность: экспериментальное сравнение с интеллектуалистскими теориями (Тезисы, Лионский университет).
Приложение A. Обоснование
Разъяснение конструкции материала.
Объекты, которые мы использовали для создания задач, были получены из 10 категории (животные, фрукты, посуда, инструменты, группы людей, заводы, профессии, спорт, инструменты и транспортные средства), с каждым блоком содержащий по одной паре объектов каждой категории.Первый набор из пяти блоки использовали стандартные задачи, полученные из первых пяти категорий и проблемы управления из последних пяти. Этот шаблон был отменен для последнего набора из пяти блоков. Общее количество колебалось от 110 и 650 и всегда было кратным десяти (значения 200, 300, 400, 500 и 600 были исключены).
Содержание стандартных и контрольных задач в первой и последней пять кварталов было пересечено. Предметы, представленные в их стандарте версии в первых пяти блоках были представлены в их неконфликтных версия в последних пяти блоках и наоборот.Чтобы уменьшить знакомство эффекты, стандартные и уравновешенные версии управления используются одинаково содержание объекта, но указано другое общее количество.
Блок-конструкция и презентация.
В каждом блоке было по два мини-набора, по 3 стандартных и 2 контрольных. проблемы, или 2 стандартные и 3 контрольные задачи, помимо наполнителя проблема, которая всегда возникала между мини-наборами (т.е. шестая позиция). Порядок представления мини-наборов был рандомизировано для каждого участника.Проблемы внутри мини-набора тоже были представлены случайным образом.
Итого 10 основных блоков (по 11 задач в каждом), которые сгенерированные нами были представлены в четырех возможных блоках: a. блокировать 1–5, корп. 6–10, стр. блок 1–5, блок 10–6, c. блок 5–1, блок 6–10, д. блок 5–1, блок 10–6.
Пример блока.
Вот иллюстрация последовательности задач в блоке:
- Всего в компании 150 мужчин и женщин.
Мужчин на 100 больше, чем женщин.Сколько там женщин?
50/5/25/75
- Научная ярмарка собрала 440 изобретателей и инженеров.
Есть 400 изобретателей. Сколько инженеров в этой науке Справедливая?
10/40/20/60
- Всего на кухне 260 ножей и ложек.
Ножей на 200 больше, чем ложек. Сколько там ложек?
90/30/60/15
- Всего город приобрел 610 автобусов и поездов.
Всего 600 автобусов.Сколько поездов в этом городе?
1/15/5/10
- В магазине можно выбрать между 320 помидорами и авокадо.
Помидоров на 300 больше, чем авокадо. Сколько там авокадо?
30/5/10/20
- В городе 30 пьющих пепси и 300 пьющих колу.
Сколько всего пьющих кока-колы и пепси?
270/90/330/520
- В национальном парке всего 380 роз и цветов лотоса.
Всего 300 роз.Сколько цветов лотоса в этом парке?
40/20/80/120
- Всего в доме у жителей 370 собак и кошек.
Собак на 300 больше, чем кошек. Сколько там кошек?
35/7/70/105
- Всего в музыкальном магазине 210 саксофонов и флейт.
Саксофонов на 200 больше, чем флейт. Сколько там флейт?
5.10.15/1
- На стадионе 490 волейболистов и бейсболистов.
Есть 400 волейбольных.Сколько бейсболистов в стадион?
15/90/135/45
- Всего в магазине 550 гвоздей и молотков.
Есть 500 гвоздей. Сколько молотков в этом магазине?
50/75/5/25
Полный список проблем.
Полный список используемых предметов доступен в Материалы.
Приложение Б. Расчет матриц нагрузок
Шаблоны были разработаны с использованием функции комбинирования в R (R Core Команда, 2017).Поскольку каждая сетка 3×3 содержала четыре креста, мы использовали combn (9,4), чтобы перечислить все возможные комбинации и расположенные кресты соответственно. Для стандартных и контрольных задач мы исключили шаблоны. считается слишком легким для запоминания, например, те, которые содержат три креста на вертикальная, горизонтальная или диагональная линия. Однако эти шаблоны, которые легче запомнить, все еще можно было использовать в качестве отвлекающих факторов и также используется в качестве целевых шаблонов для проблем с наполнителем.
На этапе ответа участникам были представлены четыре матрицы шаблоны, из которых они должны были выбрать правильные, которые нужно было запомнить шаблон.Неправильные (отвлекающие) паттерны систематически построен. Первым отвлекающим фактором был следующий паттерн в нашем сгенерированном R list, что означает, что он разделяет три креста с целевым рисунком. В второй был «дополнительным» узором, не имевшим ничего общего с крестиком. целевой шаблон. Наконец, третьим отвлекающим фактором был паттерн, который последовал за вторым отвлекающим фактором в списке. Рисунок 1 иллюстрирует процесс построения выкройки. Все материалы нашего задания могут быть получено с нашей страницы OSF (https: // osf.io / 6aec3 /).
Рисунок S1. Пример различных вариантов ответа в загрузке матричная задача: правильный ответ, затем три отвлекающих фактора.
Приложение C. Дополнительные анализы
Наш основной теоретический интерес к настоящему исследованию касался человеческих точность отклика. В целом, наши выводы о точности показали ограниченное доказательства сильного обучающего эффекта. Однако не исключено, что там могут быть более тонкие обучающие эффекты под поверхностью точности. Для Например, предыдущая работа показала, что предвзятые респонденты в борьбе с битой и мячом проблема часто показывает некоторую минимальную чувствительность к ошибкам (например,г., Де Нейс и др., 2013; Гангеми, Буржуа-Жиронда и Манчини, 2015; Джонсон, Тубау и Де Нейс, 2016; Кориат, 2017). Участники сомневаются в правильности своих ответы с битой и мячом, что отражается в более низкой уверенности ответа и более время реакции при реагировании на стандартный или бесконфликтный контроль проблемы. Однако не все предвзятые аргументы демонстрируют это «обнаружение конфликта». эффект (например, Frey, Johnson & De Neys, 2017; Mata, Ferreira, Voss & Коллей, 2017; Szollosi, Bago, Szaszi & Aczel, 2017; Трэверс, Ролисон и Фини, 2016).Возможно, повторное воздействие увеличивает вероятность этого. чтобы предвзятые мыслители подхватили конфликт и тем самым повысили эффект. Как и в предыдущих исследованиях по обнаружению ошибок или систематических ошибок (например, Johnson et al. al., 2016), поэтому мы рассчитали индекс обнаружения конфликтов на основе задержки ответа участников (т. е. задержка ответа на неверный ответ на стандартную проблему за вычетом задержки ответа для правильного ответа на проблема управления. 3 ). При сопоставлении индекса по в различных исследованиях наблюдалась общая описательная тенденция к снижение эффекта при повторном предъявлении. Это наблюдалось как для окончательный ответ (первое испытание: M = 689 мс, SD = 3697 мс vs последнее испытание: M = 358 мс, SD = 2078 мс) и исходный. 4 ответ (первое испытание: M = 316 мс, SD = 1180 мс, по сравнению с последним испытанием: M = -23 мс, SD = 833 мс). Следовательно, если что-либо имелось доказательств эффект привыкания. Многократная презентация, казалось, вызвала предвзятость менее реагирует на наличие конфликта.
Наконец, мы исследовали, изменился ли тип неправильного ответа через учеба. То есть мы всегда предъявляли участникам четыре ответа варианты: правильный ответ (например, «5 центов»), эвристический ответ (например, «10 центов »), и два неправильных ответа фольгой (например.г., «1 цент» и «15 центов »). Мы просто исследовали, были ли какие-либо изменения в типе неправильный ответ в различных испытаниях (например, были ли аргументы меньше привлекает эвристический ответ ближе к концу исследования?). Тем не мение, на протяжении всего исследования преобладающий неправильный ответ на стандарт проблемы всегда были эвристическим вариантом ответа [первоначальный ответ: первое испытание: M = 94,9%, SD = 22,2%; последнее испытание: M = 94,9%, SD = 22,2%; окончательный ответ: первое испытание: M = 100%, SD = 0; последнее испытание: M = 98%, SD = 14.1%]. Постоянно высокая распространенность одного конкретного тип ошибочного ответа дополнительно указывает на то, что общая низкая точность не является результатом общей тенденции отвлекаться от задачи и ответить случайным образом.
Этот документ был переведен с L A T E X пользователем H E V E A .
Простой логический вопрос, который ошибается большинством студентов Гарварда
студентов Хаварда получают почти идеальные результаты по SAT.Это умные, умные дети. Значит, у них не должно возникнуть проблем с простым логическим вопросом, верно?
Решите следующую загадку:
Бита и мяч стоят 1,10 доллара.
Бита стоит на доллар больше, чем мяч.
Сколько стоит мяч?
Прокрутите вниз, чтобы найти ответ…
Фото: theseanster93 через www.flickr.com Creative Commons
Вы, наверное, ответили 10. Так ответило большинство студентов Гарварда.Но настоящий ответ — 5 центов.
Поведенческий экономист Дэниел Канеман объясняет, почему большинство людей ошибаются:
Вам пришло в голову число. Число, конечно же, 10: 10 ¢. Отличительной чертой этой легкой головоломки является то, что она вызывает интуитивный, привлекательный и неправильный ответ. Посчитайте, и вы увидите. Если мяч стоит 10 центов, общая стоимость составит 1,20 доллара (10 центов за мяч и 1,10 доллара за биту), а не 1,10 доллара. Правильный ответ — 5 центов. Можно с уверенностью предположить, что интуитивный ответ пришел в голову и тем, кто в итоге набрал правильное число — им каким-то образом удалось противостоять интуиции.
Многие тысячи студентов университетов ответили на головоломку с битой и мячом, и результаты шокируют. Более 50% студентов Гарварда , Массачусетского технологического института и Принстона дали интуитивный — неправильный — ответ. В менее отобранных университетах процент очевидных отказов в проверке превышал 80%. Проблема с битой и мячом — это наша первая встреча с наблюдением, которое будет постоянной темой этой книги: многие люди слишком самоуверенны, склонны слишком сильно доверять своей интуиции.Очевидно, они находят когнитивное усилие, по крайней мере, слегка неприятным, и избегают его по мере возможности.
Этот отрывок взят из книги Канемана 2011 года «Мышление, быстро и медленно», в которой утверждается, что у нас есть интуитивная ментальная система и логическая ментальная система, и мы часто используем неправильную в неподходящее время.
НЕ ПРОПУСТИТЕ: 61 поведенческое предубеждение, портящее ваше мышление
Электронные письма и оповещения Business Insider
Сайт освещается каждый день на ваш почтовый ящик.
Следите за подпиской Business Insider Australia в Facebook, Twitter, LinkedIn и Instagram.
Стоимость бейсбольной биты и мяча 1,10: объяснение ответа на загадку
Многие пытаются разгадать «загадку стоимости бейсбольной биты и мяча 1,10». Не можете понять? Не волнуйтесь, у нас есть ответ .
Во время изоляции мы обратились к нескольким вещам, чтобы занять себя и развлечься.
Для большинства из нас стало больше садоводства, кулинарии, фильмов, телевидения и упражнений, но неожиданно загадок появилось намного больше.
За последние пару месяцев многие зашли в социальные сети, чтобы поделиться множеством загадок со своими друзьями, семьей и последователями. Некоторые из них были изобретены недавно, тогда как самые лучшие — это возродившаяся классика.
Они предоставили изящный способ дать нашему мозгу быструю тренировку, но этот последний совершенно сбил с толку…
- ИСТОРИЯ : Джастин Сэлинджер сияет в Гранте
Бейсбольная бита и мяч стоят 1.10 загадок
Хорошо, давайте погрузимся в загадку:
Бита и мяч в сумме стоят 1,10 доллара. Бита стоит на 1 доллар дороже мяча. Сколько стоит мяч?
Хорошо подумайте, прежде чем переходить к ответу; найдите время, чтобы сломать это.
Еще нет?
Ну, не волнуйтесь. Спуститесь вниз за ответом.
Этот контент не может быть загружен
Бита и мяч стоят 1 доллар.10.
Бита стоит на доллар больше, чем мяч.
Сколько стоит мяч?[Остерегайтесь ленивого мышления] 🙂
— Pretheesh (@ Pretheesh21) 31 мая 2020 г.
Вот ответ
Ответ на загадку «бита и мяч» — 5 центов.
Многие ответят 10, что неверно. Поясним…
Если бита стоит на 1 доллар больше, чем мяч, а общая сумма составляет 1,10 доллара, то мяч должен стоить 5 центов, а бита — 1 доллар.05.
Если бы мяч стоил десять центов, то оба вместе стоили бы 1,20 доллара.
Это непростой вопрос, поскольку большинство людей читают его так, как будто летучая мышь стоит один доллар.
Убедитесь, что ваша семья и друзья смогут его взломать! А пока у нас есть еще одна загадка, которую вы можете попробовать:
«Что можно увидеть в середине марта и апреля, чего нельзя увидеть в начале или в конце каждого месяца?»
Из других новостей, поклонников Люцифера повезло.
Сможете ли вы решить эту проблему? Летучая мышь, мяч и обман | Математика
Вот известная головоломка:
Бита и мяч стоят 1,10 фунта стерлингов. Бита стоит на 1 фунт больше, чем мяч. Сколько стоит мяч?
Головоломка хорошо известна, потому что люди часто ошибаются, хотя арифметические операции очень просты. На ум приходит «мгновенный» ответ: мяч стоит 10 пенсов. Фактически, после минутного размышления, ответ очевиден: 5 пенсов.(Таким образом, летучая мышь стоит 1,05 фунта стерлингов.)
Шесть сегодняшних головоломок похожи на них. Один ответ напрашивается сразу. Однако часто этот ответ неверен. Однако, прежде чем вы начнете слишком дерзко, один из приведенных ниже вопросов был задан 185 студентам Гарвардского университета, и все они ошиблись.
1. Если пяти эльфам требуется пять минут, чтобы обернуть пять подарков, сколько времени потребуется пятидесяти эльфам, чтобы обернуть пятьдесят подарков?
2. Матери и дочери всего пятьдесят лет.Мать старше дочери на 20 лет. Сколько лет дочери?
3. Сколько людей три тройки тройняшек трижды?
4. Если подбросить монету 3 раза, какова вероятность подбросить хотя бы 2 головы?
5. Сегодня утром 100 кг кабачков бросили на солнце. Они на 99% состояли из воды, но в течение дня теряли влагу из-за испарения, и теперь они состоят только из 98% воды. Сколько они сейчас весят?
6.Если я дал вам 100 фунтов стерлингов сегодня, а вы возвращали мне 10 фунтов стерлингов каждый месяц в течение года, какова будет годовая процентная ставка по вашему кредиту?
Идея сегодняшних головоломок пришла от Тима Харфорда, чья своевременная и блестяще читаемая новая книга «Как заставить мир складываться» является манифестом, демистифицирующим числа. Если использовать подходящую метафору, в этой книге он выбивает мяч из парка!
«Люди всегда просят меня проверить статистику, но многие статистические утверждения похожи на эти головоломки: мы автоматически переходим к выводу», — говорит Харфорд.«Итак, прежде чем мизинец нажать на кнопку« ретвитнуть »или« поделиться »… остановись и подумай!»
Спасибо также Шейну Фредерику, профессору из США, которого я упомянул выше, все студенты Гарварда ответили на один из вопросов неправильно. (Он также поставил ту же задачу для студентов MBA Йельского университета, и они не справились намного лучше.) В 2005 году Фредерик создал тест на когнитивную рефлексию, список вопросов — включая вопрос «бита и мяч» — с неправильным «чутьем». отклик. Загадки выше вдохновлены его тестом.
Я вернусь в 17:00, чтобы дать ответы и обсудить результаты.
ПОЖАЛУЙСТА, НЕ СПОЙЛЕРЫ. Однако, пожалуйста, разместите свои любимые вопросы в стиле «бита и мяч» под линией.
ОБНОВЛЕНИЕ: Решения уже доступны, их можно прочитать здесь.
ОБНОВЛЕНИЕ 2: Изначально в этом посте была форма для отправки, в которую вы могли вставить свои ответы. Теперь я закрыл эту форму, так как она была действующей только до тех пор, пока решения не были напечатаны. Вы можете прочитать результаты того, насколько хорошо все сделали, в сообщении о решении.
Я задаю здесь головоломку каждые две недели в понедельник. Я всегда ищу отличные головоломки. Если вы хотите предложить один, напишите мне.
Из других интересных новостей, осталось всего две недели до издательского события года, выпуска моей новой книги! Книга-головоломка для любителей языков посвящена миру слов и языка и включает проблемы, связанные с древними, современными и изобретенными языками, любопытными алфавитами и системами письма, сленгом, искусственным интеллектом и многим другим.Дэвид Кристал называет это: «Идеальный компаньон для всех, кто любит головоломки и языки». Кто я такой, чтобы не согласиться! Книга выйдет 5 ноября, но вы можете оформить предзаказ в книжном магазине Guardian.
Источники сегодняшних головоломок: 1. Традиционные. 2. Эндрю Мейер и Шейн Фредерик. 3 Традиционный. 4 Шейн Фредерик. 5. Традиционный. 6 Шейн Фредерик через Виктора Станго и Джонатана Зинмана.
Ответ на загадку здесь
Сколько стоит мяч?Я читаю книгу Дэна Гарднера «Риск».В книге «Риск» есть загадка. Это битой и мяч вопрос . Автор, Дэн Гарднер, говорит, что у нас есть два пути решения проблем и то, что мы в конечном итоге скажем.
System One и System Two , по-видимому, то, что мы используем для решения головоломок. Загадка с битой и мячом проверяет эти две психологические системы. Решил вопрос «сколько стоит мяч?».
Можете ли вы решить это сами, прежде чем увидите ответ ниже 🙂
Тест на когнитивную рефлексию «Летучая мышь и мяч»
Бита и мяч стоят 1 доллар.10
Если бита стоит на 1 доллар больше мяча, то сколько стоит мяч?
Самый распространенный и ответный ответ — это, вероятно, то, что вы только что сказали вслух или в уме.
Да, наиболее распространенный ответ на то, сколько стоит мяч, — это 10 центов .
Однако вы ошибаетесь , если вы ответили 10 центов.
Как это может быть, спросите вы? Ну, это тип теста IQ, помните. Вы найдете ответ на викторину с битой и мячом в конце этого поста.
А пока быстро прокрутите вниз и дайте мне знать, какой вы думаете ответ и почему, в разделе комментариев ниже.
Правильный ответ
Викторина с битой и мячом — это тест интеллекта, который был разработан Шейном Фредриком из Массачусетского технологического института. Это проверка того, какой тип мышления вы в основном используете. Либо быстро с небольшим осознанным обдумыванием , либо медленнее и более рефлексивно .
Вот как Шейн объясняет, почему он придумал загадку:
Помните пословицу о доверии своему первому инстинкту? Забудьте об этом, — говорит профессор Слоуна из Массачусетского технологического института Шейн Фредерик, который разработал простой тест из трех пунктов, который измеряет способность людей сопротивляться своему первому инстинкту.
«Вы хотите, чтобы кто-то руководил вашей компанией, который не мыслил дальше своего первого импульса, — спрашивает Фредерик, — или вы хотите кого-то, кто готов спросить себя:« Имеет ли этот ответ какой-то смысл? »» Он говорит, что тест на когнитивную рефлексию служит приблизительной оценкой этой способности или предрасположенности.
Профессор Слоуна из Массачусетского технологического института Шейн Фредерик разрабатывает новую статью для проверки интеллекта:
[gview file = ”http://mitsloan.mit.edu/alumni/pdf/Winter08-InnovationAtWork.pdf »]Итак, если вы ответили 10 центов как цену мяча, вы полагаетесь на свой первый импульс, системный, как на свое руководство. Но если вы ответили правильно, то это было бы рефлексивное объективное мышление, система два.
Я признаю, что сначала я ответил 10 центов, но когда мне сказали, что это неправильно, я потратил некоторое время и решил это.
Итак, мяч стоит 5 центов . Вы понимаете почему?
Бита была на долларов больше, чем мяч на .