Закон куга – Форд Куга. Один из лучших представителей среднеразмерных SUV 2018-2019 ПДД, КоАП, ГИБДД онлайн
Закон Гука | Все формулы
Закон Гука — Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L), записав коэффициент упругости как
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
В формуле мы использовали :
— Сила натяжения стержня
— Коэффициент упругости (Коэффициент деформации)
— Абсолютное удлинение стержня
— Модуль Юнга
— Площадь поперечного сечения
— Длина стержня
Сила упругости. Закон Гука | ЭТО ФИЗИКА
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
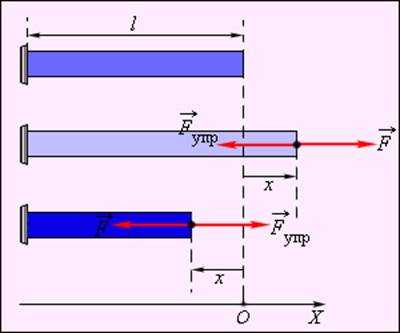
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
|
Рисунок 1.12.1. Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука.
Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м).
Коэффициент жесткости зависит от материала, формы и размеров тела. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме.
Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется
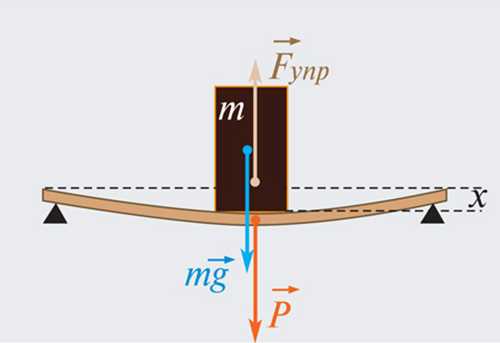
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
|
Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:
Сила с которой тело действует на стол, называется весом тела.
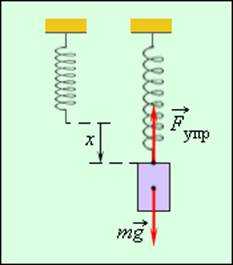
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
|
Рисунок 1.12.3. Деформация растяжения пружины. |
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

www.its-physics.org
Закон Гука — это… Что такое Закон Гука?
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke)[1]. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как
Величина называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Обобщённый закон Гука
В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
где — тензор напряжений, — тензор деформаций. Для изотропного материала тензор содержит только два независимых коэффициента.
Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.
См. также
Примечания
Ссылки
dic.academic.ru
Закон Гука для сопромата.
Сопротивление материалов
Закон Гука для продольных нагрузок
Более 350 лет назад 25-летний английский физик Роберт Гук (в англоязычной транскрипции — Хук) сформулировал зависимость между относительным линейным удлинением тела и величиной растягивающей тело силы.
В оригинале формулировка закона, предложенная Гуком, звучит примерно так:
«Какова сила, таково и удлинение».
В современной трактовке эта зависимость в общем виде формулируется следующим образом:
Казалось бы, очевидный вывод, который напрашивается естественным образом – чем больше сила, приложенная к брусу, тем в большей степени он деформируется. Тем не менее, заслуга Гука заключается в том, что именно он обратил внимание, на линейную (прямо пропорциональную) зависимость между нагрузкой и относительной деформацией.
Открытия многих, казалось бы — очевидных, закономерностей совершают гении. Ведь в течении предшествующих Ньютону человеческих поколений считалось, что чем легче тело, тем дольше оно падает на земную поверхность с высоты. И лишь гений смог опровергнуть это заблуждение миллионов людей. По сути, только великий Эйнштейн сделал неочевидное открытие, которому, впрочем, предшествовали научные исследования и гипотезы многих талантов.
Долгое время закон Гука являлся единственным инструментом новоявленной науки сопротивление материалов, и лежал в основе всех расчетов конструкций на прочность и жесткость. Лишь спустя много лет учеными были установлены более сложные (непропорциональные) зависимости между напряжениями и приложенными к элементам конструкции силовыми факторами, которые, впрочем, тоже основываются на законе Гука.
Роберт Гук (1635—1703) считается одним из талантливейших ученых своего времени. Обладавший кипучей творческой энергией, он совершил много интересных открытий в самых разных науках – фундаментальной физике, термодинамике, акустике, оптике, биологии. Достаточно сказать, что Гуку многие ученые отдают пальму первенства в открытии закона всемирного тяготения, считая, что он раньше Ньютона пришел к его осознанию.
Тем не менее, этот человек останется в памяти потомков, как автор знаменитого закона Гука.
Математически закон Гука для деформаций растяжения и сжатия можно записать так:
σ = Еε,
где:
σ – напряжение в сечении бруса,
ε — относительное удлинение бруса, которое определяется по формуле ε = Δl/l (здесь Δl – абсолютное удлинение бруса, l – начальная длина бруса),
Е – коэффициент пропорциональности, который называют модулем продольной упругости (или модулем упругости первого рода, или модулем Юнга).
Коэффициент Е является справочной (определяемой экспериментально) величиной, характеризующей способность материала противостоять деформации и измеряется в Паскалях (1 Па = Н/м2).
Поскольку 1 Паскаль – очень маленькая величина (муха весом 14 мг, севшая на столик площадью 1 м2 окажет на него давление, примерно равное 0,00014 Па), поэтому чаще применяют ее производную – 1 МПа (миллион Паскалей, или 1 МПа = 1 000 000 Па).
Математическое выражение закона Гука можно представить в расширенном виде, подставив вместо σ (напряжения) его зависимость от силы и площади сечения:
σ = F/A, и вместо ε (удельное удлинение) выражение Δl/l. Тогда получим:
F/A = Е(Δl/l), откуда можно выразить абсолютное удлинение (укорочение) бруса в результате приложения внешней силы F:
Δl = Fl/(EA).
Это выражение можно сформулировать следующим образом: абсолютное удлинение (укорочение) бруса прямо пропорционально приложенной внешней нагрузке и длине бруса и обратно пропорционально площади поперечного сечения бруса.
Выражение ЕА, стоящее в знаменателе дроби, часто называют жесткостью сечения при растяжении и сжатии.
Приведенные формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из однородного материала и при постоянной продольной силе. Если брус имеет ступенчатую форму, или состоит из участков, изготовленных из разных материалов, и нагружен на разных участках несколькими продольными силами, то абсолютное изменение длины всего бруса определяют, как сумму абсолютных удлинений его отдельных участков:
Δl = Σ (Δli)
В заключение следует отметить, что закон Гука справедлив в ограниченном диапазоне внешних нагрузок и не применим, когда некоторые напряжения (или деформации) достигают предельных значений, характерных для каждого материала. При превышении предельных значений напряжений линейная зависимость между нагрузками и деформациями не наблюдается.
***
Материалы раздела «Сопротивление материалов»:
Метод сечений. Напряжения
№ вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Правильный вариант ответа |
1 |
2 |
1 |
2 |
3 |
2 |
1 |
3 |
1 |
3 |
k-a-t.ru
Обобщенный закон Гука
Законом Гука обычно называют линейные соотношения между компонентами деформаций и компонентами напряжений.
Возьмем элементарный прямоугольный параллелепипед с гранями, параллельными координатным осям, нагруженный нормальным напряжением σх, равномерно распределенным по двум противоположным граням (рис. 1). При этом σy = σz = τхy = τхz = τyz = 0.
Рис. 1
Вплоть до достижения предела пропорциональности относительное удлинение дается формулой
где Е — модуль упругости при растяжении. Для стали Е = 2*105МПа, поэтому деформации очень малы и измеряются в процентах или в 1*105 (в тензометрических приборах, измеряющих деформации).
Удлинение элемента в направлении оси х сопровождается его сужением в поперечном направлении, определяемом компонентами деформаций
где μ – константа, называемая коэффициентом поперечного сжатия или коэффициентом Пуассона. Для стали μ обычно принимается равным 0,25–0,3.
Если рассматриваемый элемент нагружен одновременно нормальными напряжениями σx, σy, σz, равномерно распределенными по его граням, то добавляются деформации
Производя наложение компонент деформации, вызванных каждым из трех напряжений, получим соотношения
Эти соотношения подтверждаются многочисленными экспериментами. Примененный метод наложения или суперпозиции для отыскания полных деформаций и напряжений, вызванных несколькими силами, является законным, пока деформации и напряжения малы и линейно зависят от приложенных сил. В таких случаях мы пренебрегаем малыми изменениями размеров деформируемого тела и малыми перемещениями точек приложения внешних сил и основываем наши вычисления на начальных размерах и начальной форме тела.
Рис. 2
Следует отметить, что из малости перемещений еще не следует линейность соотношений между силами и деформациями. Так, например, в сжатом силами Q стержне, нагруженном дополнительно поперечной силой Р, даже при малом прогибе δ возникает дополнительный момент М = Qδ, который делает задачу нелинейной. В таких случаях полные прогибы не являются линейными функциями усилий и не могут быть получены с помощью простого наложения (суперпозиции).
Экспериментально установлено, что если касательные напряжения действуют по всем граням элемента, то искажение соответствующего угла зависит только от соответствующих компонентов касательного напряжения.
Константа G называется модулем упругости при сдвиге или модулем сдвига.
Общий случай деформации элемента от действия на него трех нормальных и трех касательных компонентов напряжений можно получить с помощью наложения: на три линейные деформации, определяемые выражениями (5.2а), накладываются три деформации сдвига, определяемые соотношениями (5.2б). Уравнения (5.2а) и (5.2б) определяют связь между компонентами деформаций и напряжений и называются обобщенным законом Гука. Покажем теперь, что модуль сдвига G выражается через модуль упругости при растяжении Е и коэффициент Пуассона μ. Для этого рассмотрим частный случай, когда σх = σ, σy = –σ и σz = 0.
Вырежем элемент abcd плоскостями, параллельными оси z и наклоненными под углом 45° к осям х и у (рис. 3). Как следует из условий равновесия элемента 0bс, нормальные напряжения σv на всех гранях элемента abcd равны нулю, а касательные напряжения равны
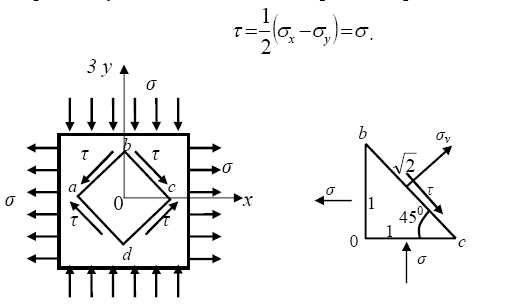
Рис. 3
Такое напряженное состояние называется чистым сдвигом. Из уравнений (5.2а) следует, что
то есть удлинение горизонтального элемента 0c равно укорочению вертикального элемента 0b: εy = –εx.
Угол между гранями аb и bc изменяется, и соответствующую величину деформации сдвига γ можно найти из треугольника 0bс:
Отсюда следует, что
и при малых γ получим
Отсюда и, следовательно,
Уравнения (5.2а) и (5.2б) определяют компоненты деформаций через компоненты напряжений. Выведем обратные соотношения — напряжения через деформации.
Складывая уравнения (5.2а) и используя обозначения
получаем зависимость между средней деформацией и средним напряжением
Поскольку Зε0 равно объемному расширению, величину называют модулем объемного расширения. Используя соотношения (5.4) и решая уравнения (5.2а) относительно σх, σу, σz, получим
Если учесть, что , то закон Гука запишется в виде
Тогда соотношения (4.11) можно записать в виде
Если ввести символ Кронекера , то закон Гука в краткой записи примет вид
vse-lekcii.ru
закон Гука
Министерство образования АР Крым
Таврический Национальный Университет им. Вернадского
Исследование физического закона
ЗАКОН ГУКА
Выполнил: студент 1 курса
физического факультета гр. Ф-111
Потапов Евгений
Симферополь-2010
План:
Связь между какими явлениями или величинами выражает закон.
Формулировка закона
Математическое выражение закона.
Каким образом был открыт закон: на основе опытных данных или теоретически.
Опытные факты на основе которого был сформулирован закон.
Опыты, подтверждающие справедливость закона, сформулированного на основе теории.
Примеры использования закона и учета действия закона на практике.
Литература.
Связь между какими явлениями или величинами выражает закон:
Закон Гука связывает такие явления, как напряжение и деформацию твердого тела, модуль силы упругости и удлинение. Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению. Удлинением называется характеристика деформативности материала, оцениваемая по увеличению длины образца из этого материала при растяжении. Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации. Напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Деформа́ция — изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга. Эти понятия связаны так называемым коэффициентом жесткости. Он зависит от упругих свойств материала и размеров тела.
Формулировка закона:
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.
Формулировка закона — сила упругости прямо пропорциональна деформации.
Математическое выражение закона:
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.
Если ввести относительное удлинение
инормальное напряжение в поперечном сечении
то закон Гука запишется так
В такой форме он справедлив для любых малых объёмов вещества.
В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга Cijkl и содержит 81 коэффициент. Вследствие симметрии тензора Cijkl, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
где σij — тензор напряжений, —тензор деформаций. Для изотропного материала тензор Cijkl содержит только два независимых коэффициента.
Каким образом был открыт закон: на основе опытных данных или теоретически:
Закон был открыт в 1660 году английским учёным Робертом Гуком (Хуком) на основе наблюдений и экспериментов. Открытие, как утверждал Гук в своём сочинении «De potentia restitutiva», опубликованном в 1678, сделано им за 18 лет до этого времени, а в 1676 было помещено в другой его книге под видом анаграммы «ceiiinosssttuv», означающей «Ut tensio sic vis». По объяснению автора, вышесказанный закон пропорциональности применяется не только к металлам, но и к дереву, камням, рогу, костям, стеклу, шёлку, волосу и проч.
Опытные факты на основе которых был сформулирован закон:
История об этом умалчивает..
Опыты, подтверждающие справедливость закона, сформулированного на основе теории:
Закон сформулирован на основе опытных данных. Действительно, при растягивании тела (проволоки) с определенным коэффициентом жесткости k на расстояние Δl, то их произведение будет равно по модулю силе, растягивающей тело (проволоку). Такое соотношение будет выполняться, однако, не для всех деформаций, а для небольших. При больших деформациях закон Гука перестает действовать, тело разрушается.
Примеры использования закона и учета действия закона на практике:
Как следует из закона Гука, по удлинению пружины можно судить о силе, действующей на нее. Этот факт используется для измерения сил с помощью динамометра – пружины с линейной шкалой, проградуированной на разные значения сил.
Литература.
1. Интернет-ресурсы: — сайт Википедия (http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%93%D1%83%D0%BA%D0%B0).
2. учебник по физике Перышкин А.В. 9 класс
3. учебник по физике В.А. Касьянов 10 класс
4. лекции по механике Рябушкин Д.С.
6
studfiles.net
первая неисправность и первое ТО — журнал За рулем
Подводим итоги летней эксплуатации и планового технического обслуживания.
 Ford Kuga из парка ЗР
Ford Kuga из парка ЗРFord Kuga из парка ЗР
Напомню, что кроссовер Форд Куга попал на длительный тест в редакцию ЗР в начале года. Если точнее, то в апреле, когда дневная температура колебалась возле отметки в 10°С, а ночью опускалась ниже нуля. Многие в таких условиях задаются вопросом — греть или не греть машину перед началом поездки? Я не грел или почти не грел. Старался лишь не усердствовать с педалью акселератора первые километры пути. Отчасти поэтому Куга несколько расстраивала завышенными показателями среднего расхода топлива. К примеру, бортовой компьютер высвечивал порой неприличные 14,5 л на сотню. Фактический же расход был чуть меньше. С приходом лета аппетит стал умеренным: 12,5 л при езде по городу. На трассе 150-сильный турбодвигатель Куги съедал не больше 10 л на 100 км.
 Серьезных претензий к эргономике рабочего места водителя нет. Повсюду достаточно мягкий пластик, на руле приятная на ощупь кожаная обивка. Центральный подлокотник для пущего удобства можно сдвинуть вперед. Словом, за рулем Куги вполне себе комфортно и удобно, даже в дальней поездке.
Серьезных претензий к эргономике рабочего места водителя нет. Повсюду достаточно мягкий пластик, на руле приятная на ощупь кожаная обивка. Центральный подлокотник для пущего удобства можно сдвинуть вперед. Словом, за рулем Куги вполне себе комфортно и удобно, даже в дальней поездке.Серьезных претензий к эргономике рабочего места водителя нет. Повсюду достаточно мягкий пластик, на руле приятная на ощупь кожаная обивка. Центральный подлокотник для пущего удобства можно сдвинуть вперед. Словом, за рулем Куги вполне себе комфортно и удобно, даже в дальней поездке.
Дело привычки
Материалы по теме
www.zr.ru