Чем эллипс отличается от овала – Никогда не задумывался чем отличается овал от эллипса, хотя когда-то…

Чем отличается овал от эллипса?

У В. И. Даля: правильный овал — это эллипс.
Эллипс — математическое выражение овала. Каждый эллипс можно точно описать с помощью всего лишь нескольких характе­ристик (рисунок 1.7).

S,S2 на рисунке 1.7 — длина большой оси эллипса. S3S4 — дли­на малой оси эллипса. Эллипс теперь определяется уравнением

Для нас представляет интерес (в контексте анализа Фибонач­чи) отношение главной и малой оси эллипса, выраженное на ма­тематическом языке в следующей формуле

Рисунок 1.7 Геометрия ФИ-эллипса. Источник: FAM Research, 2000.

Эллипс превращается в ФИ-эллипс во всех тех случаях, где от­ношение большой оси к малой оси эллипса является элементным числом ряда ФИ 0,618-1,000-1,618-2,618-4,236-6,854- и так далее. Круг — специальный тип ФИ-эллипса, в котором а = Ь и от­ношение а-=-Ь= 1.

ФИ-эллипсы предпочтительнее всех других возможных эллип­сов (с отношениями главных осей, деленных на малые оси, ины­ми, чем числа ряда ФИ) , поскольку эмпирические исследования показали, что люди находят приближения ФИ-эллипсов визуаль­но значительно более удовлетворительными.

Когда участники исследовательского проекта сталкивались с различными формами эллипсов и их спрашивали об уровне ком­форта, пробное эмпирическое исследование дало результаты, по­казанные в Таблице 1.1.

Три наблюдателя из четырех предпочли эллипсы, имеющие оси, чьи отношения равны отношению ФИ-эллипса (1,618) или так близко приближены к ФИ-эллипсу, чтобы были почти от не­го неотличимы.

ФИ — Фибоначчи

Для того чтобы нарисовать овал, выберите на панели инструментов рисования инструмент Oval (Овал) .

Отсмеявшись и утерев слёзы, мы просмотрели остальные ответы и поняли, что интернет предлагает решения на все случаи жизни, нужно только определить, какой именно у вас случай. Мы попытались классифицировать предлагаемые ответы, чтобы легче было выбирать. Итак,

Для тех, кто не умеет рисовать
Для того чтобы нарисовать овал Вам нужно нажать кнопку мыши (левую / среднюю / правую) , перетащить указатель мыши на другое место и отпустить.

Для тех, кто не знает, с чего начать
Нарисуй овал (круг) , поставь точку в середине круга (сверху, снизу, справа, слева)

Для менеджеров
Если Вы попробуете нарисовать овал или прямоугольник без выбора цветов заливки и линии одновременно, то вы ничего не нарисуете.

Для любителей нестандартных решений
Инструментом Эллипс нарисовать овалы.

Для развития абстрактного мышления
Нарисуем треугольник и овал почти в форме яйца.
Если нарисовать овал, затем соединить его с вершиной треугольника, то получим объемную форму конус, он похож на перевернутый стаканчик для мороженого.

Для тупых
Удалите старый овал и нарисуйте овал снова выбранными цветами.

Для ленивых
Перейдите в рабочую область и нарисуйте овал.

Для грустных
В центре листа нарисуйте овал, в котором напишите «поем песни»

Для юннатов (юных натуралистов, если кто не в курсе)
В отдельных слоях нарисовать три овала: голову, туловище и животик (каждый в отдельном слое) .
В отдельном слое нарисовать овал, наклонить его по горизонтали на 45°, дорисовать «Карандашом» лапку.

Рисуйте на здоровье!

otvet.mail.ru

Чем отличается овал от эллипса |

Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.

Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.

Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.

Эллипс к содержанию ↑

Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.

Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.

1. Объём. Овал – более широкое понятие, в объём которого входит эллипс.
2. Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.

charmsoflife.ru

Чем отличается овал от эллипса — Что и Как

Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.

Что такое овал и эллипс

Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.

Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
Эллипс

Разница между овалом и эллипсом

Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.

TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:

Объём. Овал – более широкое понятие, в объём которого входит эллипс.
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.

allways.ru

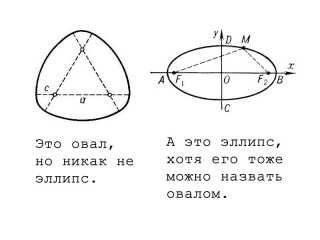
Никогда не задумывался чем отличается овал от эллипса, хотя когда-то…

Никогда не задумывался чем отличается овал от эллипса, хотя когда-то учил геометрию, причем знал ее весьма неплохо. 😉
Эллипс, [греч. elleipsis — опущение, пропуск].геом. замкнутая кривая линия, получаемая от пересечения конуса плоскостью, непараллельной основанию; внутри Э. находятся две точки (фокусы), сумма расстояний которых от каждой точки кривой (радиусы=векторы) есть величина постоянная, равная большей оси (большому диаметру) Э. Диаметр, перпендикулярный к большой оси и делящий ее на две равные части, наз. малой осью Э. Отношение расстояния между фокусами к большой оси назыв. эксцентриситетом. Орбиты планет суть Э. Овалы (франц., единственное число ovale, от лат. ovum — яйцо), замкнутые выпуклые плоские кривые. При этом под выпуклостью понимают свойство кривой иметь с любой прямой не более двух (действительных) общих точек. Примером О. может служить эллипс (в частности, окружность). Если О. имеет в каждой своей точке определённую касательную, то любому направлению на плоскости соответствуют две и только две касательные, параллельные этому направлению. Известно много теорем о свойствах О.; в качестве примера можно привести следующие. 1) На каждом О. имеется не менее четырёх точек, в которых кривизна его достигает максимума или минимума (теорема о четырёх вершинах; в случае эллипса таких точек ровно четыре — концы большой и малой осей). 2) Если расстояние d между любыми двумя параллельными касательными к О. одно и то же для всех направлений (О. постоянной ширины), то длина О. равна p

d. Простейшим О. постоянной ширины является окружность; др. примером может служить фигура (рис.), получаемая следующим образом: из вершин равностороннего треугольника со стороной а проводят шесть дуг окружностей, радиус трёх из них — произвольный отрезок с, радиус трёх других — отрезок, равный а + с.
Это по-научному. 😉
Получается, что любой эллипс — это овал, но не всякий овал — эллипс.

Tags: геометрия, овал, эллипс

newby-diz.livejournal.com

Чем отличается овал от эллипса

Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.

Что такое овал и эллипс

Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
Эллипс

Разница между овалом и эллипсом

Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.

Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.

TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:

Объём. Овал – более широкое понятие, в объём которого входит эллипс.
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.

vyeiske.ru

Овалы и эллипсы — блог Привычка не думать

Добрый день.

А давайте попробуем написать краткие сочинения для нынешних выпускников на тему «Почему стоит выбрать изучение такой-то науки?» Вдруг кто-то сейчас как раз колышется с выбором, в какой вуз или на какой факультет податься, а мы ему ещё сильнее карты спутаем… Ниже предлагаю свою версию про всякую математику и геометрию (ранее была и другая запись на близкую тему — «Зачем изучать математику?») Приглашаю вас поделиться своим вариантом!

Итак, долгое время я считал, что «овал» — это жаргонное название эллипса. Потом начались уроки черчения, на которых нас учили рисовать в том числе и овалы (как четвёрку дуг: две одного радиуса и две — другого). Уже тогда было понятно, что эллипс циркулем и линейкой не нарисовать, поэтому по данному свойству овал казался куда удобнее, хоть и нелепее. А затем и вовсе началась эпоха интернета, поэтому узнать о том, что такое овал может каждый, но уже не каждому это понравится или даже захочется сделать.

Чем же хорошо нам всем знакомый эллипс драматически отличается от множества других хорошо знакомых фигур? Оказывается, мы не можем выразить длину дуги произвольного эллипса в элементарных функциях. Вот для частных случаев ещё справиться можем: например, если эллипс является окружностью, то всё хорошо — длина дуги выражается как удвоенное произведения радиуса и числа Пи. А вот с произвольным эллипсом, задаваемым парой радиусов a и b, такое уже не пройдёт.

Кстати, легко понять, что для частного случая овала с уроков черчения никаких проблем нет: раз он состоит из дуг окружностей, то про него мы всё знаем.

Но всё равно сложно избавиться от ощущения, что что-то здесь не так. Как может простой эллипс, легко получаемый растяжением окружности, вызывать какие-то проблемы, если с самой окружностью всё достаточно легко? Чтобы понять это, давайте сравним периметры и площади у следующих фигур:

Казалось бы, если мы знаем площадь круга радиуса a, то знаем и площадь эллипса эллипса с радиусами

a и b (достаточно домножить площадь круга на b/a, чтобы получить искомое значение). Этот же трюк прекрасно работает на квадратах, что совершенно правильно и естественно. В чём же проблема с периметром? Может показаться, что всё должно быть совершенно аналогично. Но мысленный эксперимент с растяжением квадрата эту теорию легко ломает… Иногда полезно попредставлять такие штуки, чтобы лучше чувствовать, чем отличается длина от площади.

К сожалению, описанную выше проблему с невозможностью выразить длину дуги эллипса нередко формулируют неверно (что-то вроде «на дворе 21 век, а математики так и не смогли найти формулу эллипса» или даже грубее; иногда, видимо, желая упростить, журналисты позволяют себе говорить, что число Пи равно трём, поэтому фраза про математиков, которые «до сих пор не могут одолеть эллипс» не слишком раздражает). Как вы понимаете, эллипс человечество знает очень давно и исследовало весьма плотно. Дело не в том, что математики чего-то не смогли, а в том, что это принципиально невозможно.

Казалось бы, обычная сплющенная окружность, а уже вылезают дивные эффекты! Если вас завораживает эта мысль и вы как раз заканчиваете школу, то хорошо подумать о поступлении на математический факультет определённо стоит. Ведь гораздо интереснее учиться тому, что вам нравится (см. об этом ещё тут).

А если вы любите всякое красивое и геометрическое, то рекомендую статью с массой внятных анимированных картинок про арбелос.

my-tribune.blogspot.com