Ученый перельман – Григорий Перельман – биография, фото, личная жизнь, гипотеза Пуанкаре 2019
Григорий Перельман – биография, фото, личная жизнь, гипотеза Пуанкаре 2019
Биография
Гениальный математик Григорий Перельман потряс научный мир, доказав гипотезу Пуанкаре – одну из сложнейших загадок тысячелетия. А обывателей удивил отказ небогатого ученого от положенной премии в размере миллиона долларов. Постепенно сам гений и его затворнический образ жизни стали загадкой, сравнимой по сложности с доказанной теоремой.
Детство и юность
Григорий Яковлевич ведет скрытный образ жизни. Факты детства, юности и личной жизни ученого известны со слов соседей, школьных учителей и одноклассников, коллег, работавших вместе с математиком.
 Математик Григорий Перельман
Математик Григорий ПерельманПерельман родился 13 июня 1966 года в Ленинграде. Фамилия гениального математика говорит сама за себя о национальности. Еврейский мальчик с детства проявлял неимоверные способности и интерес к учебе. В то время, когда сверстники гоняли мяч во дворе, маленький Гриша предпочитал читать книги и играть в шахматы.
Вопреки расхожему мнению Яков Исидорович Перельман, знаменитый ученый, автор книг и популяризатор наук, не является родственником Григория Яковлевича.
 Григорий Перельман в детстве
Григорий Перельман в детствеОтец Григория — инженер-электрик. В 1993 году Перельман-старший иммигрировал на историческую родину в Израиль, как и тысячи его соотечественников в 90-х. Мать будущего выдающегося математика осталась с детьми в Ленинграде, преподавала математику в училище.
У Григория Яковлевича есть младшая сестра, построившая научную карьеру. Получив диплом математика в Санкт-Петербургском университете, женщина позже уехала в Швецию. С 2007 года работает программистом в Стокгольме.
 Григорий Перельман без бороды
Григорий Перельман без бородыК тому времени, когда мальчик пошел в школу, он значительно превосходил одноклассников в знаниях, с легкостью считал в уме трехзначные числа. Учителя Перельмана вспоминают, что школьник вел беседы на равных со взрослыми.
Магия логики и чисел привлекала Григория Яковлевича. С 5 класса мальчик посещал математический центр во Дворце пионеров. Наставником юных вундеркиндов был доцент Педагогического университета имени А. И. Герцена Сергей Рукшин. Юный Гриша получал награды за участие в олимпиадах, в том числе заслужил высший балл на международной математической олимпиаде.
 Григорий Перельман в молодости
Григорий Перельман в молодостиОкончив девятилетку в обычной ленинградской школе, выпускник перешел в специализированную физико-математическую школу № 239. Без сомнения, трудолюбивый и талантливый Перельман учился идеально. Подвела физическая подготовка. Провал по сдаче норм ГТО помешал получить выпускнику золотую медаль.
Неудивительно, что после школьной скамьи Григория без вступительных экзаменов приняли в Ленинградский государственный университет на факультет математики и механики. В вузе Перельман продолжил блистать на олимпиадах, за превосходные результаты обучения получал Ленинскую премию.
Наука
После выпуска последовала аспирантура, затем защита докторской. В результате одаренный ученый остался работать при ставшем родным университете в должности старшего научного сотрудника.
 Григорий Перельман
Григорий ПерельманВ начале 90-х годов талантливый ученый отправился в США, где в рамках обмена опытом посетил несколько университетов. В Соединенных Штатах математик читал лекции, встречался с коллегами. Вскоре аскетичному Перельману наскучила Америка, и ученый вернулся на родину.
Возобновив работу в ленинградском вузе, математик начинает упорно трудиться над загадкой тысячелетия, которую не в силах были разгадать гениальные ученые столетия. Стоит отметить, что за несколько лет до этого началось увлечение Перельмана топологией. Ранее математик сумел доказать гипотезу о душе, что предшествовало изучению гипотезы Пуанкаре.
 Григорий Перельман доказывает гипотезу Пуанкаре
Григорий Перельман доказывает гипотезу ПуанкареСмысл доказательства гипотезы, впрочем, как и саму суть, невозможно описать простым языком, понятным для далекого от высшей математики человека. Открытия, сделанные математиком, имеют огромное значение в изучении Вселенной, в работе с нанотехнологиями.
Кроме того, гипотеза утверждает, что особенность формы Вселенной приводит к тому, что ее можно стянуть в одну точку. Это, в свою очередь, косвенно подтверждает теорию Большого взрыва. Сторонники теологического происхождения Вселенной получили повод для сомнений о Боге как о создателе всего сущего. Гипотеза Пуанкаре доказывает, что Бога нет.
 Григорий Перельман возле своего подъезда
Григорий Перельман возле своего подъездаВ 2002-2003 годах Перельман публикует статьи, раскрывающие суть доказательства. Три независимые группы математиков, проверив доводы, подтвердили полное доказательство.
В 2003 году Перельман посетил США, читал лекции о собственном открытии, делился опытом и с соотечественниками. А в 2005 ученый неожиданно уходит с кафедры и запирается в квартире в Купчино, где живет с больной мамой.
Личная жизнь
Затворнический образ жизни оставляет сотни вопросов. Главный, интересующий журналистов и граждан, — это причина, по которой Григорий Перельман отказался от по праву принадлежащих ему денег. Речь идет о премии института Клэя. Математический институт составил список семи загадок, за решение которых полагается награда в миллион долларов. Гипотеза Пуанкаре входила в данный список.
 Григорий Перельман и его мама
Григорий Перельман и его мамаРазумеется, узнав об открытии российского ученого, учредители незамедлительно обратились к ученому. Каково же было всеобщее удивление, когда математик отказался от миллиона долларов без объяснения причин.
Вскоре Григорий Яковлевич вовсе перестал общаться с прессой. Российских журналистов попросту игнорирует, а зарубежным отказывает в интервью. Новости о подобном поведении ученого повлекли за собой слухи о болезни Перельмана. Утверждали, что гений страдает аутизмом. Впрочем, достоверных подтверждений или заключений врачей до сих пор не обнародовано.
Григорий Перельман сейчас
Известно, что ученый живет с мамой, которая тяжело болеет. Жены у математика нет. По рассказам учительницы Григория Яковлевича, которая поддерживает с ним отношения, живут мать с сыном бедно.
 Григорий Перельман сейчас
Григорий Перельман сейчасВ 2018 году появились сведения о том, что математик перебрался в Швецию. Однако источники в лице соседей и продавцов магазинов опровергли слухи и подтвердили, что Перельман никуда не уезжал.
Интересные факты
- Во время работы в Штатах ученый удивлял зарубежных коллег непритязательностью и отрешенностью от бытовых потребностей. Любимой едой математика стали бутерброды с сыром, которые Григорий Яковлевич запивал кефиром или молоком. Рестораны и изобилие продуктовых магазинов не интересовали «странного русского».
 Григорий Перельман
Григорий Перельман- В детстве Григорий увлекался музыкой. Мать привила сыну обожание классических композиторов. Она же, будучи талантливой скрипачкой, познакомила Гришу с инструментом. Перельман с удовольствием посещал музыкальную школу, а потом перед ним встал непростой выбор — поступить в консерваторию или же посвятить себя точным наукам.
- В Сети появлялись высказывания сторонников теории заговора о том, что Перельман — самый влиятельный человек на земле, поскольку знает, как управлять Вселенной. Разумеется, что такая личность не избежала внимания секретных служб, и общение с окружающими запрещено для ученого.
Цитаты
Я знаю, как управлять Вселенной. И скажите – зачем же мне бежать за миллионом?
Весь мир пронизывает пустота, а она подчиняется формулам — это даёт нам безграничные возможности.
Если можно тренировать руки и ноги, то почему нельзя тренировать мозг?
Неразрешимой задачи, пожалуй, нет. Трудно решаемой. Так точнее.
Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху? Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться.
Награды и премии
- 1991 — премия «Молодому математику» Санкт-Петербургского математического общества
- 1996 — Премия Европейского математического общества для молодых математиков
- 2006 — премия «Медаль Филдса»
- 2010 — премия Математического института Клэя
24smi.org
Российский математик Перельман отказался от высшей награды — Российская газета
Вчера завершилась интрига вокруг награждения медалями Филдса — математическим аналогом Нобелевской премии. Среди четырех лауреатов двое россиян: работающий сейчас в США Андрей Окуньков и названный на Западе русским гением питерский ученый Григорий Перельман.
Награды лауреатам вручал король Испании Хуан Карлос I. Как и прогнозировалось, Григорий Перельман на церемонии не появился. Он никак не отреагировал на сообщение о награде и приглашение ее получить.
Четыре года назад Перельман поразил математический мир, решив одну из семи «задач тысячелетия» — гипотезу Пуанкаре, сформулированную им еще в начале XX века.
За доказательство каждой из задач «великолепной семерки» Математический институт им. Клэя (США) присудил приз в миллион долларов. Но и эту награду россиянин, судя по всему, получать не собирается.
Понять причину отказа от всяческих наград широкой публике так же сложно, как и составить какое-то представление о доказанной ученым гипотезе. Она касается геометрии многомерных пространств и является ключом в сферу топологии.
— Это центральная проблема математики и физики, попытка понять, какой формы может быть Вселенная, — сказал известный математик Маркус Дю Сотой из Оксфорда. — К ней очень трудно подобраться, но российский математик добился успеха.
Ученые по-разному комментируют отказ Перельмана получать престижную награду. Так, историк математики из Оксфорда Джереми Грей сказал: «Я не представляю себе его в длинном лимузине с четырьмя роскошными женщинами, размахивающим чеком в воздухе. Это не в его стиле». А математик Артур Яффе из Гарварда заявил: «Думаю, что он очень нетривиальный человек, который не хочет, чтобы его вовлекали в пышные церемонии и идолопоклонство. Но он доводит это до крайности, что можно счесть легким безумием».
Необычным был и способ, который Перельман избрал для обнародования своего доказательства. Вместо того чтобы опубликовать его в солидном научном журнале, что, кстати, было обязательным условием для присуждения приза в миллион долларов, Перельман разместил свою работу на одном из архивов Интернета. Хотя доказательство заняло всего 61 страницу, оно произвело сенсацию в научном мире. Математики с нетерпением ожидали более развернутое решение, ведь талантливый россиянин лишь обозначил реперные точки на пути к нему. Но время шло, а Перельман молчал, несмотря на все просьбы самых авторитетных научных журналов откликнуться. Зато другие не дремали. Китайские и американские математики фактически сделали работу за него. Последнее подробное решение занимает 473 страницы!
Григорий Перельман родился в 1966 году в Ленинграде. Окончил физико-математическую школу N 239, побеждал на многих олимпиадах. Одноклассники вспоминают, что на уроках он сидел на последней парте и оттуда порой объяснял преподавателям, что та или иная математическая задача имеет более экономное и изящное решение, нежели предложенное в учебнике. После окончания школы он без экзаменов был зачислен на механико-математический факультет Ленинградского университета. Работал в Санкт-Петербургском математическом институте им. Стеклова. В конце 80-х годов перебрался в США, где читал лекции в нескольких университетах, затем вернулся в свой институт.
С 1 января этого года Григорий Перельман уволился из института. Куда ушел? Этого никто из бывших коллег не знает. По словам же знакомых, гений «ушел в леса» по грибы под Санкт-Петербургом.
rg.ru
Перельман, Григорий Яковлевич — это… Что такое Перельман, Григорий Яковлевич?
В Википедии есть статьи о других людях с такой фамилией, см. Перельман. Григо́рий Я́ковлевич Перельма́н (р. 13 июня 1966, Ленинград, СССР) — выдающийся российский математик, первым доказавший гипотезу Пуанкаре.[1][2]Биография
Григорий Перельман родился 13 июня 1966 года в Ленинграде в еврейской семье. Его отец Яков был инженером-электриком, в 1993 году эмигрировал в Израиль. Мать, Любовь Лейбовна, осталась в Санкт-Петербурге, работала учителем математики в ПТУ[3][нет в источнике 362 дня]. Именно мать, игравшая на скрипке, привила будущему математику любовь к классической музыке.
До 9 класса Перельман учился в средней школе на окраине города, однако, в 5 классе начал заниматься в математическом центре при Дворце пионеров под руководством доцента РГПУ Сергея Рукшина, чьи ученики завоевали множество наград на математических олимпиадах. В 1982 году в составе команды советских школьников завоевал золотую медаль на Международной математической олимпиаде в Будапеште, получив полный балл за безукоризненное решение всех задач
Был без экзаменов зачислен на математико-механический факультет Ленинградского государственного университета. Побеждал на факультетских, городских и всесоюзных студенческих математических олимпиадах. Все годы учился только на «отлично». За успехи в учёбе получал Ленинскую стипендию. Окончив с отличием университет, поступил в аспирантуру (руководитель — академик А. Д. Александров) при Ленинградском отделении Математического института им. В. А. Стеклова (ЛОМИ — до 1992 г.; затем — ПОМИ). Защитив в 1990 году кандидатскую диссертацию, остался работать в институте старшим научным сотрудником.
В начале 1990-х годов Перельман приехал в США, где работал научным сотрудником в разных университетах. Удивлял коллег аскетичностью быта, любимой едой были молоко, хлеб и сыр. В 1996 году вернулся [5] в Санкт-Петербург, продолжает работать в ПОМИ, где он в одиночку трудится над решением Проблемы Пуанкаре.
В 2002 — 2003 годах Григорий Перельман публикует в Интернете свои три знаменитых статьи, в которых он кратко изложил свой оригинальный метод решения Проблемы Пуанкаре:
- The entropy formula for the Ricci flow and its geometric applications[6]
- Ricci flow with surgery on three-manifolds[7]
- Finite extinction time for the solutions to the Ricci flow on certain three-manifolds[8]
В 2003 году Григорий Перельман принял приглашение посетить ряд американских университетов, где он сделал серию докладов о своей работе по доказательству Проблемы Пуанкаре[9]. В Америке Перельман потратил много времени объясняя свои идеи и методы как в организованных для него публичных лекциях, так и во время личных встреч с рядом математиков. После своего возвращения в Россию, он отвечал на многочисленные вопросы своих зарубежных коллег по электронной почте.
В 2004 — 2006 годах верификацией результатов Перельмана занимались три независимые группы математиков: 1) Bruce Kleiner, John Lott, Мичиганский университет; 2) Zhu Xiping, Университет Сунь Ятсенa, Huai-Dong Cao, Lehigh University; 3) John Morgan, Колумбийский университет, Gang Tian, Массачусетский технологический институт. Все три группы пришли к выводу, что Проблема Пуанкаре успешно решена, однако китайские математики, Zhu Xiping и Huai-Dong Cao вместе со своим учителем Яу Шинтаном заявили, что они нашли «полное доказательство». От этого заявления они в дальнейшем отказались[11].
В декабре 2005 года Григорий Перельман ушёл с поста ведущего научного сотрудника лаборатории математической физики, уволился из ПОМИ[12] и практически полностью прервал контакты с коллегами[13].
К дальнейшей научной карьере интереса не проявлял. В настоящее время живёт в Купчино в одной квартире с матерью [14], ведёт замкнутый образ жизни, игнорирует прессу[15].
Научный вклад
В 1994 году доказал гипотезу о душе.
Будучи представителем ленинградской геометрической школы, развил и применил сугубо ленинградскую теорию пространств Александрова для анализа потоков Риччи. В 2002 году Перельман впервые опубликовал свою новаторскую работу[16], посвящённую решению одного из частных случаев гипотезы геометризации Уильяма Тёрстона[17], из которой следует справедливость знаменитой гипотезы Пуанкаре, сформулированной французским математиком, физиком и философом Анри Пуанкаре в 1904 году. Описанный учёным метод изучения потока Риччи получил название теории Гамильтона — Перельмана[18].
Признание и оценки
В 1996 году был удостоен премии Европейского математического общества для молодых математиков, но отказался её получать[19]
В 2006 году Григорию Перельману за решение гипотезы Пуанкаре присуждена международная премия «Медаль Филдса», однако он отказался и от неё.
В 2006 году журнал Science назвал доказательство теоремы Пуанкаре научным прорывом года (англ. Breakthrough of the Year)[20]. Это первая работа по математике, заслужившая такое звание.
В 2006 году Сильвия Назар и Дэвид Грубер опубликовали статью «Manifold Destiny», которая рассказывает о Григории Перельмане, его работе по решению Проблемы Пуанкаре, этическим принципам в науке и математическом сообществе, а также содержит редкое интервью с ним самим. В статье уделено немалое место критике китайского математика Яу Шинтана, который вместе со своими учениками пытался оспорить полноту доказательства Гипотезы Пуанкаре, предложенного Григорием Перельманом[21]. Из интервью Григория Перельмана:
| Чужаками считаются не те, кто нарушает этические стандарты в науке. Люди подобные мне — вот кто оказывается в изоляции. [22] |
В 2006 году известная газета The New York Times опубликовала статью Дениса Овербая (Dennis Overbye) «Scientist at Work: Shing-Tung Yau. The Emperor of Math». Статья посвящена биографии профессора Яу Шинтана и скандалу, связанному с обвинениями в его адрес в попытках умалить вклад Перельмана по доказательству Гипотезы Пуанкаре. В статье приводится неслыханный в математической науке факт — Яу Шинтан нанял адвокатскую фирму для защиты своей правоты и угрожал судебным преследованием своим критикам[23].
В 2007 году британская газета The Daily Telegraph опубликовала список «Сто ныне живущих гениев», в котором Григорий Перельман занимает 9-е место. Кроме Перельмана в этот список попали всего лишь 2 россиянина — Гарри Каспаров (25-е место) и Михаил Калашников (83-е место)[24].
В марте 2010 года Математический институт Клэя присудил Григорию Перельману премию в размере одного миллиона долларов США за доказательство гипотезы Пуанкаре
| Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой.[26] |
В сентябре 2011 года институт Клэя совместно с институтом Анри Пуанкаре (Париж) учредили должность для молодых математиков, деньги на оплату которой пойдут из «Премии тысячелетия»[27]. В 2011 году Ричарду Гамильтону и Деметриосу Кристодулу была присуждена т. н. Shaw Prize (англ.) по математике в размере $1 000 000, которую также иногда называют Нобелевской Премией Востока. Ричард Гамильтон был награждён за создание математической теории, которую затем развил Григорий Перельман в своих работах по доказательству гипотезы Пуанкаре. Известно, что Гамильтон данную награду принял.[28]
Интересные факты
| Если они знают мои работы, им не нужно мое C.V. Если они нуждаются в моем C.V., они не знают мои работы.[31] |
- Статья Manifold Destiny была замечена выдающимся математиком Владимиром Арнольдом, предложившем перепечатать ее в московском журнале «Успехи математических наук», где он был членом редколлегии. Главный редактор журнала Сергей Новиков ответил ему отказом. По мнению Арнольда, отказ был связан с тем, что главный редактор журнала опасался мести со стороны Яу, так как тоже работал в США.[32]
- О судьбе Перельмана повествует биографическая книга Маши Гессен «Совершенная строгость. Григорий Перельман: гений и задача тысячелетия»[33], основанная на многочисленных интервью с его учителями, одноклассниками, сослуживцами и коллегами[34].
- Григорий Перельман стал главным действующим лицом документального фильма «Чары гипотезы Пуанкаре» режиссёра Масахито Касуги, снятого японской общественной телерадиокомпанией NHK в 2008 году.
- В Николаеве на улице Советской в политической рекламе использовали фотографию Григория Перельмана для образа пенсионера с текстом: «А мне пенсию подняли на 7 гривень! 31 октября проголосую за регионалов или за Тигипко»[35].
- В апреле 2010 года выпуск «Миллионер из хрущоб»[36] ток-шоу «Пусть говорят» был посвящён Григорию Перельману. В нём принимали участие друзья Григория, его школьные учителя, а также журналисты, которые общались с Перельманом.
- В 27-м выпуске Большой разницы на Первом канале была представлена пародия в зале на Григория Перельмана. Роль Перельмана одновременно исполняли 9 актёров.
- Распространено заблуждение, что отцом Григория Яковлевича Перельмана является Яков Исидорович Перельман — известный популяризатор физики, математики и астрономии[37]. Однако Я. И. Перельман умер более чем за 20 лет до рождения Григория Перельмана.
- 28 апреля 2011 года «Комсомольская правда» сообщила, что Перельман дал интервью исполнительному продюсеру московской кинокомпании «Президент-фильм» Александру Забровскому и согласился на съёмки о нём художественного фильма[38]. Маша Гессен, однако, сомневается в том, что эти утверждения соответствуют действительности[39]. Владимир Губайловский также считает, что интервью с Перельманом является вымышленным[40].
- 15 июня 2011 года на канале «Россия» вышел документальный фильм «Иноходец. Урок Перельмана», рассказывающий о жизни и научной деятельности Г. Перельмана.
- В апреле 2012 года на кинофестивале «Трайбека» был представлен короткометражный художественный фильм «Хроноглаз», основанный на истории Григория Перельмана. Режиссёр Алексей Федорченко[41].
Примечания
- ↑ Гипотеза Пуанкаре, Clay Mathematics Institute (англ.)
- ↑ Найти Перельмана // Gazeta.Ru, 17 августа 2006
- ↑ Перельман, Григорий. Российский математик, доказавший гипотезу Пуанкаре, Lenta.ru, 07.09.2009.
- ↑ Grigorij Perelman (англ.) на сайте IMO
- ↑ bbcrussian.com, 22 августа 2006 г.
- ↑ Perelman, Grisha (November 11, 2002), «The entropy formula for the Ricci flow and its geometric applications», arΧiv:math.DG/0211159 [math.DG]
- ↑ Perelman, Grisha (March 10, 2003), «Ricci flow with surgery on three-manifolds», arΧiv:math.DG/0303109 [math.DG]
- ↑ Perelman, Grisha (July 17, 2003), «Finite extinction time for the solutions to the Ricci flow on certain three-manifolds», arΧiv:math.DG/0307245 [math.DG]
- ↑ См. Manifold Destiny
- ↑ См. John Morgan, Gang Tian. Ricci Flow and the Poincare Conjecture. American Mathematical Society. Clay Mathematical Institute. Clay Mathematics Monographs. Vol. 3, 2007. Introduction, p.XL.
- ↑ См. Manifold Destiny
- ↑ О причинах ухода Г. Перельмана из ПОМИ. Интервью с директором ПОМИ С. В. Кисляковым.
- ↑ Nasar, Sylvia, Gruber, David. Manifold Destiny: A legendary problem and the battle over who solved it., The New Yorker (21 August 2006). Проверено 24 августа 2006.
- ↑ Перельман: Насчет $ 1 млн я ещё не решил!. LifeNews.Ru
- ↑ Первые контакты с Григорием Перельманом
- ↑ Grisha Perelman The entropy formula for the Ricci flow and its geometric applications (англ.), Ricci flow with surgery on three-manifolds (англ.).
- ↑ Weisstein, Eric W. Thurston’s Geometrization Conjecture (англ.) на сайте Wolfram MathWorld.
- ↑ Ю. Грановский Вселенские поиски Перельмана. Что такое гипотеза Пуанкаре и почему питерскому ученому дали математическую «Нобелевку» и хотят добавить миллион долларов // Ведомости. — В. 25.08.2006.
- ↑ О. Орлова Перельман — это замкнутая сфера. Мы не можем в него заглянуть… // Троицкий Вариант. — 2010 . — № 52. — С. 5.
- ↑ Dana Mackenzie (2006). «BREAKTHROUGH OF THE YEAR: The Poincaré Conjecture—Proved». Science 314 (5807): 1848-1849. DOI:10.1126/science.314.5807.1848. (англ.)
- ↑ Сильвия Насар, Дэвид Грубер «Многообразная судьба: Легендарная задача и битва за приоритет». Перевод статьи «Manifold Destiny».
- ↑ См. перевод статьи Manifold Destiny
- ↑ The Emperor of Math
- ↑ Top 100 living geniuses. telegraph.co.uk (31.01.2007). Архивировано из первоисточника 16 февраля 2012. (англ.)
- ↑ Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman (англ.). Пресс-релиз математического института Клэя. 18.03.2010
- ↑ Последнее «нет» доктора Перельмана.
- ↑ Миллион долларов Перельмана отдадут на поддержку молодых математиков. Интерфакс (22 сентября 2011 года). Проверено 22 сентября 2011.
- ↑ [1] [2]
- ↑ См. The entropy formula for the Ricci flow and its geometric applications
- ↑ В июле 2004 года Национальный научный фонд США выделил $1 000 000 Яу Шинтану, Ричарду Гамильтону и нескольким ученикам Яу для изучения результатов Перельмана. См. [Manifold Destiny]
- ↑ См. Manifold Destiny
- ↑ «Опасаться компетентных соперников очень естественно для начальников», интервью Владимира Арнольда изданию GZT.ru (Опубликовано посмертно).
- ↑ Маша Гессен Совершенная строгость. Григорий Перельман: гений и задача тысячелетия. — АСТ, Corpus, 2011. — 272 с. — ISBN 978-5-271-33232-6
- ↑ С. Немалевич Теорема о Перельмане: интервью с Машей Гессен о книге про великого олимпиадника // Theory & Practice. — 12 апреля 2011.
- ↑ Российского математика Перельмана превратили в николаевского бомжа // for-ua.com, 15 октября 2010
- ↑ Пусть говорят — Миллионер из хрущоб. Выпуск от 30 апреля 2010.
- ↑ О. Волкова Занимательный Перельман. MK.ru (24.08.06). Архивировано из первоисточника 16 февраля 2012.
- ↑ А. Велижагина. Интервью с математиком Григорием Перельманом: Зачем мне миллион долларов? Я могу управлять Вселенной
- ↑ М. Гессен. 6 странных ошибок в «интервью Перельмана»
- ↑ Владимир Губайловский. Слезы «Комсомолки». Экспертиза интервью «Григория Перельмана»
- ↑ Газета «Санкт-Петербургские ведомости» от 27 марта 2012 года
Литература
- 2011 г. Маша Гессен. Совершенная строгость. Григорий Перельман. Гений и задача тысячелетия. (A Genius and The Mathematical Breakthrough of the Century). Издательства Corpus, Астрель, переводчик Илья Кригер, 272 с., тираж 4000 экз., ISBN 978-5-271-33232-6
- 2010 г. Олег Арсенов. Григорий Перельман и гипотеза Пуанкаре. Издательство Эксмо, серия Люди науки, 256 с., тираж 3000 экз., ISBN 978-5-699-44145-7
- George G. Szpiro, Poincare’s Prize: The Hundred-Year Quest to Solve One of Math’s Greatest Puzzles. Dutton Adult[3]; 1st edition (June 21, 2007)
Ссылки
dic.academic.ru
многомерная фигура — Naked Science
В основе курса СССР на точные науки, подготовившего почву для достижений ядерной физики, космонавтики и спортивных шахмат, лежала сильная математическая традиция. Оформившись в 1930-х, она подарила миру таких ученых, как Андрей Колмогоров, Александр Гельфонд, Павел Александров и многих других, которые преуспели в традиционных (алгебра, теория чисел) и новых направлениях математики (топология, теория вероятностей, математическая статистика). По масштабам интересов и интеллектуальных ресурсов сравниться с советской могли разве что американская и китайская школы. Но сравнением они не ограничивались: на макроуровне царица наук развивалась в противоречивой обстановке дружелюбной подозрительности. Важную роль такие взаимовлияния сыграли и в профессиональной жизни Григория Перельмана – признанного математического гения, окончательно доказавшего гипотезу Пуанкаре и решившего таким образом одну из семи «задач тысячелетия».
Сurriculum vitæ. Первые страницы
Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде в семье инженера-электрика и учительницы математики, а спустя десять лет у него появилась сестра – в будущем тоже кандидат (точнее, PhD) математических наук. Помимо любви к классической музыке, привитой матерью, Григорий с детства проявлял интерес к точным наукам: в пятом классе он начал посещать математический центр при Дворце пионеров, а после восьмого перешел в школу № 239 с углубленным изучением математики, которую окончил без золотой медали только из-за недостатка баллов по нормативам ГТО. В 1982 году он в составе школьной команды получил золотую медаль на 23-й Международной математической олимпиаде в Будапеште и вскоре был зачислен на математико-механический факультет Ленинградского государственного университета без сдачи экзаменов.
В вузе за примерную учебу Перельман получал Ленинскую стипендию. Окончив университет с отличием, он поступил в аспирантуру на базе Ленинградского отделения Математического института имени В. А. Стеклова РАН. В 1990 году под научным руководством академика Александра Даниловича Александрова (основоположника так называемой геометрии Александрова – раздела метрической геометрии) Перельман защитил кандидатскую диссертацию на тему «Седловые поверхности в евклидовых пространствах». Затем в должности старшего научного сотрудника продолжил работать в лаборатории математической физики института Стеклова, успешно развивая теорию пространств Александрова.
В начале 1990-х Перельману довелось поработать в нескольких уважаемых исследовательских учреждениях США: в Университете штата Нью-Йорк в Стоуни-Брук, Курантовском институте математических наук и Калифорнийском университете в Беркли.

Поворотной для молодого математика стала встреча с Ричардом Гамильтоном, область научных интересов которого простиралась в плоскости дифференциальной геометрии – нового направления, широко используемого в общей теории относительности. В своих работах по топологии многообразий американский ученый впервые использовал систему дифференциальных уравнений под названием поток Риччи – нелинейный аналог уравнения теплопроводности, который описывает не распределение температуры, а деформацию хаусдорфова пространства, локально эквивалентного евклидовому.
Благодаря этой системе уравнений Гамильтону удалось наметить решение одной из семи «задач тысячелетия» – по сути, разработать подход к доказательству гипотезы Пуанкаре.
Благосклонность зарубежного коллеги и столь фундаментальная проблема произвели на Перельмана большое впечатление. В то время он продолжал сглаживать углы пространств Александрова – технические трудности казались непреодолимыми, и ученый вновь и вновь возвращался к идее потока Риччи. По словам советского математика Михаила Громова, сосредоточившись на этих задачах, Перельман стал еще более аскетичным, что вызывало тревогу у его близких.
В 1994 году он получил приглашение прочесть лекцию на Международном конгрессе математиков в Цюрихе, а сразу несколько научных организаций, в том числе Принстонский и Тель-Авивский университеты, предложили ему место в штате. В ответ на просьбу Стэнфордского университета предоставить резюме и рекомендации ученый заметил: «Если они знают мои работы, им не нужно мое CV. Если же они нуждаются в моем CV, они не знают мои работы». Несмотря на такое обилие заманчивых предложений, в 1995 году он принял решение вернуться в «родной» институт Стеклова.
В 1996-м Европейское математическое общество присудило Перельману его первую международную премию, которую по каким-то причинам он отказался получать.
Помимо непритязательности в быту, пристрастия к музыке (Перельман играет на скрипке) и строгой приверженности научной этике, ученого уже тогда отличал интерес к параллельному решению сложных задач. В 1994 году он доказал гипотезу о душе. В дифференциальной геометрии под «душой» (S) подразумевают компактное тотально выпуклое тотально геодезическое подмногообразие риманова многообразия (M, g). В простейшем случае, то есть в случае евклидова пространства Rn (n отражает мерность), душой будет любая точка этого пространства.
Перельман доказал, что душа полного связного риманова многообразия с секционной кривизной K ≥ 0, секционная кривизна одной из точек в котором строго положительна во всех направлениях, является точкой, а само многообразие диффеоморфно Rn. Математиков потрясло редкостное изящество доказательства Перельмана: выкладки заняли всего две страницы, в то время как «доперельмановские» попытки решения излагались в длинных статьях и оставались незавершенными.
Доказательство гипотезы Пуанкаре, или Благодатное слияние кухни с операционной
На рубеже 19–20 веков гениальный французский математик Анри Пуанкаре увлеченно закладывал фундамент топологии – науки о свойствах пространств, которые остаются неизменными при непрерывных деформациях. В 1900 году ученый предположил, что трехмерное многообразие, все группы гомологий которого как у сферы, гомеоморфно сфере (топологически ей эквивалентно). В общем же случае, для многообразий любой мерности, гипотеза звучит примерно так: всякое односвязное замкнутое n-мерное многообразие гомеоморфно n-мерной сфере. Здесь необходимо хоть немного расшифровать термины, которыми так свободно оперировал Пуанкаре.
Электронная модель преобразования Пуанкаре – Перельмана
Двумерное многообразие – это плоскость: например, поверхность сферы или тора («бублика»). Трехмерное многообразие представить сложнее: в качестве одной из его моделей рассматривают додекаэдр, противоположные грани которого особым образом «склеены» друг с другом – отождествлены. Именно для случая трехмерного многообразия гипотеза Пуанкаре оставалась крепким орешком на протяжении целого века. Что касается гомеоморфизма, то любые замкнутые, без дыр, поверхности гомеоморфны, то есть могут непрерывно и однозначно преобразовываться (отображаться) друг в друга и деформироваться в сферу, а вот с тором, например, такое без разрыва поверхности не пройдет, поэтому он негомеоморфен сфере, зато гомеоморфен… кружке – той самой, из кухонного шкафчика. Гомология – понятие, позволяющее строить специфические алгебраические объекты (группы, кольца) для изучения топологических пространств – считается, что общеалгебраические структуры устроены проще, чем топологические. Вот простейшие примеры гомологии: замкнутая линия на поверхности гомологична нулю, если она служит границей какого-то участка этой поверхности; гомологичной нулю является любая замкнутая линия на сфере, у тора же такая линия может и не быть гомологичной нулю.

Мир, запутанный в суперструны
Группы – разнообразные множества, удовлетворяющие особым условиям, – оказались крайне полезными для описания топологических инвариантов – характеристик пространства, не меняющихся при его деформациях. Очень востребованы, в частности, группы гомологий и фундаментальные группы. Группа гомологии ставится в соответствие топологическому пространству для алгебраического исследования его свойств. Фундаментальная группа – это множество закрепленных (начинающихся и заканчивающихся) в отмеченной точке отображений отрезка в пространство (петель), измеряющих количество «дырок» в этом пространстве («дырки» возникают из-за невозможности непрерывно деформировать отрезок в точку). Такая группа представляет собой один из топологических инвариантов: гомеоморфные пространства имеют одну и ту же фундаментальную группу.

Проективный образ квазизамкнутого мира квантового вакуума с многосвязной топологией Пуанкаре – Перельмана
В первоначальном варианте гипотеза Пуанкаре для трехмерных многообразий оставалась «разрешимой»: она позволяла ослабить условие на фундаментальную группу до условия на группу гомологий. Однако вскоре Пуанкаре исключил это допущение, продемонстрировав пример нестандартной трехмерной гомологической сферы с конечной фундаментальной группой – «сферу Пуанкаре». Такой объект мог быть получен, например, склеиванием каждой грани додекаэдра с противоположной, повернутой на угол π/5 по часовой стрелке. Уникальность сферы Пуанкаре заключается в том, что она гомологична трехмерной сфере, но при этом отличаться от нее в евклидовом пространстве.
В окончательной формулировке гипотеза Пуанкаре звучала следующим образом: всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере. Доказательство этой гипотезы сулило новые возможности для моделирования многомерных пространств. В частности, полученные с помощью космического зонда WMAP данные позволяли рассматривать додекаэдрическое пространство Пуанкаре как возможную математическую модель формы Вселенной.
И вот, в 2002–2003 годах (к тому моменту тематическая переписка Перельмана с Гамильтоном уже сошла на нет) пользователь с ником Grisha Perelman с интервалом в несколько месяцев разместил на сервере препринтов arXiv.org три статьи (1, 2, 3), содержащие решение задачи, еще более общей, чем гипотеза Пуанкаре, – гипотезы геометризации Терстона. И первая же публикация стала международной научной сенсацией, хотя из-за антипатии автора к бюрократии ни одна из статей так и не попала на страницы рецензируемых журналов. Выкладки Перельмана были настолько лаконичны и в то же время сложны, что во всеобщий восторг просто не могло не вкрасться недоверие, поэтому с 2004 по 2006 годы проверку работ Перельмана проводили сразу три группы ученых из США и Китая.
В глубине Мироздания: переплетение мембран, фридмонов и максимонов
Чтобы деформировать риманову метрику на односвязном трехмерном многообразии до гладкой метрики целевого многообразия, Перельман ввел новый метод изучения потока Риччи, который вполне справедливо назвали теорией Гамильтона – Перельмана. Изюминка метода заключалась в том, чтобы при подходе к сингулярности, возникающей при деформации метрики, остановить применяемый к многообразию поток и вырезать «шею» (открытую область, диффеоморфную прямому произведению) или выбросить малую связную компоненту, «заклеив» две полученные «дырки» шарами. По мере повторения этой хирургической операции выбрасывается все, при этом каждый кусок диффеоморфен сферической пространственной форме, а итоговое многообразие является сферой.
В итоге Перельману удалось не только доказать гипотезу Пуанкаре, но и полностью классифицировать компактные трехмерные многообразия. Вероятно, этого никогда бы не случилось, если бы в длинном списке отличительных черт Перельмана не значилась непоколебимая настойчивость. Бывший учитель математики, кандидат физико-математических наук Сергей Рушкин вспоминал: «Гриша начал очень много работать в девятом классе, и у него оказалось очень ценное для занятий математикой качество: способность к очень длительной концентрации внимания без особых успехов внутри задачи.
Все-таки человеку нужна психологическая подпитка, нужны психологические успехи, чтобы заниматься чем-то дальше. Фактически гипотеза Пуанкаре – это почти девять лет без знания того, решится задача или не решится. Понимаете, там даже невозможны были частичные результаты. Не доказалась теорема в полном объеме – иной раз можно опубликовать даже двадцатистраничную статью по тому, что все-таки получилось. А там – или пан, или пропал».
Вечность в кармане
В 2003 году Григорий Перельман принял приглашение прочесть о своих работах серию публичных лекций и докладов в США. Но его не понимали ни студенты, ни коллеги. В течение нескольких месяцев математик терпеливо объяснял, в том числе и в личных беседах, свои методы и идеи. Во время «американского турне» Перельман рассчитывал и на плодотворный разговор с Гамильтоном, но он так и не состоялся. Вернувшись в Россию, ученый продолжил отвечать на сыпавшиеся от математиков вопросы по электронной почте.
В 2005 году, устав от атмосферы публичности, интриг и бесконечных объяснений, связанных с затянувшейся проверкой его выкладок, Перельман уволился из института и фактически оборвал профессиональные связи.
В 2006 году все три группы экспертов признали доказательство гипотезы Пуанкаре состоявшимся, на что китайские математики во главе с Яу Шинтуном, чья фамилия красуется в названии целого класса многообразий (пространств Калаби–Яу), ответили попыткой оспорить приоритет Перельмана. Правда, выбранный для этого инструментарий оказался неудачным: он сильно походил на плагиат. Оригинальная статья учеников Яу, Цао Хуайдуна и Чжу Сипина, занявшая весь июньский номер The Asian Journal of Mathematics, аннотировалась как окончательное доказательство гипотезы Пуанкаре с применением теории Гамильтона – Перельмана. Если верить журналистским расследованиям, то еще перед публикацией этой статьи, открыто курируемой Яу, последний потребовал у 31 математика из редколлегии журнала в кратчайшие сроки прокомментировать ее, однако саму статью тогда почему-то не предоставил.
Яу Шинтун не просто отлично знал Гамильтона, но и сотрудничал с ним, и заявление Перельмана об успешном решении задачи стало для обоих ученых сюрпризом: после долгих лет работы над ней они рассчитывали, несмотря на временную заминку, прийти к финишу первыми. Впоследствии Яу подчеркивал, что препринты Перельмана выглядели неряшливо и невнятно из-за отсутствия подробных расчетов (автор приводил их по мере необходимости в ответ на запросы независимых экспертов), и это мешало ему и всем остальным понять доказательство в полной мере.

Мир суперновой физики пространства-времени в теореме Пуанкаре – Перельмана
Попытка умалить заслуги Перельмана – а Яу даже любезно подсчитал их в процентном выражении – не удалась, и вскоре китайские ученые подкорректировали заглавие и аннотацию своей статьи. Теперь ее нужно было воспринимать не как свидетельство «венценосного достижения» китайских математиков, а как «самостоятельную и подробную экспозицию» доказательства гипотезы Пуанкаре, произведенного Гамильтоном и Перельманом – без посягательств на чей-то приоритет. Перельман прокомментировал действия Яу так: «Я не могу сказать, что я возмущен, остальные поступают еще хуже…» И правда, китайского математического гения можно понять: ревностную поддержку статьи своих учеников Яу позже объяснял желанием представить окончательное доказательство в удобоваримом, каждому понятном виде и закрепить в истории заслуги соотечественников в решении этой задачи тысячелетия – а ведь их и на самом деле отрицать нельзя…
Тем временем, в августе 2006 года, Перельману присудили Филдсовскую премию «за вклад в геометрию и его революционные идеи в изучении геометрической и аналитической структуры потока Риччи». Но, как и десять лет назад, от награды Перельман отказался, а заодно и сообщил о нежелании далее пребывать в статусе профессионального ученого. В декабре того же года журнал Science впервые признал математическую работу – работу Перельмана – «Прорывом года». Тогда же СМИ разразились серией статей, освещающих это достижение, правда, с упором на сопровождавший его конфликт. Для защиты своей позиции Яу обратился к адвокатам и пригрозил судом «опорочившим его имя» журналистам, однако угрозу так и не осуществил.
В 2007 году Перельман занял девятое место в рейтинге «Сто ныне живущих гениев», опубликованном в The Daily Telegraph. А спустя три года Математический институт Клэя присудил за решение задачи тысячелетия «Премию тысячелетия» – впервые в истории. Поначалу премию в один миллион долларов Перельман проигнорировал, а затем официально отверг: «Если говорить совсем коротко, то главная причина – это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой».

Инфляционная экспансия в представлении многообразия Пуанкаре – Перельмана
В 2011 году «Премию тысячелетия», от которой отказался Перельман, Институт Клэя решил направить на оплату труда молодых, подающих надежды математиков, для которых в парижском Институте Анри Пуанкаре учредили специальную временную должность. Тогда же Ричарду Гамильтону присудили Премию Шао по математике за создание программы решения гипотезы Пуанкаре. Премиальный миллион долларов в тот год пришлось разделить поровну между Гамильтоном и вторым математическим лауреатом, Деметриосом Христодулу.
Доброе отношение к Гамильтону Перельман сохранил, несмотря на несостоявшийся диалог и очевидную неудовлетворенность старшего коллеги финалом этой научной истории. А это многое говорит о человеке. По слухам, Григорий Яковлевич продолжает жить в Санкт-Петербурге, периодически посещая Швецию, где сотрудничает с местной компанией, занимающейся научными разработками. Ну а шесть задач тысячелетия все еще ждут своего гения.
naked-science.ru
Что же доказал Григорий Перельман?
Сергей Дужин,
доктор физ.-мат. наук, старший научный сотрудник Санкт-Петербургского отделения Математического института РАН
«Троицкий вариант» №10(104), 22 мая 2012 года
Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3».
В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).
Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.
Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией.
Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).
Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы.
- Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R3 , а также любые открытые множества точек в R3 , к примеру внутренность полнотория (бублика). Если рассмотреть замкнутое полноторие, т. е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем — у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.
- Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, что то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы.
- Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.
- Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.
Размерность многообразия — это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т. е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т. д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна.
Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий — ведь у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка.
Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые1 многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности.
На рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно.
Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т. е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S3 выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S3 стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т. е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь.
Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R3, что облегчает их визуализацию. Для трехмерной сферы S3 (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение.
По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S3 — это при помощи одноточечной компактификации. А именно, трехмерная сфера S3 представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R3.
Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность — одномерный аналог сферы.
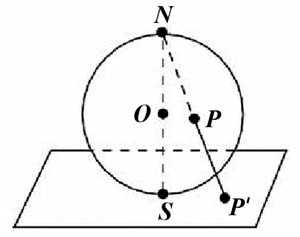
Подобным же образом, если я возьму бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S2 . Эту процедуру можно наблюдать при помощи стереографической проекции, которая каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P’.
Таким образом, сфера без одной точки — это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу.
В принципе, точно такая же конструкция применима и к трехмерной сфере и трехмерному пространству, только для ее осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. Поэтому я ограничусь словесным описанием одноточечной компактификации пространства R3.
Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т. е. каждая пространственная прямая замыкается в окружность). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S3.
Легко понять, что сфера S3 односвязна. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R3, которая легко стягивается в точку посредством гомотетий, т. е. непрерывного сжатия по всем трем направлениям.
Для понимания, как устроено многообразие S3, весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R3 выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S3 разбивается на два полнотория, имеющих общую границу — тор.

Вот как это можно понять. Вложим тор в R3 как обычно, в виде круглого бублика, и проведем вертикальную прямую — ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет наше полноторие по двум кругам, показанным на рисунке зеленым цветом, а дополнительная часть плоскости разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, выделенная более жирно, потому что в сфере S3 прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомеоморфное полноторию, только выглядящее необычно.
В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей — окружностей, составляющих обычное полноторие.
Чтобы было с чем сравнивать 3-сферу, я приведу еще один пример компактного 3-многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб:
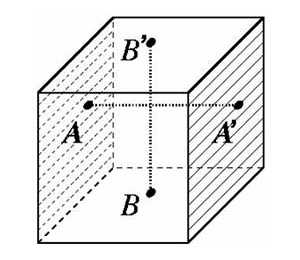
В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A’ — это одна и та же точка, а B и B’ — тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб — это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A’ в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора.
Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх — и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления. Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная.
На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA’ на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A’ обязаны двигаться по своим граням, оставаясь строго друг напротив друга (иначе кривая разомкнется).
Итак, мы видим, что бывают односвязные и неодносвязные компактные 3-многообразия. Перельман доказал, что односвязное многообразие ровно одно.
Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т. е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, — в трехмерном случае поток Риччи способен портить многообразие, т. е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, а в конце концов, оно превращается в круглую сферу. Но нужно объяснить, наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому я ограничусь описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость.
Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она более плавная, кривизна будет меньше.
Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение не зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например, окружность радиуса 1 имеет постоянную положительную кривизну, равную 1 (если считать ее в радианах).
Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот пример:
Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т. е. превращается, в конце концов, в окружность. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, просто способ доказательства иллюстрирует, что происходит в размерности 3).
Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и гораздо более общую гипотезу геометризации Тёрстона, которая в известном смысле описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи.
1 За неимением места, я не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна — поверхность, которую нельзя вложить в пространство без самопересечений.
elementy.ru
«Гениев осуждать нельзя». Как живет математик Григорий Перельман | наука | ОБЩЕСТВО
11 ноября 2002 года на одном из крупных порталов научных публикацией в интернете появилась статья петербургского математика Григория Перельмана, в которой он приводил доказательства гипотезы Пуанкаре. Таким образом, гипотеза стала первой решенной задачей тысячелетия – так называют математические вопросы, ответы на которые не могут найти уже много лет. Восемь лет спустя Математический институт Клэя присудил ученому за это достижение премию в размере одного миллиона долларов США, но Перельман отказался от нее, заявив, что не нуждается в деньгах и, кроме того, не согласен с официальным математическим сообществом. Отказ небогатого математика от крупной суммы вызвал удивление во всех слоях общества. За это и за свой затворнический образ жизни Перельмана называют самым странным российский ученым. SPB.AIF.RU узнал, как сегодня живет и чем занимается Григорий Перельман.
Математик №1
Сейчас Григорию Перельману 51 год. Ученый ведет замкнутый образ жизни: он практически не выходит из дома, не дает интервью и нигде официально не трудоустроен. У математика никогда не было близких друзей, но люди, которые знакомы с Перельманом, утверждают: он был таким не всегда.«Я помню Гришу еще подростком, – рассказывает сосед Перельмана по дому, Сергей Краснов. – Хотя мы живем на разных этажах, видимся иногда. Раньше могли побеседовать с его мамой, Любовью Лейбовной, но теперь я ее редко встречаю. Они с Григорием периодически выходят прогуляться, а так постоянно дома. Когда увидимся – кивнут быстро и идут дальше. Ни с кем не общаются. А в школьные годы Гриша ничем не отличался от других мальчишек. Конечно, он уже тогда активно интересовался наукой и много сидел за книгами, но и на другие дела время находил. Учился музыке, гулял с друзьями, спортом занимался. А потом принес все свои интересы в жертву математике. Стоило ли оно того? Не знаю».
Григорий всегда занимал первые мест на олимпиадах по математике, но однажды победа ускользнула от него: в восьмом классе на Всесоюзной олимпиаде Перельман стал только вторым. С тех пор он отказался от всех своих хобби и отдыха, с головой погрузившись в книги, справочники и энциклопедии. Вскоре он наверстал упущенное и стал молодым математиком №1 в стране.
Затворничество
Краснов заявляет: никто из жильцов их дома не сомневался, что Перельман станет великим ученым. «Когда мы узнали, что Гриша доказал гипотезу Пуанкаре, чего не мог сделать ни один человек в мире, мы даже не удивились, – признается пенсионер. – Конечно, очень обрадовались за него, решили: наконец-то Григорий пробьется в люди, сделает головокружительную карьеру! Молодец, ведь он это заслужил! Но он выбрал для себя другой путь».
Перельман отказался от денежной премии в размере миллиона долларов, обосновав свое решение несогласием с официальном математическим сообществом, при этом добавив, что в деньгах не нуждается.
После того, как имя Перельмана прогремело на весь мир, математика пригласили в США. В Америке ученый выступал с докладами, обменивался опытом с зарубежными коллегами и объяснял свои методы решения математических задач. Публичность быстро наскучила ему. Вернувшись в Россию, Перельман добровольно покинул пост ведущего научного сотрудника лаборатории математической физики, уволился из петербургского отделения Математического института имени Стеклова РАН и свел свое общение с коллегами к нулю. Несколько лет спустя Перельмана хотели сделать членом Российской академии наук, но тот отказался. Прекратив практически все контакты с внешним миром, ученый заперся в своей квартире в Купчино, на окраине Петербурга, где живет вместе с мамой.
«Гришу замучили вниманием»
Сейчас математик очень редко выходит из дома и целые дни проводит за решением новых задач. «Гриша с мамой живут на одну пенсию Любови Лейбовны, – рассказывает Краснов. – Мы, жильцы дома, ни в коем случае не осуждаем Гришу – мол, мужчина в расцвете сил, а денег в семью не приносит, старой матери не помогает. Такого нет. Он – гений, а гениев осуждать нельзя. Как-то раз даже хотели скинуться всем домом, материально помочь им. Но они отказались – сказали, что им хватает. Любовь Лейбовна всегда говорила, что Гриша неприхотлив: куртки или ботинки носит десятилетиями, а на обед ему достаточно макарон с сыром. Ну, не надо, так не надо».По мнению соседей, любой человек на месте Перельмана стал бы нелюдимым и закрытым: хотя математик уже давно не дает поводов для обсуждения, его персону до сих пор не могут оставить без внимания. «Некоторые журналисты сутки напролет дежурят под дверью Перельмана, – возмущается Сергей Петрович. – Один раз дождались, когда Гриша с мамой выходили из квартиры на прогулку. Здоровенный оператор буквально смел Любовь Лейбовну, чтобы снять обстановку в их квартире – у них не очень убрано, и на этим решили сакцентировать внимание. А молодая корреспондент набросилась на самого Перельмана с вопросами. Они после этого долго никуда не выходили. Тут у всякого стресс будет! Гришу замучили вниманием!».
Жильцы дома уверены, что Перельман еще заявит о себе, сделав новое открытие в области математики. «Его труды даром не пропадут, – считает Краснов. – Просто нужно не трогать его и дать спокойно жить».
spb.aif.ru
Сказка о математике Григории Перельмане, который решил одну из семи задач тысячелетия
Ник. Горькавый
«Наука и жизнь» №8, 2018
Другие научные сказки Ник. Горькавого см. в «Науке и жизни» №11, 2010, №12, 2010, №1, 2011, №2, 2011, №3, 2011, №4, 2011, №5, 2011, №6, 2011, №9, 2011, №11, 2011, №6, 2012, №7, 2012, №8, 2012, №9, 2012, №10, 2012, №12, 2012, №1, 2013, №11, 2013, №1, 2014, №2, 2014, №3, 2014, №7, 2014, №8, 2014, №10, 2014, №12, 2014, №1, 2015, №4, 2015, №5, 2015, №6, 2015, №7, 2015, №9, 2015, №1, 2016, №2, 2016, №3, 2016, №6, 2016, №8, 2016, № 11, 2016, № 2, 2017, № 4, 2017, № 6, 2017, № 7, 2017, №10, 2017, №12, 2017, №7, 2018.
Журнальный вариант одной из глав новой книги Ник. Горькавого «Неоткрытые миры» (СПб.: «Астрель», 2018).

Математики — люди особенные. Они так глубоко погружаются в абстрактные миры, что, «возвращаясь на Землю», часто не могут приспособиться к реальной жизни и удивляют окружающих непривычными взглядами и поступками. У нас речь пойдёт о едва ли не самом талантливом и неординарном из них — Григории Перельмане.
В 1982 году шестнадцатилетний подросток Гриша Перельман, только что получивший золотую медаль на Международной математической олимпиаде в Будапеште, поступил в Ленинградский университет. Он заметно отличался от других студентов. Его научный руководитель профессор Юрий Дмитриевич Бураго рассказывал: «Существует масса одарённых студентов, которые говорят раньше, чем думают. Гриша был не таким. Он всегда очень тщательно и глубоко обдумывал, что намеревался сказать. Он не был очень быстрым в решениях. Скорость решения не значит ничего, математика не построена на скорости. Математика зависит от глубины».
После окончания университета Григорий Перельман стал сотрудником Математического института имени Стеклова, опубликовал ряд интересных статей по трёхмерным поверхностям в евклидовых пространствах. Мировое математическое сообщество оценило его достижения по заслугам. В 1992 году Перельмана пригласили на работу в Нью-Йоркский университет.
Григорий попал в один из мировых центров математической мысли. Каждую неделю он ездил на семинар в Принстон, где однажды прослушал лекцию выдающегося математика, профессора Колумбийского университета Ричарда Гамильтона. После лекции Перельман подошёл к профессору и задал несколько вопросов. Позже Перельман вспоминал об этой встрече: «Мне было очень важно расспросить его кое о чём. Он улыбался и был очень со мной терпелив. Он даже рассказал мне пару вещей, которые были им опубликованы только несколько лет спустя. Он, не задумываясь, делился со мной. Мне очень понравились его открытость и щедрость. Могу сказать, что в этом Гамильтон был не похож на большинство других математиков».

Перельман провёл в США несколько лет. Он ходил по Нью-Йорку в одном и том же вельветовом пиджаке, питался в основном хлебом, сыром и молоком и непрерывно работал. Его стали приглашать в самые престижные университеты Америки. Молодой человек выбрал Гарвард и тут столкнулся с тем, что ему категорически не понравилось. Комитет по приёму на работу потребовал от соискателя автобиографию и рекомендательные письма от других учёных. Реакция Перельмана была жёсткой: «Если они знают мои работы, то им не нужна моя биография. Если им нужна моя биография, то они не знают моих работ». Он отказался от всех предложений и летом 1995 года вернулся в Россию, где продолжил работу над идеями, которые развивал Гамильтон. В 1996 году Перельману присудили премию Европейского математического общества для молодых математиков, но он, не любивший никакой шумихи, отказался её принять.
Когда Григорий добился определённых успехов в своих исследованиях, он написал письмо Гамильтону, надеясь на совместную работу. Однако тот не ответил, и Перельману пришлось действовать дальше в одиночку. Но впереди его ждала мировая слава.
В 2000 году Математический институт Клэя опубликовал «список проблем тысячелетия», в который вошли семь классических задач математики, решения которых не могут найти уже очень много лет, и пообещал премию миллион долларов за доказательство любой из них. Менее чем через два года, 11 ноября 2002-го, Григорий Перельман опубликовал на научном сайте в интернете статью, в которой на 39 страницах подвёл итог своих многолетних усилий по доказательству одной задачи из списка. Американские математики, которые знали Перельмана лично, немедленно принялись обсуждать статью, в которой доказывалась знаменитая гипотеза Пуанкаре. Учёного пригласили в несколько университетов США прочитать курс лекций, посвящённый его доказательству, и в апреле 2003 года он полетел в Америку. Там Григорий провёл несколько семинаров, на которых показывал, как ему удалось превратить гипотезу Пуанкаре в теорему. Математическое сообщество признало лекции Перельмана исключительно важным событием и предприняло значительные усилия по проверке предложенного доказательства.
Парадоксально, но Перельман не получал грантов для доказательства гипотезы Пуанкаре, а другим учёным, проверяющим его правильность, гранты на сумму миллион долларов были выделены. Проверка была крайне важна, ведь над доказательством этой задачи трудилось немало математиков, а если она действительно решена, то они оставались не у дел.
Математическое сообщество проверяло доказательство Перельмана несколько лет и к 2006 году пришло к выводу, что оно правильное. Юрий Бураго тогда писал: «Доказательство закрывает целую отрасль математики. После него многим учёным придётся переключиться на исследования в других областях».
Математика всегда считалась наукой максимально строгой и точной, где нет места эмоциям и интригам. Но даже здесь есть борьба за приоритет. Вокруг доказательства российского математика закипели страсти. Двое молодых математиков, выходцев из Китая, изучив работу Перельмана, опубликовали гораздо более объёмную и подробную — более трёхсот страниц — статью с доказательством гипотезы Пуанкаре. В ней они утверждали, что работа Перельмана содержит много пробелов, которые им удалось восполнить. Согласно правилам математического сообщества, приоритет в доказательстве теоремы принадлежит тем исследователям, которые сумели представить его в наиболее полном виде. По мнению многих специалистов, доказательство Перельмана было полным, хотя и кратко изложенным. Более подробные выкладки не вносили в него ничего нового.
Когда журналисты спросили Перельмана, что он думает о позиции китайских математиков, Григорий ответил: «Я не могу сказать, что я возмущён, остальные поступают ещё хуже. Разумеется, существует масса более или менее честных математиков. Но практически все они — конформисты. Сами они честны, но они терпят тех, кто таковыми не являются». Затем он с горечью отметил: «Чужаками считаются не те, кто нарушает этические стандарты в науке. Люди, подобные мне, — вот кто оказывается в изоляции».
В 2006 году Григорию Перельману присудили высшую награду в области математики — Филдсовскую премию. Но математик, ведущий уединённый, даже затворнический образ жизни, отказался её получать. Это был настоящий скандал. Президент Международного математического союза даже прилетал в Петербург и десять часов уговаривал Перельмана принять заслуженную награду, вручение которой планировалось на конгрессе математиков 22 августа 2006 года в Мадриде в присутствии испанского короля Хуана Карлоса I и трёх тысяч участников. Этот конгресс должен был стать историческим событием, однако Перельман вежливо, но непреклонно сказал: «Я отказываюсь». Филдсовская медаль, по словам Григория, его совершенно не интересовала: «Это не имеет никакого значения. Всем понятно, что если доказательство верное, то никакого другого признания заслуг не требуется».
В 2010 году Институт Клэя присудил Перельману обещанную премию в миллион долларов за доказательство гипотезы Пуанкаре, которую ему собирались вручить на математической конференции в Париже. Перельман отказался от миллиона долларов и в Париж не поехал.
Как объяснил он сам, ему не нравится этическая атмосфера в математическом сообществе. Кроме того, вклад Ричарда Гамильтона он считал ничуть не меньшим. Лауреат многих математических премий, советский, американский и французский математик М. Л. Громов поддержал Перельмана: «Для великих дел необходим незамутнённый разум. Ты должен думать только о математике. Всё остальное — людская слабость. Принять награду означает проявить слабость».
Отказ от миллиона долларов сделал Перельмана ещё более знаменитым. Многие просили его получить премию и отдать им. Григорий не отвечал на подобные просьбы.
До сих пор доказательство гипотезы Пуанкаре остаётся единственной решённой задачей из списка тысячелетия. Перельман стал математиком номер один в мире, хотя и отказался от контактов с коллегами. Жизнь показала, что выдающихся результатов в науке часто добивались одиночки, которые не входили в структуру современной науки. Таким был Эйнштейн. Работая клерком в патентном бюро, он создал теорию относительности, разработал теорию фотоэффекта и принцип работы лазеров. Таким стал Перельман, который пренебрёг правилами поведения в научном сообществе и достиг при этом максимальной эффективности своей работы, доказав гипотезу Пуанкаре.
Математический институт Клэя (Кембридж, США) основан в 1998 году бизнесменом Лэндоном Клэйем и математиком Артуром Джеффи для увеличения и распространения математических знаний.
Премия Филдса за выдающиеся достижения в области математики присуждается с 1936 года.
elementy.ru