Овал и эллипс в чем разница: Чем отличается овал от эллипса
Чем отличается овал от эллипса
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Определение
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
 Эллипс к содержанию ↑
Эллипс к содержанию ↑Сравнение
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
к содержанию ↑Выводы TheDifference.ru
- Объём. Овал – более широкое понятие, в объём которого входит эллипс.
- Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Чем отличается овал от эллипса |
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Что такое овал и эллипс
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
Разница между овалом и эллипсом
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:
Объём. Овал – более широкое понятие, в объём которого входит эллипс.
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
что общего, в чём отличие эллипса от овала
В школе большинству из нас не раз объясняли, в чём отличие радиуса от диаметра, серной кислоты от соляной, эллипса от овала. Но прошли годы, и школьные знания, «слежавшись» под весом многолетней будничной рутины, по большей части позабылись. В рамках данной статьи мы попытаемся восполнить хотя бы один досадный пробел в знаниях и подробнее рассмотрим последний из приведённых примеров, научившись отличать овал от эллипса. Для начала обозначим ключевые определения.
Овал
Под овалом в геометрии понимается вытянутая замкнутая фигура правильной формы. Овал относится к двухмерным фигурам и обладает особыми свойствами. Само слово образовано от французского Ovale, которое, в свою очередь, имеет общие корни с латинской лексемой ovum, что в переводе означает «яйцо». Кривая этого геометрического объекта имеет с любой прямой не более двух общих точек.
Справка! Нельзя сказать, что человек, называющий данную геометрическую фигуру просто «кругом», абсолютно прав. На самом деле окружность (в которой, как мы знаем, все точки кривой равноудалены от центра) – это одна из множества вариаций овала.
Существует структурно более сложное понятие овала в инженерной графике. В этой отрасли науки данным термином обозначают фигуру, имеющую две оси симметрии и построенную при помощи сочетания четырёх участков кривых линий от двух радиусов. Эти участки подобраны таким образом, чтобы обеспечить «перетекание» от одного радиуса к другому без нарушения симметрии и контура фигуры. Если определять координаты точки, постоянно движущейся по линии овала, то она всегда будет находиться на одном из вышеописанных радиусов кривизны. Эти радиусы считаются «фиксированными».
Эллипс
У слова «эллипс» имеются греческие корни, наиболее близкие по переводу к словам «нехватка, недостаток, опущение». Чего же не хватает в эллипсе и что эта фигура вообще из себя представляет?
Эллипсом принято считать любую замкнутую кривую на плоскости, которая имеет четыре вершины в так называемых точках экстремума. Точки фокуса эллипса равноудалены от его вершин. Стороны эллипса будут симметричны, если разделить его в любом направлении прямой, проходящей через его центр. Впрочем, это правило действительно и для фигур овального типа.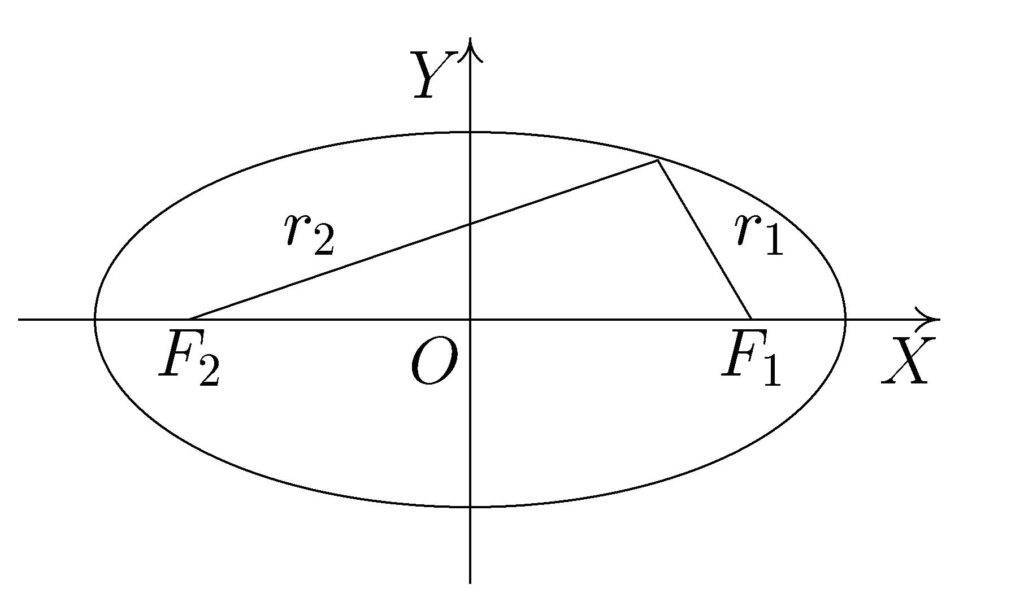
Что общего
Рассматривая вопрос о том, что может быть общего между овальной и эллиптической фигурой, можно заключить, что они имеют весьма похожий внешний вид. Кроме того, обе фигуры располагаются в так называемом евклидовом пространстве. На простом языке евклидово пространство можно объяснить как двумерное пространство, в котором положение точки может быть обозначено при помощи двух чисел, обозначающей её координаты.
В чём отличие эллипса от овала
Различия между двумя этими весьма смежными понятиями вытекают в основном из их определений. Вернувшись к рассмотренному нами определению овала в инженерной графике, можно заключить, что он, в отличие от эллипса, в котором радиус кривизны варьируется перманентно, обладает «фиксированными» радиусами.
Справка! В трёхмерном пространстве возможно построение объёмного овала. Такие фигуры называются эллипсоидами и способны иметь приплюснутую или вытянутую форму. Эта форма достаточно широко распространена в макромире: ею обладает огромное количество известных планет и даже галактики.
Для овальных фигур существует великое множество вариантов построения. Оси их, начинающиеся в точках своих вершин, имеют различные соотношения между собой. В случае же с эллиптическими фигурами в силу вступают особые правила построения. Говоря проще, овалом обозначают более общее понятие, а эллипсом – лишь одно из его проявлений.
геометрический овал с одной осью симметрии
3. Овал в инженерной графике
В инженерной графике под овалом обычно понимают фигуру с двумя осями симметрии, построенную на сочетании четырех участков кривых двух радиусов. Отрезки дуг выбраны так, что обеспечивается плавный переход от одного радиуса кривизны к другому. Точка, движется по периметру овала всегда находится на одном из двух фиксированных радиусов кривизны (в отличие от эллипса , где радиус кривизны постоянно меняется).
4. Овал в геометрии
Так же, как в обыденной речи, в геометрии математический термин «овал» встречается в названиях различных геометрических фигур более или менее овальной формы, но без точного определения овала как такового. Общее между этими кривыми, что это обычно кривые замкнутые, выпуклые, гладкие (с касательной в любой точке) и имеют по крайней мере одну ось симметрии.
Термин «овалоид» употребляют в яйцевидных поверхностей образованных вращением овальной кривой вокруг одной из ее осей симметрии.
Другие примеров овалов можно отнести.
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Определение
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс
Сравнение
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
Выводы сайт
- Объём. Овал – более широкое понятие, в объём которого входит эллипс.
- Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Фигура, представляющая собой объемный овал имеет следующее название — эллипсоид. Эллипсоиды могут иметь как вытянутую, так и приплюснутую форму.
Эллипсоид можно представить вот таким вот образом как на изображениях ниже:
А вот немного об этой фигуре:

Фигура, которая своей формой похожа на объмные овал, носит название quot;эллипсоидquot;. Источником для происхождения этого названия послужили два греческих слова:
Во Вселенной эта форма очень распространена: е имеют все планеты Солнечной системы, форма известных галактик также является эллиптической.
Если фигура напоминает объемный овал, скорее всего это перевернутые эллипс или эллипсоид.
А вот то, чем они различны.

Это эллипс, фигура изображенная на плоскости.

Это эллипсоид. Эллипс в пространстве и в объеме.
Скорее всего вы имеете в виду вот такую фигуру, как на фото ниже

своееобразное яйцо, ведь яйцо — это и есть овал. Такая фигура носит название вытянутый эллипсоид .
Эллипсоиды бывают и приплюснутые, они выглядит уже вот так:

Центр эллипосида лежит в начале координат. Эллипсоид имеет свою каноническую формулу:

В трхмерном пространстве объмная фигура, которая со стороны напоминает овал носит название — эллипсоид.
Если окунуться в мир формул, то основные параметры эллипсоида можно определить согласно следующим вычислениям:

Фигура, которая представляет собой объемный овал, называется эллипсоид . По форме эллипсоиды бывают вытянутые и приплюснутые. Самый наглядный пример приплюснутого эллипсоида — планета Земля, да и все остальные планеты Солнечной системы.

Если круг в объме, это шар, то овал в объме, это не что иное как эллипсоид. Примечательно, что данное слово пишется с двумя буквами quot;лquot;, поэтому не ошибитесь при написании.
Данная фигура мннее распространена, нежели куб или пирамила, и даже параллелепипед. Обычно в школе на уроках геометрии мы не так часто имеем дело с такими фигурами как эллипсоид. Оно и понятно, ведь правила и методы вычисления искомых значений в таких фигурах достаточно сложны.
Примером эллипсоида может служить спелый арбуз но не шарообразной формы, а именно немного вытянутой, то есть овальный в сечении. Есть и другие предметы в нашем обиходе. Часто в форм
Разница между Кругом и Эллипсом — Разница Между
Разница Между 2020
Ключевое отличие: Круг и Эллипс имеют замкнутые изогнутые формы. В круге все точки одинаково далеки от центра, что не относится к эллипсу; в эллипсе все точки находятся на разных расстояниях от центр
Содержание:
Ключевое отличие: Круг и Эллипс имеют замкнутые изогнутые формы. В круге все точки одинаково далеки от центра, что не относится к эллипсу; в эллипсе все точки находятся на разных расстояниях от центра.Математически круг является основной формой в области геометрии и ее определения: круг — это форма, в которой все точки находятся на одинаковом расстоянии от его центра. Он назван его центром. Некоторыми реальными примерами круга являются колеса, тарелка и (поверхность) монеты.
Слово ‘цирк’Происходит от греческого термина‘Киркос’, Который является метатезисом гомеровского греческого и означает‘обруч‘ или же ‘кольцо». Круг был известен еще до записи истории. Солнце и Луна являются естественными примерами круга, в то время как даже короткий стебель, дующий на ветру, образует форму круга в песке. Принцип круга был применен при формировании колес и механизмов доисторическим человеком. Сейчас, в современную эпоху, существует множество разновидностей механизмов, основанных на форме круга. Изучение круга и его развитие применимо в областях математики, геометрии, астрономии и исчисления.
В терминологии круга используются следующие термины:
дуга: любая связанная часть круга.
Центр: точка на равном расстоянии от точек на окружности.
Радиусотрезок, соединяющий центр круга с любой точкой на самом круге; или длина такого отрезка, равная половине диаметра.
Диаметротрезок, конечные точки которого лежат на окружности и который проходит через центр; или длина такого отрезка, который является наибольшим расстоянием между любыми двумя точками на окружности. Это особый случай аккорда, а именно самого длинного аккорда, и он вдвое больше радиуса.
длина окружностие: длина одной цепи по кругу.
Аккорд: отрезок, конечные точки которого лежат на окружности.
касательный: копланарная прямая, которая касается круга в одной точке.
Semicirclе: область, ограниченная диаметром, и дуга, лежащая между конечными точками диаметра. Это частный случай кругового сегмента, а именно самого большого.
Круговой сектор: область, ограниченная двумя радиусами и дуга, лежащая между радиусами.
Математически эллипс является распространенной формой в области математики. Его определение гласит: изогнутая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна. Реальные примеры эллипса: обруч, стакан воды и простая тарелка для обеда, когда они наклонены, чтобы смотреть под углом.
Аполлоний Пергский дал название «эллипс» в своей конике, которая подчеркивает связь кривой с применением областей. Это кривая на плоскости, которая окружает две точки фокусировки, так что прямая линия, проведенная из одной из точек фокусировки в любую точку кривой, а затем обратно в другую точку фокусировки, имеет одинаковую длину для каждой точки кривой. Его форма представлена его эксцентриситетом, который произвольно близок к 1. Изучение эллипса и его свойств широко применимы в области физики, астрономии и техники. Орбиты планет с Солнцем в одной из фокусных точек, лун, вращающихся вокруг планет, и другие системы, имеющие два астрономических тела, являются общими примерами эллиптических траекторий. Форма планет и звезд часто хорошо описывается эллипсоидами. Эллипс также считается самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения являются синусоидами с одинаковой частотой.
Термины, используемые в основном в терминологии эллипса:
фокус: Расстояние от центра, и выражается в терминах большого и малого радиусов.
эксцентричность: Эксцентриситет эллипса (обычно обозначаемый как e или ε) выражается в терминах с использованием коэффициента уплощения.
директриса: это линия, параллельная малой оси, с которой связан каждый фокус.
Латус прямой кишки: Хорды эллипса, которые перпендикулярны большой оси и проходят через один из ее фокусов, называются широчайшей прямой кишкой эллипса.
Большая / Малая осьСамый длинный и самый короткий диаметры эллипса. Длина большой оси равна сумме двух линий генератора.
Полу мажор / Полу минор оси: Расстояние от центра до самой дальней и ближайшей точки на эллипсе. Половина большой / малой оси.
Аккорды: Середины набора параллельных аккордов эллипса коллинеарны.
Длина окружности: он связан с длиной большой полуоси и эксцентриситетом и является неотъемлемой частью эллипса.
Сравнение между Кругом и Эллипсом:
Круг | Эллипс | |
Определения | Круг — это круглая плоская фигура, граница которой (окружность) состоит из точек, равноудаленных от неподвижной точки (центра). | Эллипс представляет собой правильную овальную форму, отслеживаемую точкой, движущейся в плоскости, так что сумма его расстояний от двух других точек (фокусов) является постоянной, или он получается, когда конус разрезается наклонной плоскостью, что не пересекать базу. |
вариации | Круги не различаются по форме; они остаются той же формы, даже когда вид меняется. | Эллипсы варьируются по форме от очень широких и плоских до почти круглых, в зависимости от того, как далеко расположены фокусы друг от друга. |
Радиус согласованности | Он имеет постоянный радиус по всей форме. | Он не имеет постоянного радиуса по всей форме. |
Основные компоненты |
Овалы и эллипсы — блог Привычка не думать
Добрый день.
А давайте попробуем написать краткие сочинения для нынешних выпускников на тему «Почему стоит выбрать изучение такой-то науки?» Вдруг кто-то сейчас как раз колышется с выбором, в какой вуз или на какой факультет податься, а мы ему ещё сильнее карты спутаем… Ниже предлагаю свою версию про всякую математику и геометрию (ранее была и другая запись на близкую тему — «Зачем изучать математику?») Приглашаю вас поделиться своим вариантом!
Итак, долгое время я считал, что «овал» — это жаргонное название эллипса. Потом начались уроки черчения, на которых нас учили рисовать в том числе и овалы (как четвёрку дуг: две одного радиуса и две — другого). Уже тогда было понятно, что эллипс циркулем и линейкой не нарисовать, поэтому по данному свойству овал казался куда удобнее, хоть и нелепее. А затем и вовсе началась эпоха интернета, поэтому узнать о том, что такое овал может каждый, но уже не каждому это понравится или даже захочется сделать.
Чем же хорошо нам всем знакомый эллипс драматически отличается от множества других хорошо знакомых фигур? Оказывается, мы не можем выразить длину дуги произвольного эллипса в элементарных функциях. Вот для частных случаев ещё справиться можем: например, если эллипс является окружностью, то всё хорошо — длина дуги выражается как удвоенное произведения радиуса и числа Пи. А вот с произвольным эллипсом, задаваемым парой радиусов a и b, такое уже не пройдёт.
Кстати, легко понять, что для частного случая овала с уроков черчения никаких проблем нет: раз он состоит из дуг окружностей, то про него мы всё знаем.
Но всё равно сложно избавиться от ощущения, что что-то здесь не так. Как может простой эллипс, легко получаемый растяжением окружности, вызывать какие-то проблемы, если с самой окружностью всё достаточно легко? Чтобы понять это, давайте сравним периметры и площади у следующих фигур:
Казалось бы, если мы знаем площадь круга радиуса a, то знаем и площадь эллипса эллипса с радиусами a и b (достаточно домножить площадь круга на b/a, чтобы получить искомое значение). Этот же трюк прекрасно работает на квадратах, что совершенно правильно и естественно. В чём же проблема с периметром? Может показаться, что всё должно быть совершенно аналогично. Но мысленный эксперимент с растяжением квадрата эту теорию легко ломает… Иногда полезно попредставлять такие штуки, чтобы лучше чувствовать, чем отличается длина от площади.
К сожалению, описанную выше проблему с невозможностью выразить длину дуги эллипса нередко формулируют неверно (что-то вроде «на дворе 21 век, а математики так и не смогли найти формулу эллипса» или даже грубее; иногда, видимо, желая упростить, журналисты позволяют себе говорить, что число Пи равно трём, поэтому фраза про математиков, которые «до сих пор не могут одолеть эллипс» не слишком раздражает). Как вы понимаете, эллипс человечество знает очень давно и исследовало весьма плотно. Дело не в том, что математики чего-то не смогли, а в том, что это принципиально невозможно.
Казалось бы, обычная сплющенная окружность, а уже вылезают дивные эффекты! Если вас завораживает эта мысль и вы как раз заканчиваете школу, то хорошо подумать о поступлении на математический факультет определённо стоит. Ведь гораздо интереснее учиться тому, что вам нравится (см. об этом ещё тут).
А если вы любите всякое красивое и геометрическое, то рекомендую статью с массой внятных анимированных картинок про арбелос.
Овал, свойства овала
Овал, свойства овала.
Овал ― это плоская замкнутая строго выпуклая гладкая кривая.
Овал (понятие и определение)
Свойства овала
Овал (понятие и определение):
Овал (фр. ovale, от лат. ovum – «яйцо») ― это плоская замкнутая строго выпуклая гладкая кривая. Овал пересекается с любой прямой не более двух раз.
Овал – это замкнутая выпуклая кривая, очерченная дугами окружностей, плавно переходящих друг в друга.
Овал относится к двухмерным фигурам. Овал имеет правильную форму. Внешне овал напоминает форму яйца.

Рис. 1. Овал
Точки овала, в которых кривизна овала достигает экстремума, называются его вершинами.
Овал может иметь одну или две оси симметрии, а может и не иметь оси симметрии.

Рис. 2а. Овал с 2 осями симметрии

Рис. 2б. Овал с 1 осью симметрии

Рис. 2в. Овал, не имеющий осей симметрии
Простейшим примером овала является эллипс (в частности, окружность). В свою очередь эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Для эллипса характерно уравнение: F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const

Рис. 3. Эллипс
Иными словами, овалом обозначают более общее понятие, а эллипс – это особенное понятие.
Свойства овала:
1. Овал пересекается с любой прямой не более двух раз.

Рис. 4. Овал и прямые
2. Овал имеет не менее четырёх вершин.

Рис. 5. Овал
3. Если овал имеет в каждой своей точке определённую касательную, то любому направлению на плоскости соответствуют две и только две касательные, параллельные этому направлению.
Квадрат
Овал
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Развернутый угол
Ромб
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности 168
Овалпротив эллипса — какая разница?
овал
Овал (от латинского ovum, «яйцо») — это замкнутая кривая в плоскости, которая «слабо» напоминает контур яйца. Этот термин не очень специфичен, но в некоторых областях (проективная геометрия, технический чертеж и т. Д.) Ему дается более точное определение, которое может включать одну или две оси симметрии. В обычном английском языке термин используется в более широком смысле: любая форма, которая напоминает яйцо. Трехмерная версия овала называется овоидом.
Эллипс
В математике эллипс — это кривая в плоскости, которая окружает две точки фокусировки, так что сумма расстояний до двух точек фокусировки постоянна для каждой точки кривой. Таким образом, это обобщение круга, представляющего собой особый тип эллипса, в котором обе точки фокусировки находятся в одном и том же месте. Форма эллипса (насколько он «вытянут») представлена его эксцентриситетом, который для эллипса может быть любым числом от 0 (предельный случай круга) до произвольно близкого значения, но меньше 1.
Эллипсы — это закрытый тип конического сечения: плоская кривая, полученная в результате пересечения конуса с плоскостью (см. Рисунок справа). Эллипсы имеют много общего с двумя другими формами конических сечений: параболами и гиперболами, которые являются открытыми и неограниченными. Поперечное сечение цилиндра является эллипсом, если только сечение не параллельно оси цилиндра.
Аналитически эллипс также может быть определен как набор точек, так что отношение расстояния каждой точки на кривой от данной точки (называемой фокусом или фокусной точкой) к расстоянию от этой же точки на кривой для данной линии (называется директриса) является константой.Это соотношение является вышеупомянутым эксцентриситетом эллипса.
Эллипс также может быть определен аналитически как набор точек, для каждой из которых сумма его расстояний до двух фокусов является фиксированным числом.
Эллипсы распространены в физике, астрономии и технике. Например, орбита каждой планеты в нашей солнечной системе является приблизительно эллипсом с барицентром пары планета-Солнце в одной из фокусных точек. То же самое верно для лун, вращающихся вокруг планет и всех других систем, имеющих два астрономических тела.Формы планет и звезд часто хорошо описываются эллипсоидами. Эллипсы также возникают как образы окружности в параллельной проекции и ограниченные случаи перспективной проекции, которые являются просто пересечениями проективного конуса с плоскостью проекции. Это также самая простая фигура Лиссажу, сформированная, когда горизонтальные и вертикальные движения являются синусоидами с одинаковой частотой. Подобный эффект приводит к эллиптической поляризации света в оптике.
Название ἔλλειψις (élleipsis, «упущение») было дано Аполлонием Пергским в его «Конике», подчеркивая связь кривой с «применением областей».
овальные против эллиптических — какая разница?
овал
Овал (от латинского ovum, «яйцо») — это замкнутая кривая в плоскости, которая «слабо» напоминает контур яйца. Этот термин не очень специфичен, но в некоторых областях (проективная геометрия, технический чертеж и т. Д.) Ему дается более точное определение, которое может включать одну или две оси симметрии. В обычном английском языке термин используется в более широком смысле: любая форма, которая напоминает яйцо. Трехмерная версия овала называется овоидом.
Эллиптический
В математике эллипс — это кривая в плоскости, которая окружает две точки фокусировки, так что сумма расстояний до двух точек фокусировки постоянна для каждой точки кривой. Таким образом, это обобщение круга, представляющего собой особый тип эллипса, в котором обе точки фокусировки находятся в одном и том же месте. Форма эллипса (насколько он «вытянут») представлена его эксцентриситетом, который для эллипса может быть любым числом от 0 (предельный случай круга) до произвольно близкого значения, но меньше 1.
Эллипсы — это закрытый тип конического сечения: плоская кривая, полученная в результате пересечения конуса с плоскостью (см. Рисунок справа). Эллипсы имеют много общего с двумя другими формами конических сечений: параболами и гиперболами, которые являются открытыми и неограниченными. Поперечное сечение цилиндра является эллипсом, если только сечение не параллельно оси цилиндра.
Аналитически эллипс также может быть определен как набор точек, так что отношение расстояния каждой точки на кривой от данной точки (называемой фокусом или фокусной точкой) к расстоянию от этой же точки на кривой для данной линии (называется директриса) является константой.Это соотношение называется эксцентриситетом эллипса.
Эллипс также может быть определен аналитически как набор точек, для каждой из которых сумма его расстояний до двух фокусов является фиксированным числом.
Эллипсы распространены в физике, астрономии и технике. Например, орбита каждой планеты в нашей солнечной системе является приблизительно эллипсом с барицентром пары планета-Солнце в одной из фокусных точек. То же самое верно для лун, вращающихся вокруг планет и всех других систем, имеющих два астрономических тела.Формы планет и звезд часто хорошо описываются эллипсоидами. Эллипсы также возникают как образы окружности в параллельной проекции и ограниченные случаи перспективной проекции, которые являются просто пересечениями проективного конуса с плоскостью проекции. Это также самая простая фигура Лиссажу, сформированная, когда горизонтальные и вертикальные движения являются синусоидами с одинаковой частотой. Подобный эффект приводит к эллиптической поляризации света в оптике.
Название ἔλλειψις (élleipsis, «упущение») было дано Аполлонием Пергским в его «Конике», подчеркивая связь кривой с «применением областей».
Очагов эллипса — Math Open Reference
Очаги эллипса — Math Open Reference Две точки внутри эллипса, которые используются в его формальном определении. Смотрите определение эллипса.Попробуйте это Перетащите любую оранжевую точку. Изменяя форму эллипса, обратите внимание на то, как движутся две точки фокусировки (F1 и F2).
Эллипс имеет две точки фокусировки. Слово foci (произносится « foe -sigh») является множественным числом слова «фокус». Один фокус, два очага.
Очаги всегда лежат на большой (самой длинной) оси, расположенной на равных сторонах от центра. Если главная ось и малая ось имеют одинаковую длину, фигура представляет собой круг, и оба очага находятся в центре. Измените форму эллипса выше и попытайтесь создать эту ситуацию.
Обратите внимание, что главная ось всегда самая длинная, поэтому если вы сделаете эллипс узким, это будет вертикальная ось вместо горизонтальной.
Расчет местоположений фокусов
Эллипс частично определяется расположением очагов.Однако, если у вас есть эллипс с известной длиной большой и малой осей, Вы можете найти расположение очагов, используя формулу ниже. Длина главной и малой оси — это ширина и высота эллипса. гдеF — расстояние от каждого фокуса до центра (см. Рисунок выше)
j — большая полуось (большой радиус)
n — полуминорная ось (малый радиус)
На рисунке выше перетащите любую из четырех оранжевых точек.Это изменит длину главной и вспомогательной осей. Ты увидишь как движутся фокусы, и расчет изменится, чтобы отразить их новое местоположение.
Нахождение очагов с компасом и линейкой
Имея эллипс с известной высотой и шириной (большая и малая полуоси), вы можете найти два фокуса, используя компас и линейку.
Основная идея в конструкции показана ниже. Точка R является концом малой оси и находится прямо над центральной точкой O, и так а = б.По определению, a + b всегда равно длине главной оси QP, независимо от того, где R. Таким образом, a + b равно OP + OQ. Так что б должно равняться ОП. (И равно OQ).
Конструкция работает, устанавливая ширину компаса на OP, а затем дважды отмечая дугу от R по главной оси, создавая F1 и F2. Для получения дополнительной информации см.
Оптические свойства
Если внутри эллипса есть зеркало, луч света, покидающий один фокус, всегда будет проходить через другой. Подробнее об этом смотрите Оптические свойства эллиптических зеркал
Другие темы эллипса
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
овал против круга — какая разница?
Круг (существительное)
Двумерная геометрическая фигура, линия, состоящая из набора всех этих точек на плоскости, которые одинаково удалены от заданной точки (центра).
«Множество всех точек (x, y), таких что (x-1) 2 + y 2 »
«=»
«r 2 является окружностью радиуса r вокруг точки (1, 0). »
Круг (существительное)
Двумерная геометрическая фигура, диск, состоящий из набора всех этих точек плоскости на расстоянии, меньшем или равном фиксированному расстоянию (радиусу) от данной точки.
Круг (существительное)
Любой тонкий трехмерный эквивалент геометрических фигур.
«Надень шапку и садись на этот круг».
Круг (существительное)
Кривая, которая более или менее образует часть или весь круг.
«двигаться по кругу»
Круг (существительное)
Орбита.
Круг (существительное)
Определенная группа лиц; особенно тот, кто разделяет общий интерес.
«Внутренний круг»;
«круг друзей»
Круг (существительное)
Линия, состоящая из двух полукругов радиусом 30 ярдов, центрированных на калитках, соединенных прямыми линиями, параллельными полю, используемому для обеспечения ограничений поля в однодневном матче.
Круг (существительное)
Ритуальный круг, который трижды разыгрывается на обличье и трижды закрывает вандершинов в воздухе с помощью палочки или буквально с камнями или другими предметами, используемыми для поклонения.
Круг (существительное)
Транспортная развязка или кольцевая развязка.
Circle (существительное)
Compass; цепи; корпус.
Круг (существительное)
Инструмент наблюдения, градуированная конечность которого состоит из целого круга. Когда прикреплено к стене в обсерватории, это называется кругом настенной росписи; при установке с телескопом по оси и по оси Y, в плоскости меридиана, меридиана или транзитного круга; при включении принципа отражения, подобно секстанту, отражающий круг; и когда это повторение угла несколько раз непрерывно вдоль градуированной конечности, повторяющийся круг.
Круг (существительное)
Ряд, заканчивающийся в том месте, где он начинается, и повторяющийся.
Круг (существительное)
Форма аргумента, в которой два или более недоказанных утверждения используются для доказательства друг друга; неокончательные рассуждения.
Круг (существительное)
Косвенная форма слов; волокита.
Круг (существительное)
Территориальное деление или район.
«Десять кругов Священной Римской империи были теми княжествами или провинциями, которые имели места в немецком сейме.»
Circle (существительное)
Мешковина кожи под глазами из-за недосыпания.
» » После работы всю ночь у нее были круги под глазами. «
Circle (глагол)
Чтобы путешествовать по изогнутой траектории.
Круг (глагол)
Вокруг.
Круг (глагол)
Чтобы поместить или отметить круг вокруг.
«Обведите кружком задания, которыми вы являетесь заинтересован в подаче заявки на.»
Круг (глагол)
Для кругов.
» Стервятники кружили над головой «.