Гипотезы пуанкаре доказательство – Теорема Пуанкаре – математическая формула «Вселенной». Григорий Перельман. Часть 1 (из серии «Настоящий Человек в науке»)
Гл. 3 Гипотеза Пуанкаре. Григорий Перельман и гипотеза Пуанкаре
Гл. 3 Гипотеза Пуанкаре
«Математика — не просто создание человеческого разума, она испытывает на себе сильное влияние тех культур, в рамках которых развивается. Математические «истины» зависят от людей ничуть не меньше, чем восприятие цвета или язык».
Людвиг Виттенштейн
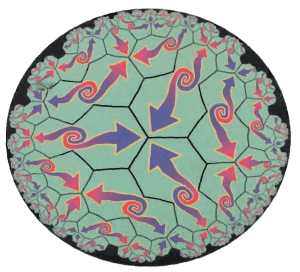
Рис. 18. Топологическое многообразие Пуанкаре
Всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере.
«С того момента, как гипотеза Пуанкаре была сформулирована более ста лет назад, сообщения о ее доказательстве появлялись почти ежегодно. Анри Пуанкаре, двоюродный брат Раймонда
-47-
Пуанкаре, президента Франции во время Первой мировой войны, был также одним из талантливейших математиков девятнадцатого века. Худой, близорукий, известный своей невероятной рассеянностью, Пуанкаре сформулировал знаменитую задачу за восемь лет до своей смерти, в 1904 году. Формулировка проблемы в качестве побочного вопроса была засунута в конец шестидесятипятистраничной статьи.
Пуанкаре не смог добиться сколько-нибудь заметного прогресса в решении этой проблемы. «Cette question nous entrainerait trop loin» («Этот вопрос уводит нас далеко в сторону»), — писал он. Пуанкаре был основателем топологии — науки, также называемой «геометрией резинового листа» из-за ее ориентации на исследование внутренних свойств различных пространств».
Сильвия Насер, Дэвид Грубер. Многообразная судьба. Легендарная проблема и битва вокруг ее решения
Страсть великого французского ученого к построению фундаментальных основ математической науки и его релятивизм, отраженный в зеркале собственного философского учения — конвенционализма, привели в итоге к довольно необычной гипотезе строения Мира. В истории науки эту абстрактную математическую проблему, приводящую к важнейшим космологическим выводам, так часто и называют — топологическая гипотеза (теорема, задача, проблема) Пуанкаре.
С помощью молодого математика и непременного члена клуба знатоков «Что? Где? Когда?» Сергея Игоревича Николенко вспомним, что все началось с исследований, которые Пуанкаре вел в области алгебраической геометрии. Он работал над одним из краеугольных камней этой науки — теорией гомологии, особого класса топологических инвариантов. В 1900 году он опубликовал статью, в которой доказывал, что если у трехмерной поверхности гомология совпадает с гомологией сферы, то и сама поверхность — сфера; на самом деле это утверждение даже более сильное, чем утверждение гипотезы Пуанкаре.
Однако в его рассуждения вкралась ошибка, которую он сам и нашел, к 1904 году разработав важнейшее понятие фундаментальной группы и построив на его базе контрпример
-48-
к собственной теореме. Тогда же он наконец поставил вопрос правильно.
Достаточно долго на гипотезу не обращали внимания. Интерес к ней пробудил Джон Генри Константин Уайтхед (1904–1960) — выдающийся английский математик, один из основателей теории гомотопий. Не следует путать его с дядей Альфредом Уайтхедом, тоже математиком, но специализировавшемся на логике и алгебре, написавшем вместе с Бертраном Расселом знаменитую монографию «Принципы математики», который в 30-е годы прошлого века объявил о том, что нашел-таки доказательство теоремы Пуанкаре. К сожалению, представленные расчеты в итоге оказались неверны, однако в процессе поиска и попыток исправить свои неточности он обнаружил интереснейшие классы трехмерных поверхностей и значительно продвинул теорию, которая позднее получила название топологии малых (или низших) размерностей. В 1950-1960-е годы всплеск интереса к проблеме вновь породил несколько ошибочных заявлений о том, что теорему удалось доказать, но после всесторонних проверок математики наконец поняли, что гипотеза Пуанкаре при своей внешней простоте, подобно знаменитой теореме Ферма, содержит множество подводных камней.
К тому времени топология низших размерностей стала отдельной ветвью математики и аналоги задачи Пуанкаре были доказаны для более высоких размерностей. Этому послужила удивительная причина: оказалось, что в невообразимом мире многих измерений эта часть геометрии устроена гораздо проще! Тем временем привычный нам «Трехмерный случай» продолжал оставаться камнем преткновения.
Гипотеза Пуанкаре является одной из наиболее известных задач топологии. Она дает достаточное условие того, что пространство является трехмерной сферой с точностью до деформации.
В гипотезе Пуанкаре утверждает, что:
«Всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере».
Гипотеза Пуанкаре — одна из тех задач, в которых даже ошибочные решения приводят к появлению новых областей
-49-
математики; в этом с ней может соперничать разве что великая теорема Ферма. Кроме общедоступности формулировки у задачи Пуанкаре есть еще и внешние параллели с теоремой Ферма. Обе математические проблемы были сформулированы великими математиками вне сферы их основных интересов и были решены гениальными одиночками после многолетнего глубокого погружения в задачу.
Многочисленные книги по занимательной математике, мимо которых мало кто прошел в детстве, любят рассказывать о топологии — странной науке, в которой два предмета сравниваются только по количеству дырок в них: чайная чашка ничем не отличается от бублика, а апельсин — от Солнца. На самом деле топология — очень глубокая наука и объекты и свойства, которые она изучает, весьма многочисленны и разнообразны. Прежде чем выяснить, в чем состоит гипотеза Пуанкаре, необходимо разобраться именно в топологии, к которой эта гипотеза и относится.
Топология многообразий занимается свойствами поверхностей, которые не меняются при определенных деформациях. Приведем классический пример. Предположим, что на столе лежит бублик и стоит пустая чашка. С точки зрения геометрии и здравого смысла это разные объекты хотя бы потому, что выпить кофе из бублика не получится при всем желании.
Рис. 19. Гипотеза Перельмана для топологии низших измерений
Если представить себе ячейку высокоразмерного континуума и постепенно избавляться от «лишних» изменений,
-50-
то на определенном этапе «уплощенное» пространство начнет автомодельным образом «само по себе» сворачиваться в идеальную сферу.
Гипотеза, сформулированная французским математиком Анри Пуанкаре в 1904 году, является центральной проблемой топологии, науки о геометрических свойствах тел, которые не меняются, когда тело вытягивается, скручивается или сжимается. Топологически двухмерную сферу можно сравнительно легко представить как планетарную поверхность, например лунную или земную. Но трехмерный шар в четырехмерном пространстве вообразить уже довольно сложно. Между тем Пуанкаре утверждал, что трехмерная сфера — это единственное ограниченное трехмерное пространство без дыр. Предположение о подобных свойствах многомерного пространства он сделал в 1904 году, когда только начинал заниматься топологией.
Однако тополог скажет, что чашка и бублик — это одно и то же. И объяснит это так. Вообразите, что чашка и бублик представляют собой поверхности, полые внутри и изготовленные из очень эластичного материала (математик бы сказал, что имеется пара компактных двумерных многообразий). Проведем умозрительный эксперимент: сначала раздуем дно чашки, а потом ее ручку, после чего она превратится в тор (именно так математически называется форма бублика).
Разумеется, у пытливого читателя возникает вопрос: раз поверхности можно мять, то как же их различать? Ведь интуитивно понятно: как ни мни тор, без разрывов и склеек сферу из него не получишь. Тут в игру вступают так называемые инварианты — характеристики поверхности, которые не меняются при деформации, — понятие, необходимое для формулировки гипотезы Пуанкаре.
Здравый смысл подсказывает, что тор от сферы отличает дырка. Однако дырка — понятие далеко не математическое, поэтому его надо формализовать. Делается это так: представим, что на поверхности имеется очень тонкая эластичная нить, образующая петлю (саму поверхность в этом умозрительном опыте, в отличие от предыдущего, считаем твердой).
-51-
Будем двигать петлю, не отрывая ее от поверхности и не разрывая. Если нить можно стянуть до очень маленького кружочка (почти точки), то говорят, что петля стягиваема. В противном случае петля называется нестягиваемой.
Можно легко увидеть, что на сфере любая петля стягиваема, а вот для тора это уже не так: на бублике есть целых две петли — одна продета в дырку, а другая обходит дырку по периметру, которые нельзя стянуть. На рис. 19 показаны примеры нестягиваемых петель. Когда на поверхности есть петли, математики говорят, что «фундаментальная группа многообразия нетривиальна», а если таких петель нет — то тривиальна.
Теперь, чтобы правильно сформулировать гипотезу Пуанкаре, осталось потерпеть еще немного: надо разобраться, что такое трехмерное многообразие в общем и трехмерная сфера в частности.
Вернемся на секунду к поверхностям, которые мы обсуждали выше. Любую из них можно разрезать на очень мелкие кусочки, каждый из которых будет напоминать кусочек плоскости. Так как у плоскости всего два измерения, то говорят, что и многообразие двумерно. Трехмерное многообразие — это такая поверхность, которую можно разрезать на мелкие кусочки, каждый из которых очень похож на кусочек обычного трехмерного пространства.
Главным «действующим лицом» гипотезы является трехмерная сфера. Представить себе трехмерную сферу как аналог обычной сферы в четырехмерном пространстве, не потеряв при этом рассудок, все-таки, наверное, невозможно. Однако описать этот объект, так сказать, «по частям» достаточно легко. Все, кто видел глобус, знают, что обычную сферу можно склеить из северного и южного полушарий по экватору. Так вот, трехмерная сфера склеивается из двух шаров (северного и южного) по сфере, которая представляет собой аналог экватора.
На трехмерных многообразиях можно рассмотреть такие же петли, какие мы брали на обычных поверхностях. Так вот, гипотеза Пуанкаре утверждает: «Если фундамен-
-52-
тальная группа трехмерного многообразия тривиальна, то оно гомеоморфно сфере». Непонятное словосочетание «гомеоморфно сфере» в переводе на неформальный язык означает, что поверхность может быть преобразована в сферу.
Будем чуточку более формальны. Говорят, что поверхность k-связна, если на ней можно провести k-1 замкнутую кривую, которая не делит ее на две части. Сфера (поверхность апельсина) односвязная: как ни проводи на ней замкнутую кривую, кусочек вырежется; а вот поверхность бублика двусвязная — ее можно, например, разрезать поперек, превратив в цилиндр, но сохранив целостность (а вот повторно разрезать цилиндр уже не получится). Для поверхностей в трехмерном пространстве это свойство как раз и означает, что в поверхности есть
Другое важное понятие — гомеоморфизм — также уже встречалось в рассуждениях о неразличимости чашки и бублика. Именно в этой неразличимости и дело: гомеоморфизм — это непрерывное преобразование, деформация, которой можно подвергнуть множество, сохранив при этом его топологические свойства (например, k-связность). Чашку легко непрерывным преобразованием превратить в бублик, а апельсин — в Солнце. При этом преобразовании сохраняются важнейшие топологические инварианты, такие как число k. Два множества, которые можно гомеоморфизмом превратить друг в друга, с топологической точки зрения считаются эквивалентными.
Гипотеза Пуанкаре состоит в том, что каждая односвязная трехмерная поверхность гомеоморфна трехмерной сфере. Обратите особое внимание на то, что «трехмерная поверхность» может размещаться в пространстве, чья размерность как минимум 4! Трехмерная сфера — это поверхность четырехмерного шара (привычная нам двухмерная сфера — поверхность трехмерного шара).
-53-
Рис. 20. Дискретный код трехмерной поверхности Терстона
Изображенные так называемые ячейки Терстона образуют своеобразную геометрическую головоломку. Если выбрать определенные коды Терстона: 6-8-7, 1-17-9 или 3-20-21, то каждый из них будет подсказывать, в какую геометрическую фигуру сложится трехмерная поверхность.
«В конце семидесятых принстонский математик Уильям Терстон, любивший иллюстрировать свои идеи с помощью ножниц и бумаги, предложил систематизировать все трехмерные многообразия. Он утверждал, что, несмотря на то что многообразия могут принимать любую форму, в действительности они тяготеют к некоторой «предпочтительной» геометрии (подобно тому, как кусок шелка, обернутый вокруг манекена, стремится принять его форму). Терстон предположил, что любое трехмерное многообразие может быть разложено на один или несколько компонентов, каждый из которых можно отнести к одному из восьми типов, включая сферический».
Сильвия Насер, Дэвид Грубер. Многообразная судьба. Легендарная проблема и битва вокруг ее решения
-54-
Доказывать гипотезу Пуанкаре начинают с произвольной римановой метрики на односвязном трехмерном многообразии М и применяют к нему поток Риччи с хирургией. Важным шагом является доказательство того, что в результате такого процесса «выбрасывается» все. Это означает, что исходное многообразие М можно представить как набор сферических пространственных форм, соединенных друг с другом трубками. Подсчет фундаментальной группы показывает, что М диффеоморфно связанной сумме набора пространственных форм. Таким образом, М является связной суммой набора сфер, то есть сферой.
К теме гипотезы Пуанкаре примыкает важная для кибернетиков область математики — вычислительная топология. Вычислительные и распознавательные задачи, оказывается, есть и в этой абстрактной науке. С одной из таких задач связана предпринятая в 1974 году очень интересная попытка решения проблемы Пуанкаре в ее алгоритмической версии.
Каждая трехмерная поверхность задается некоторым (не будем вдаваться в подробности) дискретным кодом — конечным набором символов. Одна и та же поверхность имеет бесконечное число различных кодировок. Естественный вопрос: существует ли алгоритм, определяющийся по заданному кодовому слову, задает ли это слово трехмерную сферу в новой алгоритмической проблеме Пуанкаре? Именно эту задачу исследовал ряд видных российских математиков в 1974 году, предположив, что определенное свойство кода (оно было названо «волной») дает критерий «сферичности». Однако им удалось только доказать, что наличие «волны» гарантирует: перед нами сфера. Доказать же, что в любом коде, задающем сферу, имеется «волна», никак не получалось. Тогда авторы сделали весьма оригинальный по тем временам ход: провели масштабный компьютерный эксперимент. Была написана программа для машины БЭСМ-6, которая случайным образом генерировала коды, задающие трехмерную сферу, и проверяла наличие в них «волны». В эксперименте, потребовавшем весьма длительного счета, был проверен миллион таких случайных
-55-
представлений сферы — и во всех обнаружилась «волна»! Это был довольно веский аргумент в пользу корректности предложенного алгоритма. Но авторы, будучи серьезными математиками воздерживались от поспешных заявлений. И не напрасно: спустя пару лет был обнаружен контрпример…
Спустя 20 лет алгоритм распознавания 3-сферы (за экспоненциальное время) был все же построен. Однако общая проблема алгоритмического распознавания поверхностей размерности-3 открыта, она активно изучается и сегодня, в то время как для более высоких размерностей давно известна ее неразрешимость, а для размерности-2 она была решена еще раньше.
По мнению современного философа А. В. Дахина, особенно важно отметить, что теорема Пуанкаре — Перельмана содержит идею о возможности существования в глобальной Вселенной двух структур пространства.
Профессор Дахин считает, что имеет смысл обратиться к следующим закономерным вопросам: почему может существовать пространство с дыркой и почему может существовать пространство без дырки? Как существует пространство с дыркой и как существует пространство без дырки? И более глубокий вопрос: что находится внутри дырки и где это «что-то», когда дырка отсутствует?
Эти вопросы можно проиллюстрировать в терминах проблемы начала Вселенной. Резонно предложить две картины: одна из них показывает, что начало — это точечный объект (материальная частица), а другая картина будет отражать, что начало Вселенной — это не материя, а дырка (ничто или дух), где время и пространство отсутствуют.
«Теория Терстпона, получившая название гипотезы геометризации, описывает все возможные трехмерные многообразия и, таким образом, является очень важным обобщением гипотезы Пуанкаре. Доказательство гипотезы Терстона влекло за собой доказательство проблемы Пуанкаре. Доказательство теорий Терстона и Пуанкаре «открывало огромные перспективы», как признал Барри Мазур, математик из Гарвардского
-56-
университета. Последствия этих доказательств для других областей науки могут быть неочевидны еще долгое время, но, без сомнения, для математиков эти задачи имели фундаментальное значение. «Эти задачи — что-то вроде теоремы Пифагора XX века, — добавил Мазур. — Они оказывают огромное влияние на математику»».
Сильвия Насер, Дэвид Грубер. Многообразная судьба. Легендарная проблема и битва вокруг ее решения
Диалектический подход призывает к тому, чтобы найти концепт, обобщающий обе модели пространства. Базовая идея здесь была выдвинута именно Пуанкаре, который обосновал различие (и взаимосвязанность) между картезианской моделью пространства (трехмерная система) и моделью «живого» пространства, представленной в работах самого Пуанкаре (сферическая система). В частности, он дал собственное определение термина «точка пространства» для «живой» пространственной системы. Он показал точку пространства в качестве агента взаимодействий с другими предметами вокруг нее. Соответственно, как агент взаимодействий всякая точка пространства является одновременно и точкой времени, а потому должна быть оснащена собственной памятью.
Итак, было бы разумно заключить: точка пространства-времени — поскольку она является агентом собственных взаимодействий — действует под влиянием собственной памяти и поэтому считается «центром индетерминации» Вселенной. В то же время эта память — своеобразное проявление предшествующей истории агента, которая отсутствует для всех взаимодействий настоящего. Следовательно, память дает всякому агенту некоторую независимость от предметов и взаимодействий настоящего. Рассматривая ситуацию, мы можем заметить, что кроме причин и взаимодействий настоящего агент имеет и некоторые иные источники собственной активности. Иными словами, он имеет собственные источники активности, которые со стороны выглядят как дырки.
-57-
Обобщая сказанное, предположим, что точка пространства-времени имеет два онтологических измерения собственной активности.
• Одно измерение (сфера бытия) связано с влиянием его предшествующей истории; это измерение памяти, которое проявляется как дырка и является невидимой оснасткой активности «центра индетерминации».
• Второе измерение (сфера существования) связано с его взаимодействиями в настоящем; это измерение взаимодействий, и оно проявляется через активность материальных частиц, которые являются видимой оснасткой любой активности центра детерминации.
Рис. 21. Модельные переходы в центр индетерминации Вселенной Пуанкаре
Таким образом, в свете бытийного измерения пространство Вселенной будет проявляться как содержащее дырки, потому что любой предмет или фактор будут повернуты стороной своей памяти. В аспекте существования пространство Вселенной будет проявляться как содержащее материальные частицы, потому что любой предмет или фактор будут высвечены со стороны взаимодействий. В русле диалектики особенно важно подчеркнуть различие и взаимосвязь между обоими измерениями. В заключение своих логических построений профессор Дахин резюмирует, что теория глобаль-
-58-
ной эволюции Вселенной не может быть адекватной, если она будет по-прежнему оснащена только одним концептуальным измерением.
Итак, перед нами абстрактная геометрическая или, точнее, топологическая проблема, которая определенно сильно повлияла на умонастроения великого французского метафизика (так со времен Аристотеля называют ученых, занимающихся философией науки). Это было какое-то особое влияние, заставившее Пуанкаре связать в один тугой узел логических построений конвенционализм, релятивизм и топологию иных измерений. Что предстало перед изумленным взором ученого, когда ему удалось распутать эту научную проблему?
Это было какое-то новое миропонимание, настолько необычное, что оно и стало причиной знаменитого «молчания Пуанкаре»…
Однако проблема Пуанкаре при всей своей загадочности предполагала еще и решение, и оно тоже открывало нечто принципиально новое в облике нашего Мира…
Моррис Клайн в свое время писал, что, хотя математика и является чисто человеческим творением, она открыла доступ к некоторым тайнам природы и этим позволила добиться успехов, превзошедших все ожидания. Как это ни парадоксально, но именно столь далекие от реальности математические абстракции дали человеку возможность многого достичь. Сколь ни искусственно, а иногда и сказочно математическое описание, в нем есть своя мораль. Для мыслящего ученого математическое описание всегда было неиссякаемым источником удивления, рожденного тем, что природа проявляет столь высокую степень соответствия математическим формулам. Заложены ли регулярные зависимости, выражаемые физическими законами, в самой природе и мы лишь открываем их или их изобретает и применяет к природе разум ученого — в любом случае ученые должны надеяться, что их неустанный труд способствует более глубокому проникновению в тайны природы.
-59-
Именно здесь сходятся первые три пазла нашей исторической физико-математической головоломки: физический релятивизм, алгебраическая топология и философия конвенционализма. Все вместе это должно было вызвать какой-то прорыв в миросозерцании ученого. Прорыв настолько впечатляющий и открывающий такие горизонты познания, что Пуанкаре надолго погрузился в глубокое молчание, обдумывая новые перспективы постижения окружающей реальности.
-60-
Поделитесь на страничкеСледующая глава >
biography.wikireading.ru
Что такое гипотеза Пуанкаре простыми словами?
Гипотеза Пуанкаре — это доказанная математическая гипотеза, которая утверждает, что всякое замкнутое n-мерное многообразие гомотопически эквивалентно n-мерной сфере только тогда, когда оно гомеоморфно ей. Попробуем разобрать, что такое гипотеза Пуанкаре простыми словами.
Стоит отметить, сфера (т.е. поверхность шара) является двумерной, а шар — трехмерным.
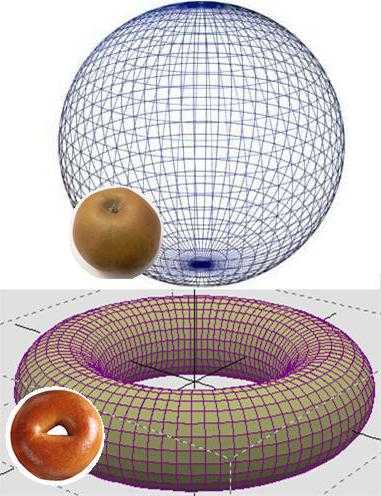
Двумерная сфера включает в себя все точки трехмерного пространства, равноудаленные от некоторой точки, которую называют центром, однако она не принадлежит сфере. Трехмерная же сфера содержит в себе все точки четырехмерного пространства, также равноудаленные от центра, который сфере не принадлежит.
К примеру, воздушный шар легко и без разрывов деформируется в разные фигуры, однако, чтобы сделать из него бублик, нужно будет разрезать шар.
И наоборот, из бублика ну никак не получить цельную сферу. Однако, любая поверхность без разрывов гомеоморфна и может, деформируясь, переходить в шар (сферу). Мы можем опоясать шарик нитью, тогда нить завяжется в 1 узел (с бубликом такое невозможно). Таким образом, сфера (шар) – простейшая трехмерная модель, ее можно свернуть в точку, а также развернуть из точки обратно.
Интересно знать, что с двумерной сферой все было решено еще в XIX веке, а многомерные случаи были доказаны в 1980-х годах. Только трехмерность не была доказана. В 2002-2003 годах Григорий Перельман применил к трехмерным поверхностям уравнение «плавной эволюции» и таким образом сумел показать, что трехмерная поверхность (без разрывов) обязательно будет эволюционировать в трехмерную сферу. По словам ряда специалистов, это была идея «нового поколения», решение которой открывает новые горизонты для математической науки.
otvetikovich.ru
теорема пуанкаре
Гипотеза Пуанкаре
Гипотеза Пуанкаре́ (точнее Теорема Пуанкаре́ — поскольку это доказанная гипотеза) является одной из наиболее известных задач топологии. Она даёт достаточное условие того, что пространство является трёхмерной сферой с точностью до деформации.
Формулировка
Гипотеза Пуанкаре
В исходной форме гипотеза Пуанкаре утверждает. Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере.
Обобщённая гипотеза Пуанкаре.
Обобщённая гипотеза Пуанкаре утверждает: Для любого натурального числа n всякое многообразие размерности n гомотопически эквивалентно сфере размерности n тогда и только тогда, когда оно гомеоморфно ей. Исходная гипотеза Пуанкаре является частным случаем обобщённой гипотезы при n = 3.
История
В 1900 году Пуанкаре сделал предположение, что трёхмерное многообразие со всеми группами гомологий как у сферы гомеоморфно сфере. В 1904 году он же нашёл контрпример, называемый теперь сферой Пуанкаре, и сформулировал окончательный вариант своей гипотезы. Попытки доказать гипотезу Пуанкаре привели к многочисленным продвижениям в топологии многообразий.
Гипотеза Пуанкаре долгое время не привлекала интереса. В 1930-х годах Джон Уайтхед возродил интерес к гипотезе объявив о доказательстве, но затем отказался от него.
Доказательства обобщённой гипотезы Пуанкаре для n ≥ 5 получены в начале 1960—1970-х почти одновременно Смейлом, независимо и другими методами Столлингсом (англ.) (для n ≥ 7, его доказательство было распространено на случаи n = 5 и 6 Зееманом (англ.)). Доказательство значительно более трудного случая n = 4 было получено только в 1982 году Фридманом. Из теоремы Новикова о топологической инвариантности характеристических классов Понтрягина следует, что существуют гомотопически эквивалентные, но не гомеоморфные многообразия в высоких размерностях.
Доказательство исходной гипотезы Пуанкаре (и более общей гипотезы Тёрстона) было найдено только в 2002 году Григорием Перельманом. Впоследствии доказательство Перельмана было проверено и представлено в развёрнутом виде как минимум тремя группами учёных.[1] Доказательство использует модификацию потока Риччи (так называемый поток Риччи с хирургией) и во многом следует плану, намеченному Гамильтоном, который также первым применил поток Риччи.
Схема доказательства
Поток Риччи — это определённое уравнение в частных производных, похожее на уравнение теплопроводности. Он позволяет деформировать риманову метрику на многообразии, но в процессе деформации возможно образование «сингулярностей» — точек, в которых кривизна стремится к бесконечности, и деформацию невозможно продолжить. Основной шаг в доказательстве состоит в классификации таких сингулярностей в трёхмерном ориентированном случае. При подходе к сингулярности поток останавливают и производят «хирургию» — выбрасывают малую связную компоненту или вырезают «шею» (то есть, открытую областьдиффеоморфную прямому произведению ), а полученные две дырки заклеивают двумя шарами так, что метрика полученного многообразия становится достаточно гладкой — после чего продолжают деформацию вдоль потока Риччи.
Процесс, описанный выше, называется «поток Риччи с хирургией». Классификация сингулярностей позволяет заключить, что каждый «выброшенный кусок» диффеоморфен сферической пространственной форме.
При доказательстве гипотезы Пуанкаре начинают с произвольной римановой метрики на односвязном трёхмерном многообразии и применяют к нему поток Риччи с хирургией. Важным шагом является доказательство того, что в результате такого процесса «выбрасывается» всё. Это означает, что исходное многообразие можно представить как набор сферических пространственных форм , соединённых друг с другом трубками . Подсчёт фундаментальной группы показывает, что диффеоморфно связной сумме набора пространственных форм и более того все тривиальны. Таким образом, является связной суммой набора сфер, то есть сферой.
studfiles.net
Проблема Пуанкаре 3
Гипотеза Пуанкаре выдвинута еще в начале XX в. французским математиком Анри Пуанкаре. Чтобы сформулировать ее, дадим
Определение.
Топологическое пространство X называется односвязным, если оно линейно
связно и всякое непрерывное отображение 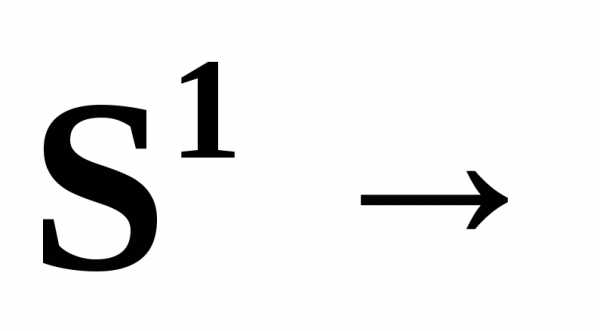 X окружности в пространство X можно продолжить до непрерывного
отображения
X окружности в пространство X можно продолжить до непрерывного
отображения 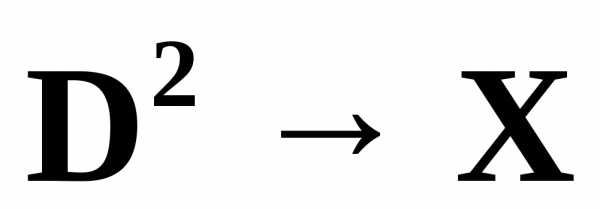 всего круга
всего круга 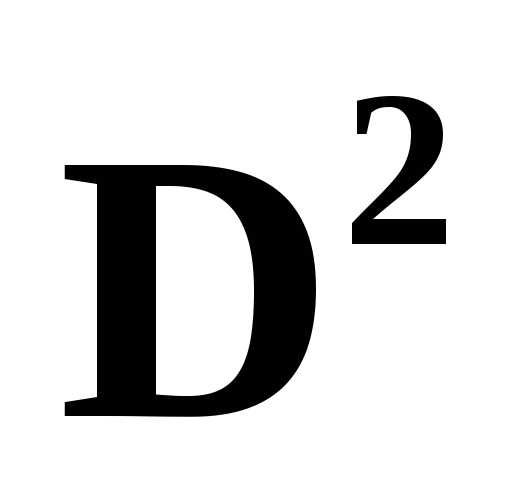 .
Не трудно видеть, что сфера
.
Не трудно видеть, что сфера 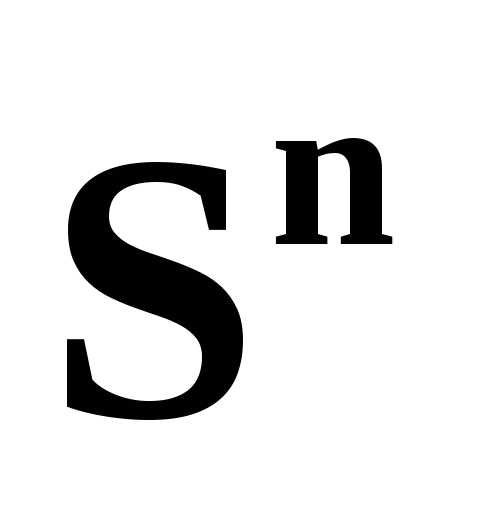 односвязна
при n
односвязна
при n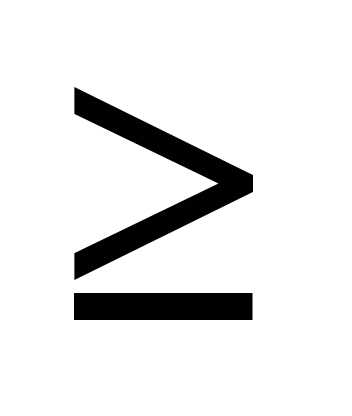 2.
2.
Гипотеза Пуанкаре. Всякое замкнутое односвязное трехмерное многообразие гомеоморфно трехмерной сфере.
Аналоги гипотезы Пуанкаре, касающиеся многообразий размерности 4 и больше, доказаны. Более того, получена топологическая классификация вообще всех замкнутых односвязных четырехмерных многообразий.
Это интересно: Почти 100 лет назад Пуанкаре установил, что двумерная сфера односвязна, и предположил, что трехмерная сфера тоже односвязна.
Другими словами, гипотеза Пуанкаре утверждает, что всякое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере. Гипотеза сформулирована Пуанкаре в 1904 г. Обобщенная гипотеза Пуанкаре утверждает, что для любого n всякое многообразие размерности n гомотопически эквивалентно сфере размерности n тогда и только тогда, когда оно гомеоморфно ей. Для пояснения используют такую картинку: если обмотать яблоко резиновой лентой, то в принципе, стягивая ленту, можно сжать яблоко в точку. Если же обмотать такой же лентой пончик (пирожок с дыркой в середине), то в точку его сжать нельзя без разрыва или пончика, или резины. В таком контексте яблоко называют «односвязной» фигурой, пончик же не односвязен.
Жюль Анри Пуанкаре открыл специальную теорию относительности одновременно с Эйнштейном (1905 г.) и признан одним из величайших математиков за всю историю человечества.
Гипотеза Пуанкаре оставалась недоказанной на протяжении всего двадцатого столетия. В математическом мире она приобрела статус, аналогичный статусу Великой теоремы Ферма.
За доказательство гипотезы Пуанкаре Математический институт им. Клея присудил премию в миллион долларов, что может показаться удивительным: ведь речь идет об очень частном, малоинтересном факте. На самом деле, для математиков важны не столько свойства трехмерной поверхности, сколько факт трудности самого доказательства. В этой задаче в концентрированном виде сформулировано то, что не удавалось доказать с помощью имевшихся ранее идей и методов геометрии и топологии. Она позволяет как бы заглянуть на уровень глубже, в тот пласт задач, который можно будет решить только с помощью идей «нового поколения». Как и в ситуации с теоремой Ферма, выяснилось, что гипотеза Пуанкаре есть частный случай гораздо более общего утверждения о геометрических свойствах произвольных трехмерных поверхностей – гипотезы геометризации Тёрстона (Thurston’s Geometrization Conjecture). Поэтому усилия математиков были направлены не на решение этого частного случая, а на построение нового математического подхода, который способен справляться с такими задачами.
Российский математик Григорий Перельман, сотрудник лаборатории геометрии и топологии Санкт-Петербургского отделения Математического института им. В.А. Стеклова, утверждает, что доказал гипотезу Пуанкаре, то есть решил одну из самых знаменитых нерешенных математических задач. Необычным был способ, который Перельман избрал для обнародования своего доказательства. Вместо того чтобы опубликовать его в солидном научном журнале, что, кстати, было обязательным условием для присуждения приза в миллион долларов, Перельман разместил свою работу на одном из архивов Интернета. Хотя доказательство заняло всего 61 страницу, оно произвело сенсацию в научном мире.
Научный мир рукоплескал гению, обещая золотые горы и почетные титулы. Американский Институт математики Клея был готов присудить ему награду в $1 миллион. Никто не сомневался, что Всемирный конгресс математиков, назовет Перельмана победителем. Кстати, как известно, математики не входят в число учёных, награждаемых Нобелевской премией. Злые языки утверждают, что этот факт не случаен. Ведь, по слухам, именно математик попал в немилость знаменитому шведу Альфреду Нобелю, отбив у него любимую девушку в юности. Между тем российский гений отказался от миллиона, так и не опубликовав свое открытие в специализированных изданиях, уволился из Математического института им. Стеклова РАН, ушел в затворничество и, на церемонии вручения награды, которую вручал король Испании Хуан Карлос I, не появился. Он никак не отреагировал на сообщение о награде и приглашение ее получить, а как говорят знакомые: гений «ушел в леса» по грибы под Санкт-Петербургом.
[http://www.znayki.com/forum/index.php?topic=34.0]
Ученые считают, что 38-летний российский математик Григорий Перельман предложил верное решение проблемы Пуанкаре. Об этом на научном фестивале в Эксетере (Великобритания) заявил профессор математики Стэнфордского университета Кит Девлин.
Проблема (ее также называют задачей или гипотезой) Пуанкаре относится к числу семи важнейших математических проблем, за решение каждой из которых Математический институт Клэя (Clay Mathematics Institute) назначил премию в один миллион долларов. Именно это и привлекло столь широкое внимание к результатам, полученным Григорием Перельманом, сотрудником лаборатории математической физики Санкт-Петербургского отделения Математического института имени Стеклова .
Ученые всего мира узнали о достижениях Перельмана из двух препринтов (статей, предваряющих полноценную научную публикацию), размещенных автором в ноябре 2002-го и марте 2003 года на сайте архива предварительных работ Лос-Аламосской научной лаборатории.
Согласно правилам, принятым Научным консультативным советом института Клэя, новая гипотеза должна быть опубликована в специализированном журнале, имеющем «международную репутацию». Кроме того, по правилам Института, решение о выплате приза принимает, в конечном счёте, «математическое сообщество»: доказательство не должно быть опровергнуто в течение двух лет после публикации. Проверкой каждого доказательства занимаются математики в разных странах мира.
Проблема Пуанкаре
Проблема Пуанкаре относится к области так называемой топологии многообразий — особым образом устроенных пространств, имеющих разную размерность. Двухмерные многообразия можно наглядно представить себе, например, на примере поверхности трехмерных тел − сферы (поверхности шара) или тора (поверхности бублика).
Легко вообразить, что произойдет с воздушным шариком, если его деформировать (изгибать, скручивать, тянуть, сжимать, пережимать, сдувать или надувать). Ясно, что при всех вышеперечисленных деформациях шарик будет изменять свою форму в широких пределах. Однако мы никогда не сможем превратить шарик в бублик (или наоборот) без нарушения непрерывности его поверхности, то есть не разрывая. В этом случае топологи говорят, что сфера (шарик) негомеоморфна тору (бублику). Это означает, что данные поверхности невозможно отобразить одну на другую. Говоря простым языком, сфера и тор различны по своим топологическим свойствам. А поверхность воздушного шарика при всевозможных его деформациях гомеоморфна сфере, равно как поверхность спасательного круга — тору. Иными словами, любая замкнутая двумерная поверхность, не имеющая сквозных отверстий, обладает теми же топологическими свойствами, что и двухмерная сфера.
Проблема Пуанкаре утверждает то же самое для трехмерных многообразий (для двухмерных многообразий, таких как сфера, это положение было доказано еще в XIX веке). Как заметил французский математик, одно из важнейших свойств двухмерной сферы состоит в том, что любая замкнутая петля (например, лассо), лежащая на ней, может быть стянута в одну точку, не покидая при этом поверхности. Для тора это справедливо не всегда: петля, проходящая через его отверстие, стянется в точку либо при разломе тора, либо при разрыве самой петли. В 1904 году Пуанкаре высказал предположение, что если петля может стягиваться в точку на замкнутой трехмерной поверхности, то такая поверхность гомеоморфна трехмерной сфере. Доказательство этой гипотезы оказалось чрезвычайно сложной задачей.
Сразу уточним: упомянутая нами формулировка проблемы Пуанкаре говорит вовсе не о трехмерном шаре, который мы можем представить себе без особого труда, а о трехмерной сфере, то есть о поверхности четырехмерного шара, который представить себе уже гораздо труднее. Но в конце 1950-х годов неожиданно выяснилось, что с многообразиями высоких размерностей работать гораздо легче, чем с трех- и четырехмерными. Очевидно, отсутствие наглядности — далеко не главная трудность, с которой сталкиваются математики в своих исследованиях.
Задача, подобная проблеме Пуанкаре, для размерностей 5 и выше была решена в 1960 году Стивеном Смэйлом (Stephen Smale), Джоном Стэллингсом (John Stallings) и Эндрю Уоллесом (Andrew Wallace). Подходы, использованные этими учеными, оказались, однако, неприменимы к четырехмерным многообразиям. Для них проблема Пуанкаре была доказана лишь в 1981 году Майклом Фридманом (Michael Freedman). Трехмерный же случай оказался самым сложным; его решение и предлагает Григорий Перельман.
Необходимо отметить, что у Перельмана есть соперник. В апреле 2002 года профессор математики британского университета Саутгемптон Мартин Данвуди предложил свой метод решения проблемы Пуанкаре и теперь ожидает вердикт от института Клэя.
Специалисты считают, что решение проблемы Пуанкаре позволит сделать серьезный шаг в математическом описании физических процессов в сложных трехмерных объектах и даст новый импульс развитию компьютерной топологии. Метод, который предлагает Григорий Перельман, приведет к открытию нового направления в геометрии и топологии. Петербургский математик вполне может претендовать на премию Филдса (аналог Нобелевской премии, которую по математике не присуждают).
Между тем, некоторые находят поведение Григория Перельмана странным. Вот что пишет британская газета «Гардиан»: «Скорее всего, подход Перельмана к разгадке проблемы Пуанкаре верный. Но не все так просто. Перельман не предоставляет доказательств того, что работа издана в качестве полноценной научной публикации (препринты таковой не считаются). А это необходимо, если человек хочет получить награду от института Клэя. Кроме того, он вообще не проявляет интереса к деньгам».
Видимо, для Григория Перельмана, как для настоящего ученого, деньги — не главное. За решение любой из так называемых «задач тысячелетия» истинный математик продаст душу дьяволу.
ГРИГОРИЙ ПЕРЕЛЬМАН |
Родился 13 июня 1966 года в Ленинграде, в семье служащих. Окончил знаменитую среднюю школу № 239 с углубленным изучением математики. В 1982 году в составе команды советских школьников участвовал в Международной математической олимпиаде, проходившей в Будапеште. Был без экзаменов зачислен на матмех Ленинградского государственного университета. Побеждал на факультетских, городских и всесоюзных студенческих математических олимпиадах. Получал Ленинскую стипендию. Окончив университет, Перельман поступил в аспирантуру при Санкт-Петербургском отделении Математического института им.В.А.Стеклова. Кандидат физико-математических наук. Работает в лаборатории математической физики. |
[http://lenta.ru/articles/2004/09/12/poincare/]
Китайские математики опубликовали полное доказательство гипотезы Пуанкаре, сформулированной в 1904 году, передает новостное агентство Xinhua. Гипотеза, касающаяся классификации многомерных поверхностей (а точнее, многообразий), входила в число «проблем тысячелетия», за решение каждой из которых американский Институт Клэя назначил награду в миллион долларов.
Согласно Пуанкаре, любая замкнутая трехмерная «поверхность без дыр» (односвязное многообразие) эквивалентна трехмерной сфере, то есть поверхности четырехмерного шара. Сам Пуанкаре, автор математического аппарата эйнштейновской теории, представил первое обоснование, но позже обнаружил в собственных рассуждениях ошибку. Гипотезу в такой формулировке доказал в 2003 году российский математик Григорий Перельман, 70-страничную работу которого эксперты проверяют до сих пор. Другие случаи (размерности четыре и выше) были рассмотрены ранее.
По словам авторов, новая 300-страничная статья в Asian Journal of Mathematics не является независимой и опирается в первую очередь на результаты Перельмана. Чжу Сипин и Цао Хуайдун утверждают, что теперь ликвидировали ряд трудностей, способы преодоления которых Перельманом были только намечены. Известно, что в работе над доказательством также участвовал Шин-Тунь Яу, топологические труды которого (в частности, теория многообразий Калаби-Яу) считаются ключевыми для современной теории струн. Новая работа, отмечают специалисты, также потребует длительной перепроверки.
[http://www.inauka.ru/news/article64629.html]
Александров А.Д., Нецветаев Н.Ю. Геометрия. М.: Наука, 1990
[http://alexandr4784.narod.ru/antoppdf/519-527.pdf]
[http://alexandr4784.narod.ru/antoppdf/527-532.pdf]
[http://www.ega-math.narod.ru/Nquant/Space.htm]
Приложение к реферату 2: [http://wsyachina.narod.ru/astronomy/configuration_universe.html]
studfiles.net
Теория, теорема Пуанкаре — Перельмана: VIKENT.RU
Теория, теорема Пуанкаре — Перельмана в популярном изложении по В.А. Успенскому
«Проблема, которую решил Перельман, состоит в требовании доказать гипотезу, выдвинутую в 1904 году великим французским математиком Анри Пуанкаре (1854-1912) и носящую его имя. О роли Пуанкаре в математике трудно сказать лучше, чем это сделано в энциклопедии: «Труды Пуанкаре в области математики, с одной стороны, завершают классическое направление, а с другой — открывают пути к развитию новой математики, где наряду с количественными соотношениями устанавливаются факты, имеющие качественный характер» (БСЭ, изд. 3-е, т. 2). Гипотеза Пуанкаре как раз и имеет качественный характер — как и вся та область математики (а именно топология), к которой она относится и в создании которой Пуанкаре принял решающее участие.
На современном языке гипотеза Пуанкаре звучит так: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере.
В следующих абзацах мы постараемся хотя бы частично и очень приблизительно разъяснить смысл этой устрашающей словесной формулы. Для начала заметим, что обычная сфера, которая есть поверхность обычного шара, двумерна (а сам шар — тот трёхмерен). Двумерная сфера состоит из всех точек трёхмерного пространства, равноудалённых от некоторой выделенной точки, называемой центром и сфере не принадлежащей. Трёхмерная сфера состоит из всех точек четырёхмерного пространства, равноудалённых от своего центра (сфере не принадлежащего). В отличие от двумерных сфер трёхмерные сферы недоступны нашему непосредственному наблюдению, и нам представить себе их так же трудно, как Василию Ивановичу из известного анекдота квадратный трёхчлен. Не исключено, однако, что все мы как раз в трёхмерной сфере и находимся, то есть что наша Вселенная является трёхмерной сферой.
В этом состоит значение результата Перельмана для физики и астрономии. Термин «односвязное компактное трёхмерное многообразие без края» содержит указания на предполагаемые свойства нашей Вселенной. Термин «гомеоморфно» означает некую высокую степень сходства, в известном смысле неотличимость. Формулировка в целом означает, следовательно, что если наша Вселенная обладает всеми свойствами односвязного компактного трёхмерного многообразия без края, то она — в том же самом «известном смысле» — и есть трёхмерная сфера.
Понятие односвязности — довольно простое понятие. Представим себе канцелярскую резинку (то есть резиновую нить со склеенными концами) столь упругую, что она, если её не удерживать, стянется в точку. От нашей резинки мы потребуем ещё, чтобы при стягивании в точку она не выходила за пределы той поверхности, на которой мы её расположили. Если мы растянем такую резинку на плоскости и отпустим, она немедленно стянется в точку. То же произойдёт, если мы расположим резинку на поверхности глобуса, то есть на сфере. Для поверхности спасательного круга ситуация окажется совершенно иной: любезный читатель легко найдёт такие расположения резинки на этой поверхности, при которой стянуть резинку в точку, не выходя за пределы рассматриваемой поверхности, невозможно. Геометрическая фигура называется односвязной, если любой замкнутый контур, расположенный в пределах этой фигуры, можно стянуть в точку, не выходя за названные пределы. Мы только что убедились, что плоскость и сфера односвязны, а поверхность спасательного круга не односвязна. Не односвязна и плоскость с вырезанной в ней дырой. Понятие односвязности применимо и к трёхмерным фигурам. Так, куб и шар односвязны: всякий находящийся в их толще замкнутый контур можно стянуть в точку, причём в процессе стягивания контур будет всё время оставаться в этой толще. А вот баранка не односвязна: в ней можно найти такой контур, который нельзя стянуть в точку так, чтобы в процессе стягивания контур всё время находился в тесте баранки. Не односвязен и крендель. Можно доказать, что трёхмерная сфера односвязна.
Надеемся, что читатель не забыл, ещё разницу между отрезком и интервалом, которой обучают в школе. Отрезок имеет два конца, он состоит из этих концов и всех точек, расположенных между ними. Интервал же состоит только из всех точек, расположенных между его концами, сами же концы в состав интервала не входят: можно сказать, что интервал — это отрезок с удалёнными из него концами, а отрезок — это интервал с добавленными к нему концами. Интервал и отрезок являются простейшими примерами одномерных многообразий, причём интервал есть многообразие без края, а отрезок — многообразие с краем; край в случае отрезка состоит из двух концов. Главное свойство многообразий, лежащее в основе их определения, состоит в том, что в многообразии окрестности всех точек, за исключением точек края (которого может и не быть), устроены совершенно одинаково.
При этом окрестностью какой-либо точки А называется совокупность всех точек, расположенных вблизи от этой точки А. Микроскопическое существо, живущее в многообразии без края и способное видеть только ближайшие к себе точки этого многообразия, не в состоянии определить, в какой именно точке оно, существо, находится: вокруг себя оно всегда видит одно и то же. Ещё примеры одномерных многообразий без края: вся прямая линия целиком, окружность. Примером одномерной фигуры, не являющейся многообразием, может служить линия в форме буквы Т: здесь есть особая точка, окрестность которой не похожа на окрестности других точек — это точка, где сходятся три отрезка. Другой пример одномерного многообразия — линия в форме восьмёрки; в особой точке здесь сходятся четыре линии. Плоскость, сфера, поверхность спасательного круга служат примерами двумерных многообразии без края. Плоскость с вырезанной в ней дырой также будет многообразием — а вот с краем или без края, зависит от того, куда мы относим контур дыры. Если мы относим его к дыре, получаем многообразие без края; если оставляем контур на плоскости, получаем многообразие с краем, каковым и будет служить этот контур. Разумеется, мы имели здесь в виду идеальное математическое вырезание, а при реальном физическом вырезании ножницами вопрос, куда относится контур, не имеет никакого смысла.
Несколько слов о трёхмерных многообразиях. Шар вместе со сферой, служащей его поверхностью, представляет собою многообразие с краем; указанная сфера как раз и является этим краем. Если мы удалим этот шар из окружающего пространства, получим многообразие без края. Если мы сдерём с шара его поверхность, получится то, что на математическом жаргоне называется «ошкуренный шар», а в более научном языке — открытый шар. Если удалить открытый шар из окружающего пространства, получится многообразие с краем, и краем будет служить та самая сфера, которую мы содрали с шара. Баранка вместе со своей корочкой есть трёхмерное многообразие с краем, а если отодрать корочку (которую мы трактуем как бесконечно тонкую, то есть как поверхность), получим многообразие без края в виде «ошкуренной баранки». Всё пространство в целом, если понимать его так, как оно понимается в средней школе, есть трёхмерное многообразие без края.
Математическое понятие компактность отчасти отражает тот смысл, какой слово «компактный» имеет в повседневном русском языке: «тесный», «сжатый». Геометрическая фигура называется компактной, если при любом расположении бесконечного числа её точек они накапливаются к одной из точек или ко многим точкам этой же фигуры. Отрезок компактен: для любого бесконечного множества его точек в отрезке найдётся хотя бы одна так называемая предельная точка, любая окрестность которой содержит бесконечно много элементов рассматриваемого множества. Интервал не компактен: можно указать такое множество его точек, которое накапливается к его концу, и только к нему, — но ведь конец не принадлежит интервалу!
За недостатком места мы ограничимся этим комментарием. Скажем лишь, что из рассмотренных нами примеров компактными являются отрезок, окружность, сфера, поверхности баранки и кренделя, шар (вместе со своей сферой), баранка и крендель (вместе со своими корочками). Напротив, интервал, плоскость, ошкуренные шар, баранка и крендель не являются компактными. Среди трёхмерных компактных геометрических фигур без края простейшей является трёхмерная сфера, но в нашем привычном «школьном» пространстве такие фигуры не умещаются. Самое, пожалуй, глубокое из тех понятий, которые связывает между собой гипотеза Пуанкаре, — это понятие гомеоморфии. Гомеоморфия — это наиболее высокая ступень геометрической одинаковости. Сейчас мы попытаемся дать приблизительное разъяснение этому понятию путём постепенного к нему приближения.
Уже в школьной геометрии мы встречаемся с двумя видами одинаковости — с конгруэнтностью фигур и с их подобием. Напомним, что фигуры называются конгруэнтными, если они совпадают друг с другом при наложении. В школе конгруэнтные фигуры как бы не различают, и потому конгруэнтность называют равенством. Конгруэнтные фигуры имеют одинаковые размеры во всех своих деталях. Подобие же, не требуя одинаковости размеров, означает одинаковость пропорций этих размеров; поэтому подобие отражает более сущностное сходство фигур, нежели конгруэнтность. Геометрия в целом — более высокая ступень абстракции, нежели физика, а физика — чем материаловедение.
Возьмём, к примеру, шарик подшипника, биллиардный шар, крокетный шар и мяч. Физика не вникает в такие детали, как материал, из которого они сделаны, а интересуется лишь такими свойствами, как объём, вес, электропроводность и т. п. Для математики — все они шары, различающиеся только размерами. Если шары имеют разные размеры, то они различаются для метрической геометрии, но все они одинаковы для геометрии подобия. С точки зрения геометрии подобия одинаковы и все шары, и все кубы, а вот шар и куб — не одинаковы.
А теперь посмотрим на тор. Top — эта та геометрическая фигура, форму которой имеют баранка и спасательный круг. Энциклопедия определяет тор как фигуру, полученную вращением круга вокруг оси, расположенной вне этого круга. Призываем благосклонного читателя осознать, что шар и куб «более одинаковы» между собой, чем каждый из них с тором. Наполнить это интуитивное осознание точным смыслом позволяет следующий мысленный эксперимент. Представим себе шар сделанным из материала столь податливого, что его можно изгибать, растягивать, сжимать и, вообще, деформировать как угодно, — нельзя только ни разрывать, ни склеивать. Очевидно, что шар тогда можно превратить в куб, но вот в тор превратить невозможно. Толковый словарь Ушакова определяет крендель как выпечку (буквально: как сдобную витую булку) в форме буквы В. При всём уважении к этому замечательному словарю, слова «в форме цифры 8» кажутся мне более точными; впрочем, с той точки зрения, которая выражена в понятии гомеоморфии, и выпечка в форме цифры 8, и выпечка в форме буквы В, и выпечка в форме фиты имеют одну и ту же форму. Даже если предположить, что хлебопёки сумели получить тесто, обладающее вышеуказанными свойствами податливости, колобок невозможно — без разрывов и склеиваний! — превратить ни в баранку, ни в крендель, как и последние две выпечки друг в друга. А вот превратить шарообразный колобок в куб или в пирамиду — можно. Любезный читатель, несомненно, сумеет найти и такую возможную форму выпечки, в которую нельзя превратить ни колобок, ни крендель, ни баранку.
Не назвав этого понятия, мы уже познакомились с гомеоморфией. Две фигуры называются гомеоморфными, если одну можно превратить в другую путём непрерывной (т. е. без разрывов и склеивании) деформации; сами такие деформации называются гомеоморфизмами. Мы только что выяснили, что шар гомеоморфен кубу и пирамиде, но не гомеоморфен ни тору, ни кренделю, а последние два тела не гомеоморфны между собой. Просим читателя понимать, что мы привели лишь приблизительное описание понятия гомеоморфии, данное в терминах механического преобразования.
Коснёмся философского аспекта понятия гомеоморфии. Представим себе мыслящее существо, живущее внутри какой-либо геометрической фигуры и не обладающее возможностью посмотреть на эту фигуру извне, «со стороны». Для него фигура, в которой оно живёт, образует Вселенную. Представим себе также, что когда объемлющая фигура подвергается непрерывной деформации, существо деформируется вместе с нею. Если фигура, о которой идёт речь, является шаром, то существо никаким способом не может различить, пребывает ли оно в шаре, в кубе или в пирамиде. Однако для него не исключена возможность убедиться, что его Вселенная не имеет формы тора или кренделя. Вообще, существо может установить форму окружающего его пространства лишь с точностью до гомеоморфии, то есть оно не в состоянии отличить одну форму от другой, коль скоро эти формы гомеоморфны.
Для математики значение гипотезы Пуанкаре, превратившейся теперь из гипотезы в теорему Пуанкаре — Перельмана, огромно (не зря ведь за решение проблемы был предложен миллион долларов), равно как огромно и значение найденного Перельманом способа её доказательства, но объяснить это значение здесь — вне нашего умения. Что же касается космологической стороны дела, то, возможно, значимость этого аспекта была несколько преувеличена журналистами.
Впрочем, некоторые авторитетные специалисты заявляют, что осуществлённый Перельманом научный прорыв может помочь в исследовании процессов формирования чёрных дыр. Чёрные дыры, кстати, служат прямым опровержением положения о познаваемости мира — одного из центральных положений того самого передового, единственно верного и всесильного учения, которое 70 лет насильственно вдалбливалось в наши бедные головы. Ведь, как учит физика, никакие сигналы из этих дыр не могут к нам поступать в принципе, так что узнать, что там происходит, невозможно. О том, как устроена наша Вселенная в целом, мы вообще знаем очень мало, и сомнительно, что когда-нибудь узнаем. Да и сам смысл вопроса о её устройстве не вполне ясен. Не исключено, что этот вопрос относится к числу тех, на которые, согласно учению Будды, не существует ответа. Физика предлагает лишь модели устройства, более или менее согласующиеся с известными фактами. При этом физика, как правило, пользуется уже разработанными заготовками, предоставляемыми ей математикой.
Математика не претендует, разумеется, на то, чтобы установить какие бы то ни было геометрические свойства Вселенной. Но она позволяет осмыслить те свойства, которые открыты другими науками. Более того. Она позволяет сделать более понятными некоторые такие свойства, которые трудно себе вообразить, она объясняет, как такое может быть. К числу таких возможных (подчеркнём: всего лишь возможных!) свойств относятся конечность Вселенной и её неориентируемость.
Долгое время единственной мыслимой моделью геометрического строения Вселенной служило трёхмерное евклидово пространство, то есть то пространство, которое известно всем и каждому из средней школы. Это пространство бесконечно; казалось, что никакие другие представления и невозможны; помыслить о конечности Вселенной казалось безумием. Однако ныне представление о конечности Вселенной не менее законно, чем представление о её бесконечности. В частности, конечна трёхмерная сфера. От общения с физиками у меня осталось впечатление, что одни отвечают «скорее всего. Вселенная бесконечна», другие же — «скорее всего, Вселенная конечна».
Успенский В.А., Апология математики, или о математике как части духовной культуры, журнал «Новый мир», 2007 г., N 12, с. 141-145.
vikent.ru
Доказательство гипотезы Пуанкаре Григорием Перельманом
Транскрипт
1 Доказательство гипотезы Пуанкаре Григорием Перельманом. Хорошо известна связь между топологией и метрической геометрией замкнутых двумерных поверхностей: на всякой такой поверхности можно ввести метрику постоянной кривизны, причем знак последней совпадает со знаком эйлеровой характеристики поверхности (положителен для сферы, ноль для тора и отрицателен для поверхностей, описываемых поверхностными интегралами выше первого рода). Около 1980 года Уильям Тѐрстон высказал гипотезу, что подобным образом, только значительно сложнее, обстоит дело с трехмерными многообразиями. Он описал восемь однородных трехмерных римановых геометрий (три геометрии постоянной кривизны и еще пять, однородных, но не изотропных) и обоснованно предположил, что всякое компактное трехмерное многообразие можно определенным образом разбить на куски, в каждом из которых можно ввести одну из восьми модельных геометрий. Гипотеза геометризации Тѐрстона включает в себя в качестве частного случая гипотезу Пуанкаре о том, что связное односвязное ориентируемое трехмерное многообразие гомеоморфно сфере. В течение 25 лет над программой геометризации трехмерной топологии работало множество математиков. Ими было получено большое количество частных результатов, но в целом гипотеза никак не поддавалась, (особое сопротивление оказывали эллиптический и гиперболический случаи). В цикле из трех препринтов гг. Г. Перельман предложил доказательство гипотезы геометризации, основанное на исследовании эволюции риманова многообразия под действием потока Риччи. В 2006 году две независимые группы экспертов закончили изучение работ Перельмана, пришли к выводу, что доказательство правильное и опубликовали пространные тексты, в которых восполнены детали, отсутствовавшие в сжатых оригинальных препринтах. В докладе было дано введение в трехмерную топологию, описана гипотеза геометризации и схематично рассказано о геометрической части рассуждений Г. Перельмана. Последним великим достижением чистой математики называют доказательство петербуржца Григория Перельмана в годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые объясняются так, чтобы их общий смысл стал понятен нематематикам (т.е. читателям, окончившим среднюю школу, и кое-что из школьной математики еще помнят). Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т.е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно — однозначное и взаимно-непрерывное соответствие. Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией: Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором ), так и для заполненных тел (трехмерных многообразий с краем). Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы. 1. Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий 1
2 может служить, во-первых, всѐ трехмерное пространство, обозначаемое R3, а также любые открытые множества точек в R3, к примеру, внутренность полнотория (бублика). Если рассмотреть замкнутое полноторие, т.е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем — у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика. 2. Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы. 3. Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязная (кольцевую резинку, как угодно приложенную к поверхности шара, можно плавной деформацией стянуть в одну точку, не отрывая резинки от шара). С другой стороны, окружность и тор неодносвязные. 4. Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки. Размерность многообразия S — это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т.е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т.д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна. Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий, поскольку у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка. Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые (см. пункт 1) многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности. Не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна поверхность, которую нельзя вложить в пространство без самопересечений. На следующем рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? 2
3 Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно. Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т.е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S3 выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S3 стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т.е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь. Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R3, что облегчает их визуализацию. Для трехмерной сферы S3 (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение. По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S3 это при помощи одноточечной компактификации. А именно, трехмерная сфера S3 представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R3. 3
4 Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность одномерный аналог сферы. Подобным же образом, если возьмем бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S2. Эту процедуру можно наблюдать при помощи стереографической проекции. В каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P’: Таким образом, сфера S2 без одной точки на попюсе это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу S3. только для этого осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. И это дает повод для всевозможных спекуляций о роли Бога. Поэтому ограничимся словесным описанием одноточечной компактификации пространства R3 Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z ) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т.е. каждая пространственная прямая замыкается в окружность)(см. пункт 4). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S3. И роль Бога исчезает. Легко понять, что сфера S3 односвязная. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R3, которая легко стягивается в точку посредством гомотетий, т.е. непрерывного сжатия по всем трем направлениям. Для понимания, как устроено многообразие S3, весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R3 выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S3 разбивается на два полнотория, имеющих общую границу тор. Вот как это можно понять. Вложим тор в R3 как обычно, в виде круглого бублика, и проведем вертикальную прямую ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет полноторие по двум кругам (показанным на рисунке зеленым цветом). Дополнительная часть плоскости, разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, 4
5 выделенная более жирно, потому что в сфере S3 прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомеоморфное полноторию, только выглядящее необычно. В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей окружностей, составляющих обычное полноторие. Чтобы было с чем сравнивать 3-сферу, приведем еще один пример компактного 3 — многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб: В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A’ это одна и та же точка, а B и B’ тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб-это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A’ в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора. Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления. Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная. На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA’ на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A’ обязаны двигаться по своим граням, оставаясь строго, друг напротив друга (иначе кривая разомкнется). Итак, мы видим, что бывают односвязные и неодносвязные компактные 3 — многообразия. Перельман доказал, что односвязное многообразие ровно одно. Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т.е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который 5
6 высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, в трехмерном случае поток Риччи способен портить многообразие, т.е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, т. е. в конце концов, оно превращается в круглую сферу. Но нужно объяснить, наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому ограничимся описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость. Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она плавная, кривизна будет меньше. Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение не зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например: окружность радиуса единице имеет постоянную положительную кривизну, равную единице (если считать ее в радианах). Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот этот пример изображен на рисунке. Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т.е. превращается, в конце концов, в окружность с отсутствием особых точек. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, простой способ доказательства иллюстрирует, что происходит в размерности S3). Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и общую гипотезу геометризации Тѐрстона, которая в известном смысле 6
7 описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи. То есть наблюдаемая нами реальность, это трехмерное евклидовое многообразие. И это основной вывод из работ Тѐрстона, Гамильтона — Перельмана. Для изложенного обозрения использованы работы Сергея Дужина, докт. физ.-мат. наук, Санкт-Петербургского отделения Математического института РАН 7
docplayer.ru
Научно-исследовательская работа на тему «Гипотеза Пуанкаре»

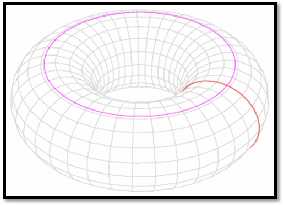
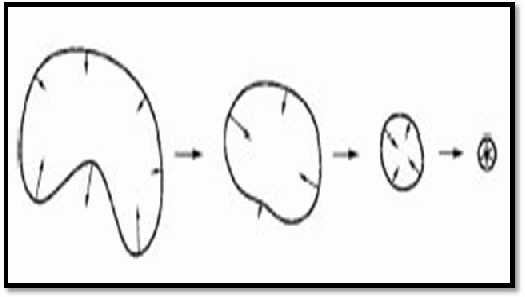





 Научно-практическая конференция
Научно-практическая конференция
Номинация «Шаги в науку»
Секция: математика
«Пластилиновая» гипотеза или доказательство на миллион.
Выполнила: Асланбекова Марьям, ученица 9 А класса.
Научный руководитель: Асланбекова Лида Сайдаровна,
учитель математики МБОУ «СОШ №50» г. Грозного.
Оглавление:
1.Введение………………………………………………………………………..3
1.1.Актуальность работы……………………………………4
1.2.Выдвижение гипотезы…………………………………..5
1.3.Цели и задачи проекта……………………………….….5
1.4.Социологический опрос…………………………………6
2.Основная часть:
2.1.Немного истории………………………………………..9
2.2.Гипотеза Пуанкаре………………………………………….11
2.3.Кружка, пончик и немного топологии…………………13
2.4.Доказательство длиною в век………………………………14
2.5.Григорий Перельман.
Как не стать миллионером…………………………………16
2.6.Значение гипотезы Пуанкаре…………………………………..17
2.7.Семь величайших математических
загадок тысячелетия……………………………………………18
3.Заключение……………………………………………….…21
3.1.Выводы……………………………………………….….21
3.2.Практическое применение работы…………………….21
4.Литература………………………………………………….22
5.Приложение (Буклет)………………………………………23
1.Введение
Хорошая теория – самая практичная вещь на свете.
Оглянитесь вокруг. Окружающие нас предметы, как и мы сами, представляют собой набор частиц, перемещающихся в трехмерном пространстве, которое простирается во всех направлениях на многие миллиарды световых лет. Ученые, благодаря трудам которых произошли колоссальные сдвиги в естествознании ХХ века, также отдавали должное математическому устройству мира. Анри Пуанкаре всеобщий характер математических законов выразил во фразе: «Математика — это искусство называть разные вещи одним и тем же именем». Арнольд Зоммерфельд, один из творцов квантовой механики и современной математической физики, утверждал: «Мы все яснее видим, что наиболее общая математическая формулировка одновременно является и физически наиболее плодотворной». Схожим образом рассуждал и Поль Дирак: «Ситуацию, вероятно, можно было бы описать, сказав, что Бог является математиком очень высокого ранга и что он при построении Вселенной использовал математику высшего уровня». О необыкновенной силе и красоте математики размышлял Юджин Вигнер: «Математический язык удивительно хорошо приспособлен для формулировки физических законов, это чудесный дар, который мы не понимаем и которого не заслуживаем. Нам остается лишь благодарить за него судьбу и надеяться, что и в своих будущих исследованиях мы сможем по-прежнему пользоваться им». Представление о том, что мир живет по законам математики, характерно и для Средневековья. В это время широкое распространение получило сочинение Клавдия Птолемея «Великое математическое построение по астрономии в 13 книгах», созданное во II веке, более известное под своим арабским названием «Альмагест». В нем утверждалось, что небосвод имеет идеальную форму — форму сферы***, форма Земли также идеальна, это шар, помещенный в центр мира; с помощью набора идеальных круговых движений объясняется
***Главная идея гипотезы Пуанкаре
видимое движение планет. Форма, выбранная для описания законов неба, умозрительная, она предложена из соображений красоты и симметрии, а не получена экспериментально.
1.1.Актуальность работы
Часто, беседуя со старшеклассниками об исследовательских работах по математике, слышу следующее: «Что можно нового открыть в математике?». А действительно: может быть все великие открытия сделаны, а теоремы уже доказаны?
Проблема, о которой пойдет речь, выбивается из ряда других проблем математики 2000 года: лишь она одна считается уже решенной. Приоритет Григория Перельмана — нашего соотечественника, доказавшего гипотезу Пуанкаре, — неоспорим, его доказательство признано ведущими экспертами мира.
Об этой почти детективной истории я узнала недавно. Стала спрашивать у друзей и учителей, к сожалению, многие даже не слышали о гипотезе Пуанкаре, а в Интернете об этом пишут мало и непонятно. Таким образом, я стала читать и разбираться в гипотезе, и к своему великому удивлению, узнала, что в мире математики существует определенный ряд загадок, которые ждут своего часа. Очень жаль, что телевидение и средства массовой информации, которые уделяют столько внимания кино, искусству, литературе и всяким развлечениям, так мало проливают свет на такие необходимые для человека науки как математика, физика, на их проблемы и достижения.
1.2.Выдвижение гипотезы
Неужели гипотеза Пуанкаре (доказательство Перельмана) подтверждает теоретические предположения ученых о строении Вселенной со времен создания мира!
Гипотеза Пуанкаре настолько сложна для понимания простому обывателю, что я взяла на себя смелость изучить самой и рассказать о ней и других математических задачах тысячелетия своим сверстникам.
Таким образом, ко мне пришла идея о создании этого проекта.
Все ли великие открытия в математике сделаны, а теоремы доказаны?
1.3.Цели и задачи проекта
Итак, целью моей работы является познакомиться с величайшими математическими задачами тысячелетия, в том числе с гипотезой Пуанкаре и поделиться информацией со своими сверстниками, создать информационный продукт в виде презентации, буклета.
А для того, чтобы достичь поставленную цель мне следует решить следующие задачи:
Изучить гипотезу Пуанкаре.
Познакомиться с топологией.
Рассмотреть доказательство Перельмана.
Исследовать роль гипотезы Пуанкаре в изучении космоса и строении мироздания.
Провести социологический опрос среди учащихся СОШ №50.
Изготовить информационный буклет.
1.4.Социологический опрос.
Во время исследований я провела социологический опрос, чтобы понять, насколько мои сверстники знакомы с данной темой.
Было проведено анкетирование среди учащихся МБОУ «СОШ №50».
А также на сайте я разместила онлайн-анкету «Задачи Тысячелетия», на которую ребята могут ответить по ссылке:
http://anketolog.ru/s/118101/qjlOsbIs
Анкета состояла из следующих вопросов:
Есть ли в математике до конца не исследованные области?
Каков список великих математических задач тысячелетия?
Знаете ли Вы, за что хотели наградить миллионом долларов Григория Перельмана?
Результат превзошел все ожидания.
1. Вопрос: Есть ли в математике до конца не исследованные области? Скорее нет, чем да- 55%
Скорее да, чем нет- 20%
Нет- 10%
Да- 15%
Диаграмма №1
2. Вопрос: Каков список великих математических задач тысячелетия?
Не знаю-83%
Слышал, что существует, но не знаю-10%
Не слышал, что существует- 7%
Да-0%
Диаграмма №2
3. На вопрос: знаете ли Вы, за что хотели наградить миллионом долларов Григория Перельмана, ответили так.
Нет-70%
Знаю, но не понимаю суть-22%
Да-8%
Диаграмма №3
Анализ анкетирования. Судя по результатам анкетирования, многие практически не посвящены в вопросы, математических задач тысячелетия. Но порадовали ответы оптимистично настроенных и заинтересованных ребят. Это дает мне стимул для дальнейших исследований.
2.1.Немного истории
Начнем с 19 века. В 1887 году Пуанкаре представил работу на математический конкурс, посвященный 60-летию короля Швеции Оскара II. В ней обнаружилась ошибка, которая привела к появлению теории хаоса.
Вообще говоря, в математике можно сформулировать большое количество сложных утверждений. Однако, что делает ту или иную гипотезу великой, отличает ее от остальных? Как это ни странно, но великую гипотезу отличает большое количество неправильных доказательств, в каждом из которых есть по великой ошибке — неточности, которая зачастую приводит к возникновению целого нового раздела математики.
Так, изначально Анри Пуанкаре, который отличался помимо всего прочего умением совершать гениальные ошибки, сформулировал гипотезу немного в другом виде, чем пишут сейчас. И в 1904 году он сформулировал гипотезу уже в современном виде.
Надо сказать, что особого ажиотажа среди коллег гипотеза тогда не вызвала. Так было до 1934 года, когда британский математик Джон Генри Уайтхед представил свой вариант доказательства гипотезы. Очень скоро, однако, он сам нашел в рассуждениях ошибку.
После этого за гипотезой постепенно закрепилась слава крайне сложной задачи. Многие великие математики пытались взять ее приступом. Например, американский Эр Аш Бинг (R.H.Bing), математик, у которого (абсолютно официально) вместо имени в документах были записаны инициалы. Он предпринял несколько безуспешных попыток доказать гипотезу.
Были среди ученых и люди, положившие жизнь на доказательство этого математического факта.
Работа многих ученых, пытавшихся доказать гипотезу Пуанкаре, привела к возникновению целого направления в математике и может считаться в этом смысле успешной и значимой, доказать гипотезу Пуанкаре окончательно удалось только россиянину Григорию Перельману.
Анри Пуанкаре был одним из двух сильнейших математиков начала XX в. (другим был Давид Гильберт). Его называли последним универсалом – он успешно работал во всех разделах как чистой, так и прикладной математики. Кроме того, Пуанкаре внес огромный вклад в развитие небесной механики, теорию электромагнетизма, а также в философию науки, о которой написал несколько популярных книг.
Жюль Анри Пуанкаре (1854 – 1912) французский математик, физик, астроном и философ. Занимался решением задач небесной механики: изучение возмущённого движения, теория устойчивости, вопрос о фигурах равновесия жидких масс, что способствовало развитию теории происхождения звёзд путём деления одиночных вращающихся звёзд. Независимо от Эйнштейна выдвинул основные положения специальной теории относительности. Он считается учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг.
Среди его самых крупных достижений:
Создание топологии.
Разработка новых, чрезвычайно эффективных методов небесной механики.
Создание математических основ теории относительности.
В 1900 г. сформулировал топологическую характеристику объекта, названную гомотопией*.
*Чтобы определить гомотопию многообразия, нужно мысленно погрузить в него замкнутую петлю, затем следует выяснить, всегда ли можно стянуть петлю в точку, перемещая ее внутри многообразия. Для тора ответ будет отрицательным: если расположить петлю по окружности тора, то стянуть ее в точку не удастся, т.к. будет мешать «дырка» бублика. Гомотопия* – это количество различных путей, которые могут воспрепятствовать стягиванию петли.
2.2.Гипотеза Пуанкаре
Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002-2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое компактное трехмерное многообразие без края гомеоморфно* сфере S3».
Простыми словами гипотезу Пуанкаре можно изложить так: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить сферу.
Главным «действующим лицом» гипотезы является трехмерная сфера.
Оказывается, что любое замкнутое кривое пространство ведет себя при такой эволюции подобным же образом, т.е. превращается, в конце концов, в сферу.
Объясняя гипотезу Пуанкаре, начинают так: представьте себе двухмерную сферу — возьмите диск и натяните его на шар. Так, чтобы окружность диска оказалась собранной в одной точке.
Аналогичным образом, к примеру, можно стянуть шнуром спортивный рюкзак. В итоге получится сфера: для нас — трехмерная, но с точки зрения математики — всего лишь двухмерная. Затем предлагают натянуть тот же диск на бублик. Вроде бы получится. Но края диска сойдутся в окружность, которую уже не стянуть в точку — она разрежет бублик.
Так вот, легко видеть, что на сфере любая петля стягиваема (как это примерно выглядит, можно посмотреть), а вот для тора это уже не так: на бублике есть целых две петли — одна продета в дырку, а другая обходит дырку «по периметру», — которые нельзя стянуть.
На этой картинке примеры не стягиваемых петель показаны красным и фиолетовым цветом соответственно.
Грусть на лице этого животного является следствием осознания того, что желаемый кусочек сыра находится на нестягиваемой петле.
В формулировке гипотезы я думаю не все понятно обычному школьнику. Постараюсь объяснить общий смысл некоторых понятий.
Начнем с понятия гомеоморфизма, центрального в топологии*.
2.3.Кружка, бублик и немного топологии
Топологию* часто определяют, как «резиновую геометрию», т.е. как науку о свойствах геометрических фигур, которые не меняются при плавных деформациях без разрывов и склеек.
Чтобы глубже понять гипотезу Пуанкаре и доказательство Перельмана, следует поближе познакомиться с топологией. В этом разделе математики форма объекта не имеет значения, как будто он сделан из теста, которое можно как угодно растягивать, сжимать и изгибать. Зачем же нам задумываться о вещах или пространствах из воображаемого теста? Дело в том, что точная форма объекта – расстояние между всеми его точками – относится к структурному уровню, который называют геометрией. Рассматривая объект из теста, топологи выявляют его фундаментальные свойства, не зависящие от геометрической структуры. Изучение топологии похоже на поиск наиболее общих черт, присущих людям, методом рассмотрения «пластилинового человека», которого можно превратить в любого конкретного индивида.
Главную идею проще всего объяснить на классическом примере кружки и бублика. Кружку можно превратить в бублик непрерывной деформацией:
Эти рисунки наглядно показывают, что кружка гомеоморфна бублику (т.е. можно продеформировать в….), причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).
2.4.Доказательство длиною в век…
Григорий Яковлевич Перельман родился и вырос в Ленинграде, учился в знаменитой 239-й школе. В 1982 году выиграл Международную математическую олимпиаду, набрав максимально возможное количество баллов. Получил степень кандидата наук, затем некоторое время работал в Петербургском отделении математического института РАН, в конце восьмидесятых уехал в США, где работал до середины девяностых, а затем вернулся в Россию.
Перельман на долгих семь лет (с возвращения в Россию до 2002 года) практически перестал публиковаться и вообще почти ничем не напоминал о себе. Никто не знал, над чем он работал. Затем, как гром среди ясного неба появились статьи, содержащие доказательство гипотезы Пуанкаре, в ноябре 2002 года. В 2003 году Григорий Яковлевич дополнил первый препринт еще одним, в котором подробнее изложил технические подробности доказательства. Кроме того, он выступил с лекциями, где комментировал свои идеи. Казалось бы, больше ничего не нужно: проверяйте доказательство и платите миллион. Первые результаты проверки идей российского математика появились в 2006 году — крупные геометры Брюс Кляйнер и Джон Лотт из Мичиганского университета опубликовали работу, по размерам больше напоминающей книгу — 213 страниц. В этой работе ученые тщательно проверили все выкладки Перельмана, подробно пояснив различные утверждения, которые в работе российского математика были лишь вскользь обозначены. Вердикт исследователей был однозначен: доказательство абсолютно верное.
2.5.Григорий Перельман. Как не стать миллионером.
В 2002-2003 годах русский математик Григорий Перельман опубликовал в интернете доказательство гипотезы Пуанкаре, которое не давалось ни одному из его коллег в течение почти ста лет. Перельмана ждали слава, многочисленные награды и приз в $1 млн, назначенный за решение этой задачи благотворительным Институтом Клэя. Перельман, однако, отказался и от почестей и от денег, а через несколько лет и вовсе ушел из математики. Заместитель главного редактора проекта «Сноб» Маша Гессен написала книгу, посвященную математику. Первоначально книга вышла на английском языке в США, теперь перевод книги «Безупречная строгость. Григорий Перельман: гений и задача тысячелетия» выходит на русском языке в издательстве CORPUS (в переводе Ильи Кригера).
Это не первый случай отказа Перельмана от премий:
1996 год — премия Европейского конгресса математиков
2006 год — Филдсовская премия
2010 год — Премия тысячелетия
Российский математик Григорий Перельман не прибыл на церемонию награждения в Париж, где ему должны были вручить премию в 1 млн долларов, присужденную ему американским Математическим институтом Клэя.
В отсутствие Перельмана символический сертификат премии был передан другому российскому математику — Михаилу Громову, работающему во Франции, и Франсуа Пуанкаре, внуку создателя топологической гипотезы, предполагающей, что пространство является трехмерной сферой с точностью до деформации.
Григорий Перельман живет затворником вместе с мамой в обычной панельной многоэтажке на окраине Санкт-Петербурга. Ничем, кроме математики, не интересуется, контакты с окружающим миром сводит к минимуму и с прессой категорически не общается.
Похоже, что Михаил Громов, российский геометр, — понял логику Перельмана: «Чтобы сделать великую работу, вы должны иметь чистый разум. Вы можете думать только о математике. Все остальное — человеческие слабости. Принятие премий показывает слабость».
Кинокомпания «Президент-фильм» с согласия Перельмана планирует снять о нем художественную ленту «Формула Вселенной». Математик и пошёл-то на контакт ради этого фильма, который будет не о нём, а о сотрудничестве и противоборстве трех основных мировых математических школ: российской, китайской и американской, наиболее продвинувшихся по стезе изучения и управления Вселенной. На вопрос о миллионе, который так волновал всех удивлённых и любопытных, Перельман ответил: «Я знаю, как управляют Вселенной. И скажите – зачем же мне бежать за миллионом?»
2.6.Значение гипотезы Пуанкаре.
«Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Играет свою роль это открытие и в развитии нанотехнологий.
И здесь уместно сказать об одной особенности современной математики: она изучает искусственно изобретенные объекты. Нет в природе четырехмерных пространств, нет групп, полей и колец, свойства которых усиленно изучают математики. И если в технике постоянно создаются новые аппараты, всевозможные устройства, то в математике создаются их аналоги — логически возможные устройства, логические приемы для мыслительной деятельности человека, для аналитиков в любой области науки. И всякая математическая теория, если она строгая, рано или поздно находит применение. К примеру, многие поколения математиков и философов пытались аксиоматизировать философию. В результате этих попыток была создана теория булевых функций, названных по имени ирландского математика и философа Джорджа Буля. Эта теория стала ядром кибернетики и общей теории управления, которые вместе с достижениями других наук привели к созданию компьютеров, современных морских, воздушных и космических кораблей. Таких примеров история математики дает десятки.
Крупномасштабная геометрия Вселенной представляет собой фундаментальную проблему космологии, особенно важны ее пространственная кривизна и топология. Уравнения Эйнштейна для гравитационного поля определяют лишь локальные свойства пространства-времени, но не глобальную структуру Вселенной в целом. Гипотеза Пуанкаре предполагает, что пространство Вселенной в больших масштабах обладает тривиальной топологией и при этом подразумевается, что она имеет бесконечный объем. При рассмотрении различных сценариев инфляционного расширения эти свойства нашего космоса определяются начальными условиями, возникшими в момент Большого взрыва.
Из доказательства Перельмана следует, что Вселенная имеет форму сферы и стремится в точку, следовательно, гипотеза о Большом взрыве вполне имеет место быть. Поэтому доказательство гипотезы Пуанкаре играет роль не только в описании формы Вселенной, но и помогает сделать прорыв в развитии теории происхождения Вселенной.
2.7.Семь величайших математических загадок тысячелетия.
8 августа 1900 года на международном математическом конгрессе в Париже математик Дэвид изложил список проблем, которые, как он полагал, предстояло решить в ХХ веке. В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма, с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным.
По примеру Гилберта в конце прошлого века многие математики пытались сформулировать подобные стратегические задачи на ХХI век. Один из таких списков приобрел широкую известность благодаря бостонскому миллиардеру Лэндону Клэю. В 1998 году на его средства в Кембридже (Массачусетс, США) был основан Математический институт Клэя (Clay Mathematics Institute) и установлены премии за решение ряда важнейших проблем современной математики. 24 мая 2000 года эксперты института выбрали семь проблем — по числу миллионов долларов, выделенных на премии. Список получил название Millennium Prize Problems.
Институт математики Клея объявил о награде в $1 млн за решение каждой из этих главных математических проблем.
Уравнение Навье-Стксао о турбулентных потоках, 1822 [гидроаэродинамика]. Решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Это позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.
Гипотеза Римана, 1859 [теория чисел]. Считается, что распределение простых чисел среди натуральных не подчиняется никакой закономерности. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
Гипотеза Пуанкаре***, 1904 [топология или геометрия многомерных пространств]: всякое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере [т.е. наша Вселенная — трехмерная сфера?].
Гипотеза Ходжа, 1941 [алгебра, топология]. В ХХ веке математики открыли мощный метод исследования формы сложных объектов — использование вместо самого объекта простых «кирпичиков», которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких «кирпичиков» и объектов.
Теория Янга-Миллса, 1954 [связь геометрии с квантовой физикой]. Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга-Миллса следовало существование частиц, которые действительно наблюдались в лабораториях, поэтому теория Янга — Миллса принята большинством физиков, несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.
Гипотеза Берча и Свиннертона-Дайера, 1960 [алгебра и теория чисел]. Связана с описанием множества решений некоторых алгебраических уравнений от нескольких переменных с целыми коэффициентами. Примером подобного уравнения является выражение x2 + y2 = z2.
Гипотеза Кука, 1971 [математическая логика и кибернетика]. Эта проблема — также одна из нерешенных задач логики и информатики. Ее решение революционно изменило бы основы криптографии [также как и доказательство гипотезы Римана].
***Гипотеза Пуанкаре считается доказанной на сегодняшний день.
3. Заключение
3.1.Выводы.
Гипотеза подтвердилась: действительно, в математике есть много нерешенных задач и недоказанных теорем.
Впереди нас ждут уникальные эксперименты, научные открытия, прорывы в самых современных научных сферах. Главное, чтобы это давало дополнительный стимул развития нашей стране.
Как бы ни сложилось мое будущее, какую бы профессию не выбрала, я уверена, что работа над этим проектом является для меня первым, но уже уверенным шагом в мир большой науки.
Мы надеемся, что задачи тысячелетия будут решены в ближайшее время и это принесет мировой науке только пользу!!!
Итак, к концу своего исследования, я пришла в следующим выводам:
Математика является необъятной наукой.
В школе нужно всячески повышать познавательный интерес учащихся к математике.
Все средства массовой информации должны способствовать появлению интереса к математике у молодежи, как к самой перспективной науке.
Не все открытия в математике сделаны и не все теоремы доказаны.
Спешите их осталось еще 6!!!
3.2.Практическое применение работы
Моя работа может быть
Интересна учащимся увлеченным математикой.
Использована на факультативных занятиях.
Применена в работе математического кружка.
Наглядным материалом на уроках для активации познавательного интереса к математике у учащихся.
4.Литература.
Болтянский В.Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982.
Васильев В.А. Введение в топологию. — М.: ФАЗИС, 1997.
Вербицкий М. Лекции и задачи по топологии. — 2009.
Виро О.Я., Иванов О.А., Харламов В.М., Нецветаев,Н.Ю. Элементарная топология. — 2007.
Коснёвски Ч. Начальный курс алгебраической топологии. — М.: Мир, 1983.
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. — М.: Мир, 1972.
Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
Прасолов В.В. Наглядная топология. — М.: МЦНМО, 1995.
Стюарт Я. Топология. // Квант, № 7, 1992.
Топология, видео.
Интернет-ресурсы.
5.Приложение
Изготовлен информационный буклет.
infourok.ru