Доказательство гипотезы пуанкаре – Полное доказательство гипотезы Пуанкаре предъявлено уже тремя независимыми группами математиков

Содержание

Полное доказательство гипотезы Пуанкаре предъявлено уже тремя независимыми группами математиков

Три независимых группы математиков утверждают, что полностью доказали гипотезу Пуанкаре — одну из самых сложных задач XX века. Окончательный вердикт, возможно, будет вскоре объявлен на Международном конгрессе математиков.

Процесс доказательства гипотезы Пуанкаре сейчас, по-видимому, вступает в заключительную стадию. Три группы математиков окончательно разобрались в идеях Григория Перельмана и за последние пару месяцев представили свои версии полного доказательства этой гипотезы.

Гипотеза, сформулированная Пуанкаре в 1904 году, утверждает, что все трехмерные поверхности в четырехмерном пространстве, гомотопически эквивалентные сфере, гомеоморфны ей. Говоря простыми словами, если трехмерная поверхность кое в чем похожа на сферу, то, если ее расправить, она может стать только сферой и ничем иным. Подробности об этой гипотезе и об истории ее доказательства читайте в популярной заметке Проблемы 2000 года: гипотеза Пуанкаре в журнале «Компьютерра».

За доказательство гипотезы Пуанкаре Математический институт им. Клэя присудил премию в миллион долларов, что может показаться удивительным: ведь речь идет об очень частном, малоинтересном факте. На самом деле, для математиков важны не столько свойства трехмерной поверхности, сколько факт трудности самого доказательства. В этой задаче в концентрированном виде сформулировано то, что не удавалось доказать с помощью имевшихся ранее идей и методов геометрии и топологии. Она позволяет как бы заглянуть на уровень глубже, в тот пласт задач, который можно будет решить только с помощью идей «нового поколения».

Как и в ситуации с теоремой Ферма, выяснилось, что гипотеза Пуанкаре есть частный случай гораздо более общего утверждения о геометрических свойствах произвольных трехмерных поверхностей — гипотезы геометризации Тёрстона (Thurston’s Geometrization Conjecture). Поэтому усилия математиков были направлены не на решение этого частного случая, а на построение нового математического подхода, который способен справляться с такими задачами.

Прорыв в 2002-2003 годах совершил российский математик Григорий Перельман. В своих трех статьях math.DG/0211159, math.DG/0303109, math.DG/0307245, предложив ряд новых идей, он развил и довел до конца метод, предложенный в 1980-е годы Ричардом Гамильтоном. В своих работах Перельман утверждает, что построенная им теория позволяет доказать не только гипотезу Пуанкаре, но и гипотезу геометризации.

Суть метода состоит в том, что для геометрических объектов можно определить некоторое уравнение «плавной эволюции», похожее на уравнение ренормализационной группы в теорфизике. Исходная поверхность в ходе этой эволюции будет деформироваться и, как показал Перельман, в конце концов плавно перейдет именно в сферу. Сила этого подхода состоит в том, что, минуя все промежуточные моменты, можно сразу заглянуть «в бесконечность», в самый конец эволюции, и обнаружить там сферу.

Работы Перельмана положили начало интриге. В своих статьях он развил общую теорию и набросал ключевые моменты доказательства не только гипотезы Пуанкаре, но и гипотезы геометризации. Полного доказательства во всех деталях Перельман не представил, хотя утверждал, что обе гипотезы он доказал. В том же 2003 году Перельман совершил турне по США с серией лекций, на которых четко и подробно отвечал на любые технические вопросы слушателей.

Сразу же после опубликования препринтов Перельмана специалисты приступили к проверке ключевых моментов его теории, и ни одной ошибки до сих пор не найдено. Более того, за прошедшие годы несколько коллективов математиков смогли впитать предложенные Перельманом идеи до такой степени, чтобы приступить к записыванию полного доказательства «набело».

В мае 2006 года появилась работа B. Kleiner, J. Lott, math.DG/0605667, в которой был дан подробный вывод опущенных моментов в доказательстве Перельмана. (Кстати, эти авторы поддерживают веб-страничку, посвященную статьям Перельмана и связанным с ними работам.)

Затем в июне 2006 года в журнале Asian Journal of Mathematics была опубликована 327-страничная статья китайских математиков Huai-Dong Cao и Xi-Ping Zhu, озаглавленная «Полное доказательство гипотез Пуанкаре и геометризации — приложение теории Гамильтона—Перельмана о потоках Риччи». Сами авторы не претендуют на абсолютно новое доказательство, а лишь утверждают, что подход Перельмана действительно работает.

Наконец, на днях появился 473-страничная статья (или уже книга?) J. W. Morgan, G. Tian, math.DG/0607607, в которой авторы, по следам Перельмана, приводят свое доказательство гипотезы Пуанкаре (а не более общей гипотезы геометризации). Джон Морган (John Morgan) считается одним из главных специалистов по этой проблеме, и после выхода его работы можно, по-видимому считать, что гипотеза Пуанкаре окончательно доказана.

Интересно, кстати, что вначале статья китайских математиков распространялась только в бумажной версии по цене 69 долларов, так что далеко не все желающие имели возможность взглянуть на нее. Но уже на следующий день после появления в архиве препринтов статьи Моргана—Тяна на сайте

Asian Journal of Mathematics появилась и электронная версия статьи.

Чья доводка доказательства Перельмана точнее и прозрачнее — покажет время. Не исключено, что в ближайшие годы оно упростится, как это случилось с теоремой Ферма. Пока что видно лишь увеличение объема публикаций: от 30-страничных статей Перельмана до толстой книжицы у Моргана и Тяна, но связано это не с усложнением доказательства, а с более подробным выводом всех промежуточных шагов.

А тем временем ожидается, что на Международном конгрессе математиков, который пройдет в августе этого года в Мадриде, будет «официально» объявлено об окончательном доказательстве гипотезы и, возможно, о том, кому будет присуждена премия Института Клэя. Кроме этого, ходят слухи, что Григорий Перельман станет одним из четырех филдсовских медалистов, что является высшим знаком отличия для молодых математиков.

Игорь Иванов

elementy.ru

О гипотезе Пуанкаре. Лекция в Яндексе / Яндекс corporate blog / Habr

Еще в XIX веке было известно, что если любую замкнутую петлю, лежащую на двумерной поверхности, можно стянуть в одну точку, то такую поверхность легко превратить в сферу. Так, поверхность воздушного шарика удастся трансформировать в сферу, а поверхность бублика – нет (легко вообразить себе петлю, которая в случае с бубликом не стянется в одну точку). Гипотеза, высказанная французским математиком Анри Пуанкаре в 1904 году, гласит, что аналогичное утверждение верно и для трехмерных многообразий.

Доказать гипотезу Пуанкаре удалось только в 2003 году. Доказательство принадлежит нашему соотечественнику Григорию Перельману. Эта лекция проливает свет на объекты, необходимые для формулировки гипотезы, историю поиска доказательства и его основные идеи.

Читают лекцию доценты механико-математического факультета МГУ к. ф-м. н. Александр Жеглов и к. ф.-м. н. Федор Попеленский.

Если не вдаваться в математические подробности, то вопрос, поднимаемый гипотезой Пуанкаре можно следующим образом: как охарактеризовать (трехмерную) сферу? Чтобы правильно понять этот вопрос, нужно познакомиться с одним из важнейших понятий в топологии – гомеоморфизмом. Разобравшись с ним, мы сможем точно сформулировать гипотезу Пуанкаре.

Чтобы совсем уж не залезать в математические подробности формального определения, мы скажем, что две фигуры считаются гомеоморфными, если можно установить такое взаимно-однозначно соответствие между точками этих фигур, при котором близким точкам одной фигуры соответствуют близкие точки другой фигуры и наоборот. Пропущенные нами подробности состоят как раз в адекватной формализации близости точек.

Легко понять, что две фигуры гомеоморфны, если одну из другой можно получить произвольной деформацией, при которой запрещено «портить» поверхности (рвать, сминать области в точку, делать дырки и т.п.).

Например, чтобы получить из диска полусферу, как показано на картинке выше, нам потребуется просто нажать сверху в его центр, придерживая внешний обод. Можно представлять себе, что поверхности сделаны из идеальной резины, так что все фигуры могут сжиматься и растягиваться как угодно. Нельзя делать только две вещи: разрывать и склеивать.

Более точное (но все же не окончательное с точки зрения строгости) представление о гомеоморфных фигурах мы будем иметь, если разрешим еще одну операцию: можно сделать на фигуре разрез, перекрутить, завязать, развязать и т.п., но потом обязательно заклеить разрез как было.

Приведем еще один пример. Представим себе яблоко, в котором червяк прогрыз ход в виде узла и небольшую пещеру.

С точки зрения топологии поверхность этого яблока все равно останется сферой, т.к. если стянуть все это определенным образом, мы получим поверхность яблока в том же виде, как было до того, как червяк начал его есть.

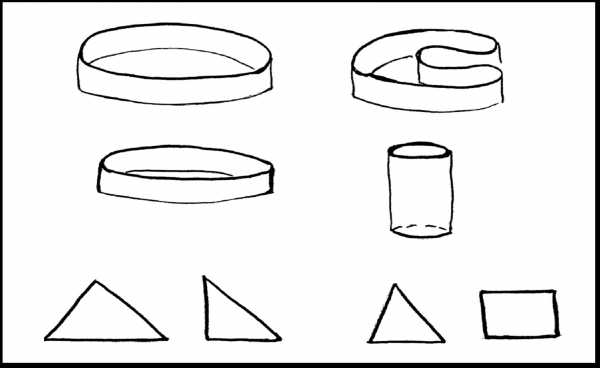
Для закрепления попробуйте классифицировать буквы латинского алфавита с точностью до гомеоморфизма (т.е. выясните, какие буквы гомеоморфны, а какие — нет). Ответ зависит начертания букв (от типа шрифта или от гарнитуры), и для простейшего варианта начертания он приведен на следующем рисунке:

Из 26 букв у нас получается всего 8 классов.

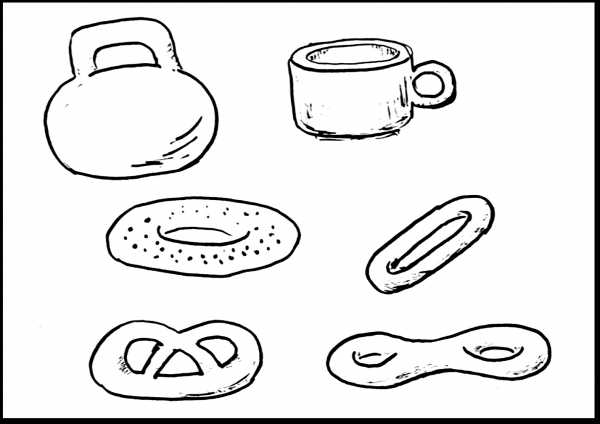
На следующей картинке изображены гиря, кофейная чашка, бублик, сушка и кренделек. С топологической точки зрения поверхности гири, кофейной чашки, бублика и сушки одинаковы, т.е. гомеоморфны. Что касается кренделька, то он приведен здесь для сравнения с поверхностью, которую в топологии часто называют кренделем (он изображен в правом нижнем углу рисунка). Как вы, наверное, уже понимаете, и топологический крендель, и съедобный крендель отличаются от тора.

Формальная постановка вопроса

Пусть M – замкнутое связное многообразие размерности 3. Пусть на нем любая петля может быть стянута в точку. Тогда M гомеоморфно трехмерной сфере.

Наибольшую трудность для неподготовленного человека здесь вызывает понятие «многообразия размерности 3» и свойства, выраженные словами «замкнутое» и «связное». Поэтому мы попробуем разобраться со всеми этими понятиями и свойствами на примере размерности 2, в этом случаем многое кардинально упрощается.

Гипотеза Пуанкаре для поверхностей

Пусть M – замкнутая связная поверхность (многообразие размерности 2). Пусть на ней любая петля может быть стянута в точку. Тогда поверхность M гомеоморфна двумерной сфере.

Сначала определим, что такое поверхность. Возьмем конечный набор многоугольников, разбиваем все их стороны (ребра) на пары (т.е. всего сторон у всех многоугольников должно быть четное число), в каждой паре выбираем, каким из двух возможных способов будем их склеивать. Склеиваем. В результате поучается замкнутая поверхность.

Если полученная поверхность состоит из одного куска, а не из нескольких отдельных, то говорят, что поверхность связна. С формальной точки зрения это значит, что после склейки из любой вершины любого многоугольника можно по ребрам пройти в любую другую вершину.

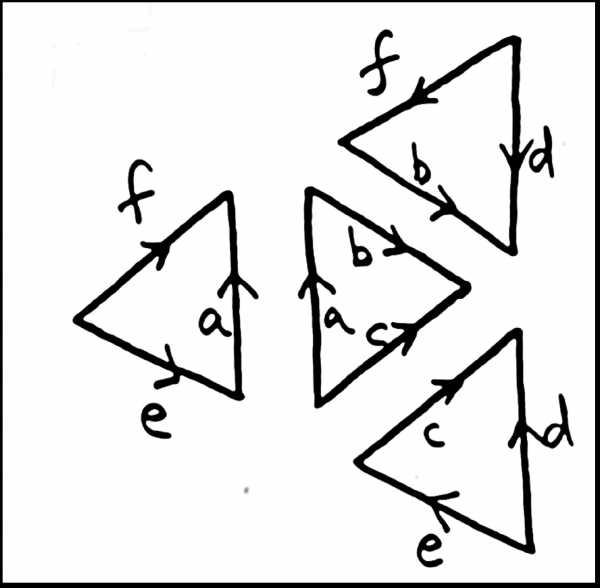
Вот простой пример: если считать, что на картинке выше все треугольники правильные, то после склеивания у нас должен получиться правильный тетраэдр, поверхность которого также гомеоморфна сфере.

Формально нужно требовать, чтобы из любой вершины любого многоугольника после склейки можно было пройти в любую вершину любого многоугольника (по ребрам).

Нетрудно сообразить, что связную поверхность можно склеить и из одного многоугольника. На рисунке видна идея, как это обосновывается:

Рассмотрим примеры простейших склеек:

В первом случае у нас получится сфера:

Во втором случае у нас получится тор (поверхность бублика, мы встречались с ним раньше):

В третьем случае получится так называемая бутылка Клейна:

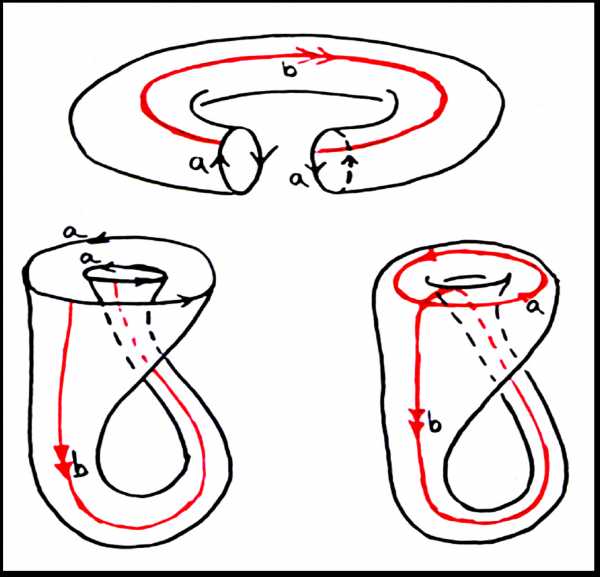
Если склеивать не все стороны многоугольника, то получится поверхность с краем:

Важно отметить, что после склейки «шрамы» от нее носят чисто «косметический характер. Все точки поверхности равноправны: у любой точки имеется окрестность гомеоморфная диску.

Две поверхности считаются гомеоморфными, если схемы склейки каждой из них можно так разрезать на схемы склейки из более мелких многоугольников, что схемы склейки станут одинаковыми.

Разберем это утверждение на примере разбиения поверхности куба на части, из которых можно сложить развертку тетраэдра:

Верен и более общий факт: поверхности всех выпуклых многогранников – это сферы.

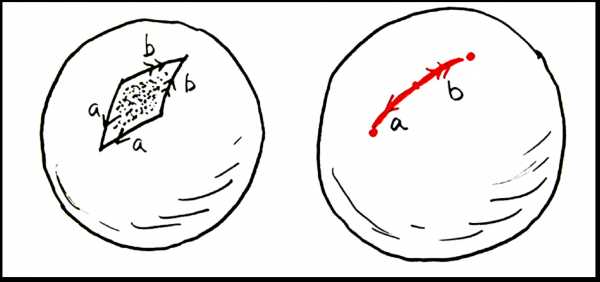
Теперь подробнее остановимся на понятии петли. Петял — это замкнутая кривая на рассматриваемой поверхности. Две петли называются гомотопными, если одну из них можно продеформировать в другую без разрывов и склеек, оставаясь на поверхности. Ниже приведен простейший случай стягивания петли на плоскости или сфере:

Даже если петля на плоскости или сфере имеет самопересечения, ее все равно можно стянуть:

На плоскости можно стянуть любую петлю:

А вот какие петли бывают на торе:

Стянуть такие петли невозможно. (К сожалению, доказательство выходит довольно далеко за рамки нашего рассказа.) Более того, показанные петли на торе не гомотопны. Предлагаем слушателям или читателям найти еще одну петлю на торе, не гомотопную этим двум — это очень простой вопрос. После этого попробуйте найти на торе четвертую петлю, не гомотопную этим трем — это будет несколько сложнее.

Эйлерова характеристика

Теперь, когда мы познакомились со всеми основными понятиями из формулировки гипотезы Пуанкаре, попробуем приступить к доказательству двумерного случая (лишний раз отметим, что это многократно проще трехмерного случая). А поможет нам в этом эйлерова характеристика.

Эйлеровой характеристикой поверхности M назовем число B−P+Г. Здесь Г — число многоугольников, Р — это число ребер после склейки (в случае рассматриваемых поверхностей это половина числа сторон всех многоугольников), B — это число вершин, которое получается после склейки после склейки.

Если две схемы склейки задают гомеоморфные поверхности, то у этих схем числа B−P+Г одинаковы, т. е. B−P+Г является инвариантом поверхности.

Если поверхность уже как-то задана, то надо нарисовать на ней какой-нибудь граф, чтобы после разрезания по нему поверхность распалась на куски гомеоморфные дискам (например, кольца запрещены). Затем подсчитываем величину B−P+Г — это и есть эйлерова характеристика поверхности.

Будут ли гомеоморфны поверхности с одинаковыми эйлеровыми характеристиками, мы узнаем позже. Но совершенно точно можно утверждать, что если эйлеровы характеристики у поверхностей разные, то поверхности не гомеоморфны.

Знаменитое соотношение B−P+Г=2 для выпуклых многоугольников (теорема Эйлера) является частным случаем этой теоремы. В данном случае речь идет о конкретной поверхности — о сфере. Замечание Обозначение: Эйлерову характеристику поверхности M будем обозначать через χ(M): χ(M) = B − P + Γ

Если поверхность M связна, то χ(M) ≤ 2, причем χ(M) = 2 тогда и только тогда, когда M гомеоморфна сфере.

Посмотрев лекцию до конца, вы узнаете, как же все-таки доказывается гипотеза Пуанкаре в размерности 2, и как Григорию Перельману удалось доказать ее в размерности 3.

habr.com

Теорема Пуанкаре простыми словами :: SYL.ru

Жюль Анри Пуанкаре (1854-1912) возглавлял Парижскую академию наук и был избран в научные академии 30 стран мира. Он имел масштаб Леонардо: его интересы охватывали физику, механику, астрономию, философию. Математики же всего мира до сих пор говорят, что только два человека в истории по-настоящему знали эту науку: немец Давид Гилберт (1862-1943) и Пуанкаре.

В 1904 году учёный опубликовал работу, содержавшую среди прочего предположение, получившее название теорема Пуанкаре. Поиск доказательства истинности этого утверждения занял около века.

Основатель топологии

Математический гений Пуанкаре впечатляет количеством разделов науки, где им были разработаны теоретические основы различных процессов и явлений. Во времена, когда ученые совершали прорывы в новые миры космоса и в глубины атома, было не обойтись без единой основы общей теории мироздания. Такой базой стали ранее неизвестные отрасли математики.

Пуанкаре искал новый взгляд на небесную механику, он создал качественную теорию дифференциальных уравнений, теорию автоморфных функций. Исследования ученого стали основой специальной теории относительности Эйнштейна. Теорема Пуанкаре о возвращении говорила среди прочего о том, что понять свойства глобальных объектов или явлений можно исследуя составляющие их частицы и элементы. Это дало мощный толчок научным поискам в физике, химии, астрономии и т.д.

Геометрия — отрасль математики, где Пуанкаре стал признанным новатором и лидером мирового масштаба. Теория Лобачевского, открыв новые измерения и пространства, еще нуждалась в ясной и логичной модели, и Пуанкаре придал идеям великого русского ученого прикладной характер.

Развитием неэвклидовой геометрии стало возникновение топологии – отрасли математики, которую называли геометрией размещения. Она изучает пространственные взаимоотношения точек, линий, плоскостей, тел и т.д. без учета их метрических свойств. Теорема Пуанкаре, ставшая символом самых трудноразрешимых задач в науке, возникла именно в недрах топологии.

Одна из семи задач тысячелетия

В самом начале XXI века одно из подразделений американского университета в Кембридже — математический институт, основанный на средства бизнесмена Лэндона Т. Клэя — опубликовал список Millennium Prize Problems (проблем тысячелетия). Он содержал семь пунктов из классических научных задач, за решение каждой из которых учреждалась премия в миллион долларов:

• Равенство классов P и NP (о соответствии алгоритмов решения задачи и методов проверки их правильности).
• Гипотеза Ходжа (о связи объектов и их подобия, составленного для их изучения из «кирпичиков» с определенными свойствами).
• Гипотеза Пуанкаре (всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере).
• Гипотеза Римана (о закономерности размещения простых чисел).
• Теория Янга — Миллса (уравнения из области элементарных частиц, описывающие различные виды взаимодействий).
• Существование и гладкость решений уравнений Навье — Стокса (описывают турбулентность течений воздуха и жидкостей).
• Гипотеза Бёрча — Свиннертон-Дайера (об уравнениях, описывающих эллиптические кривые).

Каждая эта проблема имела очень долгую историю, поиски их решения приводили к возникновению целых новых научных направлений, но единственно правильные ответы на поставленные вопросы не находились. Понимающие люди говорили, что деньги фонда Клэя в безопасности, но так было лишь до 2002 года – появился тот, кто доказал теорему Пуанкаре. Правда, деньги он не взял.

Классическая формулировка

Гипотеза, для которой найдено подтверждение, становится теоремой, имеющей корректное доказательство. Именно это произошло с высказанным Пуанкаре предположением о свойствах трехмерных сфер. В более общем виде этот постулат говорил о гомеоморфности всякого многообразия размерности n и сферы размерности n как необходимом условии их гомотопической эквивалентности. Знаменитая теперь теорема Пуанкаре относится к варианту, когда n=3. Именно в трехмерном пространстве математиков ждали затруднения, для других случаев доказательства были найдены быстрее.

Чтобы хоть немного постичь смысл теоремы Пуанкаре, не обойтись без знакомства с основными понятиями топологии.

Гомеоморфизм

Топология, говоря о гомеоморфизме, определяет его как взаимно-однозначное соответствие между точками одной и другой фигуры, в некотором смысле неотличимость. Неподготовленному сложно даётся теорема Пуанкаре. Для чайников можно привести самый популярный пример гомеоморфных фигур – шар и куб, также гомеоморфны бублик и кружка, но не кружка и куб. Фигуры гомеоморфны, если одну фигуру можно получить произвольной деформацией из другой, причем это преобразование ограничено некоторыми свойствами поверхности фигуры: её нельзя рвать, прокалывать, разрезать.

Если куб раздуть, он легко может стать шаром, если шар примять встречными движениями, можно получить кубик. Наличие дырки у бублика и дырки, образованной ручкой у кружки, делает их гомеоморфными, та же дырка делает невозможным превращение кружки в шар или куб.

Связность

Дырка – важное понятие, определяющее свойства объекта, но категория совершенно не математическая. Было введено понятие связности. Его содержат многие топологические постулаты, в том числе и теорема Пуанкаре. Простыми словами можно говорить так: если поверхность шара обернуть петлей из резиновой ленты, она, сжимаясь, соскользнёт. Этого не произойдет, если имеется отверстие, как у тора-бублика, сквозь которое можно продеть эту ленту. Таким образом определяется главный признак сходства или отличия объектов.

Многообразие

Если объект или пространство разделить на множество составных частей – окрестностей, окружающих какую-то точку, — то их общность называют многообразием. Именно такое понятие содержит теорема Пуанкаре. Компактность означает конечное число элементов. Каждая отдельная окрестность подчиняется законам традиционной – эвклидовой – геометрии, но вместе они образуют нечто более сложное.

Самая адекватная аналогия этих категорий – поверхность земли. Изображение её поверхности представляет собой карты отдельных её районов, собранные в атлас. На глобусе эти изображения обретают форму шара, который относительно пространства Вселенной превращается в точку.

Трехмерная сфера

По определению, сфера – совокупность точек, которые равноудалены от центра – некой фиксированной точки. Одномерная сфера расположена в двухмерном пространстве в виде окружности на плоскости. Двухмерная сфера – поверхность шара, его «корочка» — совокупность точек в трехмерном пространстве и, соответственно, трехмерная сфера – суть теоремы Пуанкаре – поверхность четырехмерного шара. Вообразить такой объект очень трудно, но, говорят, мы — внутри такого геометрического тела.

Математики приводят ещё и такое описание трехмерной сферы: допустим, что к нашему привычному пространству, считаемому неограниченным и определяемому тремя координатами (X, Y, Z), добавлена точка (на бесконечности) таким образом, что в неё всегда можно попасть, двигаясь в любом направлении по прямой линии, т.е. любая прямая в этом пространстве становится окружностью. Говорят, что есть люди, которые могут это вообразить и спокойно ориентироваться в таком мире.

Для них обычное дело – трехмерный тор. Такой объект можно получить путем дважды повторенного совмещения в одну точку двух, расположенных на противоположных (например, правой и левой, верхней и нижней) гранях куба. Чтобы попытаться представить трехмерный тор с привычных нам позиций, следует провести абсолютно нереальный эксперимент: необходимо выбрать направления, взаимно перпендикулярные, – вверх, влево и вперед – и начать двигаться в любом из них по прямой. Через какое-то (конечное) время с противоположного направления мы вернемся в исходную точку.

Такое геометрическое тело имеет принципиальное значение, если хотеть понять, что такое теорема Пуанкаре. Доказательство Перельмана сводится к обоснованию существования в трехмерном пространстве лишь одного односвязного компактного многообразия – 3-сферы, другие, как 3-тор, неодносвязные.

Долгий путь к истине

Прошло более полувека, прежде чем появилось решение теоремы Пуанкаре для больших чем 3 размерностей. Стивен Смэйл (род. 1930), Джон Роберт Стэллингс (1935-2008), Эрик Кристофер Зиман (род. 1925) нашли решение для n, равного 5, 6 и равного или больше 7. Только в 1982 году Майкл Фридман (род. 1951) был удостоен высшей математической награды – Филдсовской премии – за доказательство теоремы Пуанкаре для более сложного случая: когда n=4.

В 2006 году эта награда — медаль Филдса — была присвоена русскому математику из Санкт-Петербурга. Григорий Яковлевич Перельман доказал теорему Пуанкаре для трехмерного многообразия и трёхмерной сферы. Получать награду он отказался.

Обыкновенный гений

Григорий Яковлевич родился 13 июня в Ленинграде, в интеллигентной семье. Отец — инженер-электрик — в начале 90-х уехал на ПМЖ в Израиль, мать преподавала математику в ПТУ. Кроме любви к хорошей музыке, она привила сыну увлечение решением задач и головоломок. В 9-м классе Григорий перевелся в физико-математическую школу № 239, но еще с 5-го класса он посещал математический центр при Дворце пионеров. Победы во всесоюзных и международных олимпиадах позволили поступить Перельману в Ленинградский университет без экзаменов.

Многие специалисты, особенно российские, отмечают что Григорий Яковлевич был подготовлен к невиданному взлету высоким классом ленинградской школы геометров, какую он прошел на мехмате Ленинградского госуниверситета и в аспирантуре при Математическом институте им. В.А. Стеклова. Став кандидатом наук, он стал работать в нем.

Трудное время 90-х заставило молодого ученого уехать на работу в США. Те, кто знал его тогда, отмечали его аскетизм в быту, увлечённость работой, прекрасную подготовку и высокую эрудицию, которые и стали залогом того, что Перельман доказал теорему Пуанкаре. Вплотную он занялся этой проблемой после возвращения в Санкт-Петербург в 1996 году, но начал думать над ней еще в США.

Верное направление

Григорий Яковлевич отмечает, что его всегда увлекали сложные проблемы, такие как теорема Пуанкаре. Доказательство Перельман стал искать в направлении, вынесенном из беседы с профессором Колумбийского университета Ричардом Гамильтоном (род. 1943). Во время пребывания в США он специально ездил из другого города на лекции этого неординарного ученого. Перельман отмечает прекрасное доброжелательное отношение профессора к молодому математику из России. В их разговоре Гамильтон упомянул о потоках Риччи – системе дифференциальных уравнений – как способе решения теорем геометризации.

Впоследствии Перельман пытался связаться с Гамильтоном и обсудить ход работы над задачей, но не получил ответа. Долгое время после возвращения на родину Григорий Яковлевич провел наедине с труднейшей задачей, которой была теорема Пуанкаре. Доказательство Перельмана – итог огромных усилий и самоотречения.

Гамильтон пришел в тупик, когда увидел, что при преобразованиях кривых под действием потоков Риччи образуются сингулярные (обращающиеся в бесконечность) зоны, которые не предусматривала теорема Пуанкаре. Простыми словами, Перельману удалось нейтрализовать образование таких зон, и многообразие благополучно превратилось в сферу.

Потоки Риччи

Односвязное 3-мерное многообразие наделяется геометрией, вводятся метрические элементы с расстоянием и углами. Легче понять это на одномерных многообразиях. Гладкая замкнутая кривая на эвклидовой плоскости наделяется в каждой точке касательным вектором единичной длины. При обходе кривой вектор поворачивается с определенной угловой скоростью, которая определяет кривизну. Где линия изогнута сильнее, кривизна больше. Кривизна положительна, если вектор скорости повернут в сторону внутренней части плоскости, которую делит наша линия, и отрицательна, если повернут вовне. В местах перегиба кривизна равна 0.

Теперь каждой точке кривой назначается вектор, перпендикулярный вектору угловой скорости, а длиной равный величине кривизны. Его направление внутрь при положительной кривизне и вовне — при отрицательной. Каждую точку заставляем двигаться в направлении и со скоростью, определяемыми соответствующим вектором. Замкнутая кривая, проведенная в любом месте плоскости, при такой эволюции превращается в окружность. Это справедливо для размерности 3, что и требовалось доказать.

Нет пророка…

Он взошел на свой Эверест, каким признается математиками теорема Пуанкаре. Доказательство Перельман выложил в Интернет в виде трех небольших статей. Они немедленно вызвали ажиотаж, хотя русский математик не пошел положенной дорогой – публикация в специализированном журнале в сопровождении профессиональных рецензий. Григорий Яковлевич в течение месяца разъяснял в университетах США суть своего открытия, но число до конца понявших ход его мысли увеличивалось очень медленно.

Лишь через четыре года появилось заключение самых больших авторитетов: доказательства русского математика корректны, первая из проблем тысячелетия решена.

Эпоха соцсетей

Ему пришлось пережить ажиотаж и хамство в соцсетях, молчание тех, кого он уважал, и крики других, учивших его жизни. Энергичные китайцы сначала оценили его вклад в решение проблемы в 25 %, себе и другим насчитав 80! Потом вроде бы пришло мировое признание, но выдержать такое дано не каждому.

Хочется верить: он выдержал, и в жизни его — гармония желаний и возможностей.

www.syl.ru

«Я знаю, как управлять Вселенной».

Главная
2011
Май
Григорий Перельман: «Я знаю, как управлять Вселенной».

«Зачем мне миллион?»

На весь мир известна история про гениального математика Григория Перельмана, доказавшего гипотезу Пуанкаре, который отказался от миллиона долларов. Недавно учёный-затворник объяснил, наконец, почему же он не взял заслуженную премию.

Началось всё с того, что журналист и продюсер кинокомпании «Президент-фильм» Александр Забровский догадался связаться с матерью Григория Яковлевича через еврейскую общину Петербурга. Ведь до этого все журналисты безрезультатно просиживали штаны на ступенях дома великого математика с целью взять у него интервью. Мать поговорила с сыном, дав журналисту хорошую характеристику, и только после этого Перельман согласился на встречу.

По словам Забровского, Григорий Яковлевич – вполне вменяемый и адекватный человек, а всё, что о нём говорили ранее – бред сивой кобылы. Он видит перед собой конкретную цель и знает, как к ней прийти.

Кинокомпания «Президент-фильм» с согласия Перельмана планирует снять о нем художественную ленту «Формула Вселенной». Математик и пошёл-то на контакт ради этого фильма, который будет не о нём, а о сотрудничестве и противоборстве трех основных мировых математических школ: российской, китайской и американской, наиболее продвинувшихся по стезе изучения и управления Вселенной. На вопрос о миллионе, который так волновал всех удивлённых и любопытных, Перельман ответил: «Я знаю, как управлять Вселенной. И скажите – зачем же мне бежать за миллионом?»

Учёный рассказал и про то, почему он не общается с журналистами. Причина в том, что их волнует не наука, а личная жизнь – стрижка ногтей и миллион. Его обижает, когда в прессе его называют Гришей, такую фамильярность математик считает неуважением к себе.

Со школьных лет Григорий Перельман привык «тренировать мозг», то есть решать задачи, которые заставляли мыслить абстрактно. И чтобы найти правильно решение, нужно было представить себе «кусочек мира». Например, математику предложили посчитать, с какой скоростью должен был идти Иисус Христос по воде, чтобы не провалиться. Оттуда и пошло желание Перельмана изучать свойства трехмерного пространства Вселенной.

Для чего же надо было столько лет биться над доказательством гипотезы Пуанкаре? Суть её такова: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу. «Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной.

Григорий Яковлевич постиг таких сверхзнаний, которые помогают понять мироздание. И теперь математик постоянно под наблюдением российских и зарубежных спецслужб: а вдруг Перельман представляет угрозу для человечества? Ведь если с помощью его знаний можно свернуть Вселенную в точку, а потом ее развернуть, то мы можем погибнуть либо возродиться в ином качестве? И тогда мы ли это будем? И нужно ли нам вообще управлять Вселенной?

Доказательство длиною в век

Григорий Перельман окончательно и бесповоротно вошел в историю

Математический институт Клэя присудил Григорию Перельману Премию тысячелетия (Millennium Prize), тем самым официально признав верным доказательство гипотезы Пуанкаре, выполненное российским математиком. Примечательно, что при этом институту пришлось нарушить собственные правила — по ним на получение примерно миллиона долларов, именно таков размер премии, может претендовать только автор, опубликовавший свои работы в рецензируемых журналах. Работа Григория Перельмана формально так и не увидела свет — она осталась набором нескольких препринтов на сайте arXiv.org (один, два и три). Впрочем, не так важно, что стало причиной решения института — присуждение Премии тысячелетия ставит точку в истории длиной более чем в 100 лет.

Кружка, пончик и немного топологии

Прежде чем выяснить, в чем состоит гипотеза Пуанкаре, необходимо разобраться, что это за раздел математики — топология, — к которому эта самая гипотеза относится. Топология многообразий занимается свойствами поверхностей, которые не меняются при определенных деформациях. Поясним на классическом примере. Предположим, что перед читателем лежит пончик и стоит пустая чашка. С точки зрения геометрии и здравого смысла — это разные объекты хотя бы потому, что попить кофе из пончика не получится при всем желании.

Однако тополог скажет, что чашка и пончик — это одно и то же. И объяснит это так: вообразим, что чашка и пончик представляют собой полые внутри поверхности, изготовленные из очень эластичного материала (математик бы сказал, что имеется пара компактных двумерных многообразий). Проведем умозрительный эксперимент: сначала раздуем дно чашки, а потом ее ручку, после чего она превратится в тор (именно так математически называется форма пончика). Посмотреть, как примерно выглядит этот процесс можно.

Разумеется, у пытливого читателя возникает вопрос: раз поверхности можно мять, то как же их различать? Ведь, например, интуитивно понятно — как ни мни тор, без разрывов и склеек сферу из него не получишь. Тут в игру вступают так называемые инварианты — характеристики поверхности, которые не меняются при деформации, — понятие, необходимое для формулировки гипотезы Пуанкаре.

Здравый смысл подсказывает нам, что тор от сферы отличает дырка. Однако дырка — понятие далеко не математическое, поэтому его надо формализовать. Делается это так — представим, что на поверхности у нас имеется очень тонкая эластичная нить, образующая петлю (саму поверхность в этом умозрительном опыте, в отличие от предыдущего, считаем твердой). Будем двигать петлю, не отрывая ее от поверхности и не разрывая. Если нить можно стянуть до очень маленького кружочка (почти точки), то говорят, что петля стягиваема. В противном случае петля называется нестягиваемой.

Так вот, легко видеть, что на сфере любая петля стягиваема (как это примерно выглядит, можно посмотреть), а вот для тора это уже не так: на бублике есть целых две петли — одна продета в дырку, а другая обходит дырку «по периметру», - которые нельзя стянуть.

На этой картинке примеры нестягиваемых петель показаны красным и фиолетовым цветом соответственно. Когда на поверхности есть петли, математики говорят, что «фундаментальная группа многообразия нетривиальна», а если таких петель нет — то тривиальна.

Фундаментальная группа тора обозначается п1 (T2). Из-за того, что она нетривиальна, руки мыши образуют нестягиваемую петлю. Грусть на лице животного — результат осознания этого факта.

Так вот, легко видеть, что на сфере любая петля стягиваема, а вот для тора это уже не так: на бублике есть целых две петли — одна продета в дырку, а другая обходит дырку «по периметру», — которые нельзя стянуть. На этой картинке примеры нестягиваемых петель показаны красным и фиолетовым цветом соответственно.

Теперь, чтобы честно сформулировать гипотезу Пуанкаре, любознательному читателю осталось потерпеть еще немного: надо разобраться, что такое трехмерное многообразие в общем и трехмерная сфера в частности.

Вернемся на секундочку к поверхностям, которые мы обсуждали выше. Каждую из них можно разрезать на такие мелкие кусочки, что каждый будет почти напоминать кусочек плоскости. Так как у плоскости всего два измерения, то говорят, что и многообразие двумерно. Трехмерное многообразие — это такая поверхность, которую можно разрезать на мелкие кусочки, каждый из которых очень похож на кусочек обычного трехмерного пространства.

Главным «действующим лицом» гипотезы является трехмерная сфера. Представить себе трехмерную сферу как аналог обычной сферы в четырехмерном пространстве, не потеряв при этом рассудок, все-таки, наверное, невозможно. Однако описать этот объект, так сказать, «по частям» достаточно легко. Все, кто видел глобус, знают, что обычную сферу можно склеить из северного и южного полушария по экватору. Так вот, трехмерная сфера склеивается из двух шаров (северного и южного) по сфере, которая представляет собой аналог экватора.

На трехмерных многообразиях можно рассмотреть такие же петли, какие мы брали на обычных поверхностях. Так вот, гипотеза Пуанкаре утверждает: «Если фундаментальная группа трехмерного многообразия тривиальна, то оно гомеоморфно сфере». Непонятное словосочетание «гомеоморфно сфере» в переводе на неформальный язык означает, что поверхность можно продеформировать в сферу.

В 1887 году Пуанкаре представил работу на математический конкурс, посвященный 60-летию короля Швеции Оскара II. В ней обнаружилась ошибка, которая привела к появлению теории хаоса.

Немного истории

Вообще говоря, в математике можно сформулировать большое количество сложных утверждений. Однако что делает ту или иную гипотезу великой, отличает ее от остальных? Как это ни странно, но великую гипотезу отличает большое количество неправильных доказательств, в каждом из которых есть по великой ошибке — неточности, которая зачастую приводит к возникновению целого нового раздела математики.

Так, изначально Анри Пуанкаре, который отличался помимо всего прочего умением совершать гениальные ошибки, сформулировал гипотезу немного в другом виде, чем мы написали выше. Спустя некоторое время он привел контрпример к своему утверждению, который стал известен как гомологическая 3-сфера Пуанкаре, и в 1904 году сформулировал гипотезу уже в современном виде. Сферу, кстати, совсем недавно ученые приспособили в астрофизике — оказалось, что Вселенная вполне может оказаться гомологической 3-сферой Пуанкаре.

Надо сказать, что особого ажиотажа среди коллег-геометров гипотеза не вызвала. Так было до 1934 года, когда британский математик Джон Генри Уайтхед представил свой вариант доказательства гипотезы. Очень скоро, однако, он сам нашел в рассуждениях ошибку, которая позже привела к возникновению целой теории многообразий Уайтхеда.

После этого за гипотезой постепенно закрепилась слава крайне сложной задачи. Многие великие математики пытались взять ее приступом. Например, американский Эр Аш Бинг (R.H.Bing), математик, у которого (абсолютно официально) вместо имени в документах были записаны инициалы. Он предпринял несколько безуспешных попыток доказать гипотезу, сформулировав в ходе этого процесса собственное утверждение — так называемую «гипотезу о свойстве П» (Property P conjecture). Примечательно, что это утверждение, которое рассматривалось Бингом как промежуточное, оказалось чуть ли не сложнее доказательства самой гипотезы Пуанкаре.

Были среди ученых и люди, положившие жизнь на доказательство этого математического факта. Например, известный математик греческого происхождения Кристос Папакириакопоулос. В течение более десяти лет, Примечательно, что обобщение гипотезы Пуанкаре на многообразия размерности выше трех оказалось заметно проще оригинала — лишние размерности позволяли легче манипулировать многообразиями. Так, для n-мерных многообразий (при n не меньше 5) гипотеза была доказана Стивеном Смейлом в 1961 году. Для n = 4 гипотеза была доказана методом, совершенно отличным от смейловского, в 1982 году Майклом Фридманом. За свое доказательство последний получил Филдсовскую медаль — высшую награду для математиков. Работая в Принстоне, он безуспешно пытался доказать гипотезу. Он умер от рака в 1976 году. Примечательно, что обобщение гипотезы Пуанкаре на многообразия размерности выше трех оказалось заметно проще оригинала — лишние размерности позволяли легче манипулировать многообразиями. Так, для n-мерных многообразий (при n не меньше 5) гипотеза была доказана Стивеном Смейлом в 1961 году. Для n = 4 гипотеза была доказана методом, совершенно отличным от смейловского, в 1982 году Майклом Фридманом.
Описанные работы — это далеко не полный список попыток решения более чем столетней гипотезы. И хотя каждая из работ и привела к возникновению целого направления в математике и может считаться в этом смысле успешной и значимой, доказать гипотезу Пуанкаре окончательно удалось только россиянину Григорию Перельману.

Перельман и доказательство

В 1992 году Григорий Перельман, тогда сотрудник математического института им. Стеклова, попал на лекцию Ричарда Гамильтона. Американский математик рассказывал о потоках Риччи — новом инструменте для изучения гипотезы геометризации Терстона — факта, из которого гипотеза Пуанкаре получалась как простое следствие. Эти потоки, построенные в некотором смысле по аналогии с уравнениями теплопереноса, заставляли поверхности с течением времени деформироваться примерно так же, как в начале этой статьи мы деформировали двумерные поверхности. Оказалось, что в некоторых случаях результатом такой деформации оказывался объект, структуру которого легко понять. Основная трудность заключалась в том, что во время деформации возникали особенности с бесконечной кривизной, аналогичные в некотором смысле черным дырам в астрофизике.

После лекции Перельман подошел к Гамильтону. Позже он рассказывал, что Ричард его приятно удивил: «Он улыбался и был очень терпелив. Он даже рассказал мне несколько фактов, которые были опубликованы спустя лишь несколько лет. Он сделал это без колебаний. Его открытость и доброта поразили меня. Не могу сказать, что большинство современных математиков ведет себя так.»

После поездки в США Перельман вернулся в Россию, где принялся трудиться над решением проблемы особенностей потоков Риччи и доказательством гипотезы геометризации (а вовсе не над гипотезой Пуанкаре) втайне от всех. Ничего удивительного, что появление 11 ноября 2002 года первого препринта Перельмана повергло математическую общественность в шок. Спустя некоторое время появилась еще пара работ.

После этого Перельман самоустранился от обсуждения доказательств и даже, говорят, прекратил заниматься математикой. Он не прервал своего уединенного образа жизни даже в 2006 году, когда ему была присуждена Филдсовская премия — самая престижная награда для математиков. Причины такого поведения автора обсуждать не имеет смысла — гений имеет право вести себя странно (например, будучи в Америке Перельман не стриг ногти, позволяя им свободно расти).

Как бы то ни было, доказательство Перельмана зажило
отдельной от него жизнью: три препринта не давали покоя математикам современности. Первые результаты проверки идей российского математика появились в 2006 году — крупные геометры Брюс Кляйнер и Джон Лотт из Мичиганского университета опубликовали препринт собственной работы, по размерам больше напоминающей книгу — 213 страниц. В этой работе ученые тщательно проверили все выкладки Перельмана, подробно пояснив различные утверждения, которые в работе российского математика были лишь вскользь обозначены. Вердикт исследователей был однозначен: доказательство абсолютно верное.

Неожиданный поворот в этой истории наступил в июле этого же года. В журнале Asian Journal of Mathematics появилась статья китайских математиков Сипин Чжу и Хуайдун Цао под названием «Полное доказательство гипотезы геометризации Терстона и гипотезы Пуанкаре». В рамках этой работы результаты Перельмана рассматривались как важные, полезные, но исключительно промежуточные. Данная работа вызвала удивление у специалистов на Западе, однако получила очень одобрительные отзывы на Востоке. В частности, результаты поддержал Шинтан Яу — один из основоположников теории Калаби-Яу, положившей начало теории струн, — а также учитель Цао и Джу. По счастливому стечению обстоятельств именно Яу был главным редактором журнала Asian Journal of Mathematics, в котором была опубликована работа.

После этого математик стал ездить по миру с популярными лекциями, рассказывая о достижениях китайских математиков. В результате возникла опасность, что очень скоро результаты Перельмана и даже Гамильтона окажутся отодвинуты на второй план. Такое в истории математики случалось не раз — многие теоремы, носящие имена конкретных математиков, были придуманы совершенно другими людьми.

Однако этого не случилось и, вероятно, теперь не случится. Вручение премии Клэя Перельману (даже если тот откажется) навсегда закрепило в общественном сознании факт: российский математик Григорий Перельман доказал гипотезу Пуанкаре. И неважно, что на самом деле он доказал факт более общий, развив по пути совершенно новую теорию особенностей потоков Риччи. Хотя бы так. Награда нашла героя.
Андрей Коняев

Автор: Татьяна Шевченко

Подготовил: Сергей Коваль

Источник: http://eterra.info/news/

Дата публикации:

история проблемы, доказательство, смысл :: SYL.ru

По школьному курсу каждый знаком с понятиями теоремы и гипотезы. Как правило, в жизни затрагиваются самые простые и примитивные законы, в то время как математики делают очень сложные предположения и ставят интересные проблемы. Далеко не всегда им самим удается найти решения и доказательства, а в некоторых случаях над этим многие годы бьются их последователи и просто коллеги.

Институт Клея в 2000 году сформировал список из 7 так называемых Проблем Тысячелетия по аналогии с перечнем гипотез, составленным в 1900 году. Те задачи почти все оказались к настоящему времени решены, только одна из них перекочевала в обновленную версию. Сейчас список проблем выглядит следующим образом:

гипотеза Ходжа;
равенство классов P и NP;
гипотеза Пуанкаре;
теория Янга-Миллса;
гипотеза Римана;
существование и гладкость решения уравнений Навье-Стокса;
гипотеза Берча-Свиннертон-Дайера.

Все они относятся к различным дисциплинам внутри математики и имеют важное значение. Например, уравнения Навье-Стокса относятся к гидродинамике, а на практике могут описать поведение вещества в земной магме или пригодиться в предсказании погоды. Но все эти проблемы все еще ищут своего доказательства или опровержения. Кроме одной.

Теорема Пуанкаре

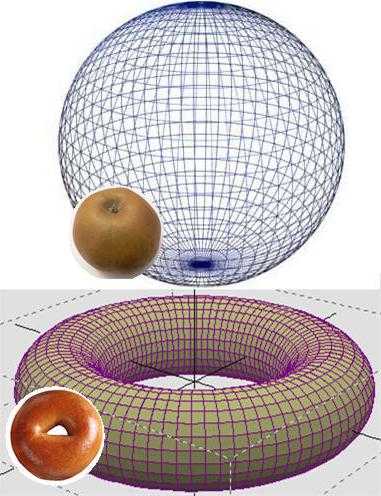
Объяснить простыми словами, в чем заключается эта проблема, довольно непросто, но попробовать можно. Представим себе сферу, к примеру, мыльный пузырь. Все точки его поверхности равноудалены от его центра, который ей не принадлежит. Но это двумерное тело, а гипотеза говорит о трехмерном. Это представить уже невозможно, но на то у нас и есть теоретическая математика. При этом, разумеется, все точки этого тела также будут удалены от центра.

Эта проблема относится к топологии — науке о свойствах геометрических фигур. И одним из базовых терминов в ней является гомеоморфность, то есть высокая степень схожести. Чтобы привести пример, можно представить шар и тор. Одну фигуру никак нельзя получить из другой, избежав разрывов, а вот конус, куб или цилиндр из первого получатся довольно легко. Вот гипотеза Пуанкаре и посвящена этим метаморфозам с одной лишь разницей — речь идет о многомерном пространстве и телах.

История

Французский математик Анри Пуанкаре занимался самыми разными областями науки. О его достижениях может сказать, к примеру, тот факт, что совершенно независимо от Альберта Эйнштейна он выдвинул основные положения специальной теории относительности. В 1904 году он поднял проблему доказательства того, что любое трехмерное тело, обладающее некоторыми свойствами сферы, ею и является с точностью до деформации. Позднее она была расширена и обобщена, и стала частным случаем гипотезы Терстона, сформулированной в 1982 году.

Формулировка

Пуанкаре изначально оставил такое утверждение: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. В дальнейшем оно было расширено и обобщено. И все же на протяжении длительного времени именно изначальная задача вызывала больше всего проблем, и была решена лишь через 100 лет после ее появления.

Интерпретация и смысл

О том, что такое гомеоморфность, речь уже шла. Теперь стоит поговорить о компактности и односвязности. Первое означает лишь, что многообразие имеет ограниченные размеры, не может быть непрерывно и бесконечно растянуто.

Что касается односвязаности, можно попробовать привести простой пример. Двумерная сфера — яблоко — обладает одним интересным свойством. Если взять обычную замкнутую резинку и приложить ее к поверхности, то плавной деформацией ее можно свести в одну точку. Это и есть свойство односвязаности, но представить его применительно к трехмерному пространству довольно затруднительно.

Если говорить совсем просто, проблематика заключалась в том, чтобы доказать, что односвязность — уникальное для сферы свойство. И если, условно говоря, опыт с резинкой завершился с таким результатом, то тело гомеоморфно ей. Что же касается приложения этой теории к жизни, Пуанкаре считал, что Вселенная в некотором смысле и является трехмерной сферой.

Доказательство

Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.

В 1930-х годах интерес к гипотезе вернулся. Прежде всего, формулировка была расширена до «n-мерного пространства», а потом американец Уайтхед сообщил об успешном доказательстве, позднее отказавшись от него. В 60-70-х сразу два математика — Смейл и Столлингс — практически одновременно, но разными способами разработали решение для всех n больше 4.

В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.

Дальше работа несколько застопорилась — американец Ричард Гамильтон предложил использовать в решении поток Риччи, но столкнулся с трудностями и не завершил исследования.

На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили «до блеска» американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.

Признание и оценки

Разумеется, это сразу стало сенсацией, ведь решение одной из Проблем Тысячелетия просто не могло оказаться незамеченным. Еще больше удивления вызывал тот факт, что Григорий Перельман отказался от всех наград и премий, сообщив, что ему и так прекрасно живется. В умах обывателей он сразу стал примером того самого полусумасшедшего гения, которого интересует только наука.

Все это вызвало много обсуждений в прессе и СМИ, что популярность математика стала его тяготить. Летом 2014 года прошла информация о том, что Перельман уехал работать в Швецию, но это оказалось лишь слухами, он все еще скромно живет в Санкт-Петербурге и почти ни с кем не общается. Среди наград, присужденных ему, были не только премия института Клея, но и престижная медаль Филдса, но он отказался от всего. Впрочем, Гамильтон, который по оценкам Перельмана сделал не меньший вклад в доказательство, тоже не был забыт. В 2009 и 2011 годах он также удостоился некоторых престижных наград и премий.

Отражение в культуре

Несмотря на то что для простых обывателей как постановка, так и решение этой проблемы представляют мало смысла, о доказательстве стало известно довольно быстро. В 2008 году по этому поводу японским режиссером Масахито Касуга был снят документальный фильм «Чары гипотезы Пуанкаре», посвященный столетним попыткам решить эту задачу.

В съемках приняли участие многие математики, занимавшиеся этой проблемой, но вот главный герой — Григорий Перельман — сделать этого не захотел. Более или менее близкие его знакомые также были задействованы в съемках. Документальный фильм, выйдя на экраны на волне общественного резонанса по поводу отказа ученого принять премию, в определенных кругах снискал славу, а также получил несколько наград. Что же касается массовой культуры, простые люди до сих пор гадают, какими доводами руководствовался петербургский математик, отказавшись взять деньги, когда он мог отдать их, например, на благотворительность.

www.syl.ru

Что же доказал Григорий Перельман? — Троицкий вариант — Наука

Фото Н. ЧетвериковойПоследним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002—2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S³».

В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).

Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.

Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией:Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).

Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы.

1. Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R³, а также любые открытые множества точек в R³, к примеру внутренность полнотория (бублика). Если рассмотреть замкнутое полно-торие, т. е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем -у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.

2. Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, что-то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы.

3. Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R³ односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.

4. Компактное. Многообразие компактно, если любой его гомео-морфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.

Размерность многообразия -это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т. е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т. д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна.

Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий — ведь у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка.

Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые¹многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности.

¹За неимением места, я не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна — поверхность, которую нельзя вложить в пространство без самопересечений.

На рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно.

Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т. е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S³ выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S³ стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т. е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь.

Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R³, что облегчает их визуализацию. Для трехмерной сферы S³ (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение.

По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S³ — это при помощи одноточечной компактифика-ции. А именно, трехмерная сфера S³ представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R³.

Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность — одномерный аналог сферы.

Подобным же образом, если я возьму бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S². Эту процедуру можно наблюдать при помощи стереографической проекции, которая каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P’:

Таким образом, сфера без одной точки — это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу.

В принципе, точно такая же конструкция применима и к трехмерной сфере и трехмерному пространству, только для ее осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. Поэтому я ограничусь словесным описанием одноточечной компактификации пространства R³.

Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т.е. каждая пространственная прямая замыкается в окружность). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S³.

Легко понять, что сфера S³ односвязна. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R³, которая легко стягивается в точку посредством гомотетий, т. е. непрерывного сжатия по всем трем направлениям.

Для понимания, как устроено многообразие S³, весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R³ выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S³ разбивается на два полнотория, имеющих общую границу — тор.

Вот как это можно понять. Вложим тор в R³ как обычно, в виде круглого бублика, и проведем вертикальную прямую — ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет наше полноторие по двум кругам, показанным на рисунке зеленым цветом, а дополнительная часть плоскости разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, выделенная более жирно, потому что в сфере S³ прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомео-морфное полноторию, только выглядящее необычно.

В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей — окружностей, составляющих обычное полноторие.

Чтобы было с чем сравнивать 3-сферу, я приведу еще один пример компактного 3-многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб:

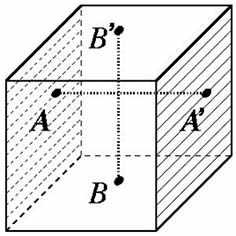
В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A’ — это одна и та же точка, а B и B’ — тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб-это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A’ в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора.
Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх — и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная.
На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA’ на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A’ обязаны двигаться по своим граням, оставаясь строго друг напротив друга (иначе кривая разомкнется).
Итак, мы видим, что бывают односвязные и неодносвязные компактные 3-многообразия. Перельман доказал, что односвязное многообразие ровно одно.
Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т.е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, — в трехмерном случае поток Риччи способен портить многообразие, т. е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, а в конце концов оно превращается в круглую сферу. Но нужно объяснить наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому я ограничусь описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость.
Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она более плавная, кривизна будет меньше.
Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение на зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например, окружность радиуса 1 имеет постоянную положительную кривизну, равную 1 (если считать ее в радианах).
Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот пример:
Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т. е. превращается в конце концов в окружность. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, просто способ доказательства иллюстрирует, что происходит в размерности 3).
Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и гораздо более общую гипотезу геометризации Тёрстона, которая в известном смысле описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи.
Сергей Дужин,
докт.физ.-мат. наук,
старший научный сотрудник
Санкт-Петербургского отделения
Математического института РАН
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Связанные статьи
trv-science.ru
История науки: гипотеза Перельмана. Математика и Computer Science
Чтобы понять гипотезу Пуанкаре, математики предлагают провести мысленный эксперимент, например такой: «Возьмем ракету и привяжем к ней очень длинную веревку и запустим ракету в космос. Ракета с привязанной к хвосту веревкой облетает всю Вселенную и благополучно возвращается на Землю. И теперь у вас в руках оба конца веревки, которую протащили через всю Вселенную. Получилась гигантская петля. Теперь можно вытянуть всю веревку, стягивая петлю. Когда мы вытянем ее всю, что мы сможем сказать о форме Вселенной? Если вы протащите веревку через всю Вселенную и в любом случае сможете стянуть ее до конца, разве вы не признаете, что Вселенная в принципе имеет форму шара?» Таким образом мы бы доказали, что Вселенная представляет собой односвязное многообразие, то есть ее можно стянуть в точку, а, следовательно, и ее появление даже из бесконечно малого «зародыша» не противоречит топологии. Однако если это не удастся, то получается, что Вселенная обладает более сложной топологией, как минимум не проще, чем у тора. Так доказательство гипотезы приобретает мировоззренческое значение.
Человек не может взглянуть на Вселенную со стороны, однако Пуанкаре предположил, что можно математически доказать принадлежность формы Вселенной к тому или иному классу, что и предполагает гипотеза. Первые два доказательства — самого Пуанкаре и человека, обратившего внимание математиков на гипотезу, Джона Уайтхеда, — быстро были опровергнуты самими авторами. Однако интерес к гипотезе нарастал: доказать ее пытались лучшие умы, но безуспешно. Иногда, как в случае математика греческого происхождения Христоса Папакириакопулоса, стремление найти доказательство приобретало характер одержимости, но не приводило к значительным подвижкам. Другому математику, американцу Стивену Смейлу, удалось доказать гипотезу, но только для пространства с большим, чем четыре, числом измерений. Еще один американец, Майкл Фридман, доказал гипотезу для четырехмерного пространства, за что получил медаль Филдса. Однако использовать эти достижения для трехмерного пространства было невозможно.
Найти доказательство гипотезы удалось лишь через 98 лет после ее создания российскому математику Григорию Перельману. Он опубликовал в электронном архиве научных статей и препринтов три статьи, по сути, содержащие это доказательство. По сути — потому что обоснованные в них положения не являются доказательством гипотезы Пуанкаре, но снимают основные проблемы, стоявшие перед математиками. Перельман сделал основную часть работы, оставив приведение доказательства к законченному виду своим коллегам. На это ушло несколько лет: задача осложнялась тем, что в работе использовались не привычные топологам методы, а принципы и понятия дифференциальной геометрии и физики.
Так как заявления о том, что доказательство найдено, звучали уже не раз, неудивительно, что поначалу и к статьям Перельмана отнеслись скептически. Его приглашали в Принстон и другие ведущие университеты с циклом лекций, раскрывающих смысл доказательства. И лишь в 2006 году было вынесено решение — доказательство Перельмана верно, а гипотезу Пуанкаре следуют считать доказанной. За это Перельману присудили премию Филдса, однако принять ее он отказался.
indicator.ru
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Навигация по записям
Previous post: Нижняя опора двигателя форд фокус 2 – Замена нижней (задней) опоры двигателя — бортжурнал Ford Focus Hatchback 2008 года на DRIVE2
Next post: Фокус 3 краш тест – ЖЕСТЬ! Краш-тест Ford Focus на скорости 192 км/ч (120 миль/ч)

Запасные части и аксессуары для автомобилей ФОРД