Зависимость периметра от площади – Как найти площадь, зная периметр 🚩 Найти периметр прямоугольника зная его площадь 🚩 Математика
Периметр и площадь прямоугольника
Можно ли найти площадь из периметра?
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя.
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. ( 1 + 9 ) * 2 = 20 точно также как и ( 2 + 8 ) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S1 = 1 * 9 = 9 см2
S2 = 2 * 8 = 16 см2
S3= 3 * 7 = 21 см
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
-
Задача 1. Найти стороны прямоугольника из площади
- Задача 2. Найти стороны прямоугольника из периметра
- Задача 3. Найти площадь прямоугольника из пропорции его сторон
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x2+2y2=260
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=16
x=16-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
2(16-y)2+2y2=260
2(256-32y+y2)+2y2=260
512-64y+4y2-260=0
4y2-64y+252=0
Решаем полученное квадратное уравнение.
D=4096-16×252=64
x
x2=7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ: Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x2+y2=89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
169-26y+y2+y2-89=0
2y2-26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x1=5
x2=8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см
Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?Решение.
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S2 = S / 1.25
S2 = 1,25ab / 1.25
поскольку новый размер а изменять нельзя, то
S2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на ( 1 — 0,8 ) * 100% = 20%
Ответ: ширину нужно уменьшить на 20%.
profmeter.com.ua
Как соотносятся периметр и площадь? — Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
Авторы работы
Группа «Землемеры», участники проекта «Фигуры в клеточку», ученики 5 класса
Проблемный вопрос (вопрос для исследования)
Как соотносятся площади и периметры фигур?
Цели исследования
Выявить зависимость между периметрами фигур и их площадью.
Гипотеза
Чем больше периметр, тем больше площадь фигуры.
Что нужно выяснить?
Какие свойства периметра и площади фигур?
Как связаны периметры и площади прямоугольников?
Какая фигура имеет наибольшую площадь при заданном периметре?
Какие единицы измерения площади используются для измерения земли?
Результаты проведённого исследования
Вывод
1. Если периметр одного прямоугольника больше, то и его площадь больше, чем у других.
2. Ели периметры прямоугольников равны, то площади могут быть различны.
3. Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.
4. У равновеликих фигур чем больше вершин, тем больше периметр.
5. Для решения изопериметрических задач надо уметь вычислять площади разных многоугольников и круга.
Ресурсы
Единицы измерения
Изопериметрическая задача
Изопериметрическая задача и некоторые другие задачи на максимум и минимум
Занимательная геометрия, Перельман Яков
Другие статьи про периметр, площадь и фигуры
Площадь прямоугольника.Из истории геометрии
Результат исследования ученика в проекте Геометрические фигуры в пространстве
Другие документы
Исследование зависимости периметра и площади прямоугольников.
wiki.iteach.ru
Исследование площади прямоугольника данного периметра
Просмотр содержимого документа
«Исследование площади прямоугольника данного периметра»

Исследование площади прямоугольника данного периметра
Автор: Косова Татьяна Анатольевна
Kosova Tatyana
Учитель математики МБОУ г.Шахты Ростовской области «Гимназия имени А.С.Пушкина»

Аннотация
Данная методическая разработка представляет собой описание опыта её автора, связанного с применением метода исследовательской работы с учащимися на уроках математики и во время внеклассных занятий по предмету.
Автором является Косова Татьяна Анатольевна учитель математики МБОУ г.Шахты Ростовской области «Гимназия имени А.С. Пушкина».

Цель исследования
Выявить зависимость между изменением длины одной из сторон прямоугольника и площадью при заданном периметре прямоугольника.
Гипотеза
С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника.
Как связаны периметры и площади прямоугольников?
Какой прямоугольник имеет наибольшую площадь при заданном периметре?
Что нужно выяснить:

Мы знаем:
Периметр – сумма длин всех сторон многоугольника.
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости

Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?
Сначала мы рассмотрим прямоугольники.
Заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других.
Но если периметры равны, то площади могут быть различны.
От чего зависят площади прямоугольников, если их периметры равны?

Какой из всех прямоугольников заданного периметра имеет наибольшую площадь?
Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида.
Задача
Периметр прямоугольника равен 24см, а его основание х (см). Задайте формулой зависимость площади S ( ) прямоугольника от х.
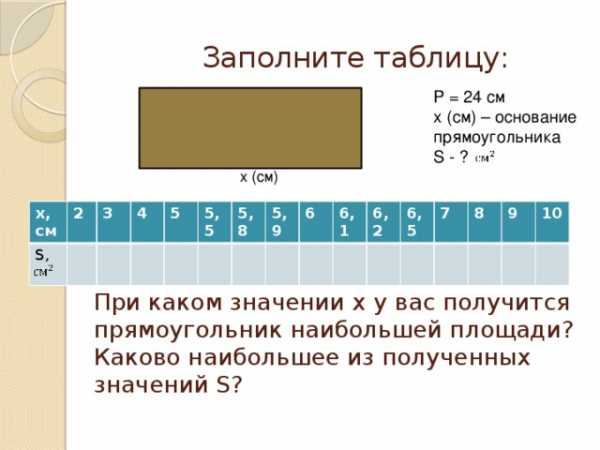
Заполните таблицу:
P = 24 см
х (см) – основание прямоугольника
S — ?
х, см
2
S,
3
4
5
5,5
5,8
5,9
6
6,1
6,2
6,5
7
8
9
10
При каком значении х у вас получится прямоугольник наибольшей площади? Каково наибольшее из полученных значений S?

- Выберите сами два каких-либо значения х и вычислите соответствующие значения S. Удалось ли вам получить значение S, большее, чем найденное ранее?
- Какую гипотезу (гипотеза – научное предположение) можно высказать на основании проведённого исследования о форме прямоугольника наибольшей площади, имеющего данный периметр?

Вывод
1. Если периметры прямоугольников равны, то площади могут быть различны.
2. Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.

Используемые источники: 1. К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. «Алгебра 7 класс».
multiurok.ru
Формула треугольника: площадь и периметр
Найти площадь треугольника вы можете, воспользовавшись онлайн-программами, а на этой странице мы ознакомимся с формулами площади и периметра треугольника.
Треугольник – геометрическая фигура, которая состоит из 3 точек, не лежащих на одной прямой, и попарно соединенных 3 отрезками.
Площадь треугольника – это положительная величина, которая характеризует геометрическую фигуру (треугольник) и числовое значение которой выражается квадратными единицами.
Содержание статьи:
Формула площади треугольника
$S = \frac12{ah}$
a — сторона треугольника;
ha — высота, проведенная к стороне а.
$S = \frac12{abSinC}$
a, b — стороны треугольника;
C — угол между сторонами a и b.
Формула Герона
$S = \sqrt{p(p-a)(p-b)(p-c)}$a, b, c — стороны треугольника;
$p= \frac{a+b+c}{2}$ — полупериметр.
$S=pr$
$p= \frac{a+b+c}{2}$ — полупериметр треугольника;
r — радиус вписанной в треугольник окружности.
$S=\frac{abc}{4R}$
a, b, c — стороны треугольника;
R — радиус описанной окружности.
Формула площади равнобедренного треугольника
Равнобедренным называется треугольник, у которого две стороны равны.
$S=\frac{b}{4}\sqrt{4a^2-b^2}$
a, b — стороны равнобедренного треугольника.
Формула площади равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Медиана, высота, биссектриса равностороннего треугольника, проведенные с одной вершины — совпадают.
$S=\frac{a^2\sqrt3}{4}$
a — сторона равностороннего треугольника.
$S=\frac{m^2\sqrt3}{3}$
m — медиана (высота, биссектриса).
$S=\frac{3R^2\sqrt3}{4}$
R — радиус описанной окружности.
$S=3r\sqrt3$
r — радиус вписанной окружности.
Формула площади прямоугольного треугольника
Прямоугольным называется треугольник, если он имеет прямой угол. АС и ВС — катеты, АВ — гипотенуза.
$S=\frac12{ab}$
a, b — катеты.
$S=\frac12{ch_{c}}$
c — гипотенуза;
hc — высота, проведенная к гипотенузе.
Формула периметра треугольника
Периметр треугольника равен сумме длин всех его сторон (a, b, c).
$P=a+b+c$
P — периметр;
a, b, c — стороны треугольника.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Как рассчитать площадь и периметр помещения и в каких случаях следует ее знать?
Главная / Монтаж, ремонт, уход / Рассчитываем площадь и периметр помещения
Любое важное начинание надо просчитывать заранее, ремонт не исключение. Поскольку затраты предстоят большие, надо их оптимизировать и уменьшить по максимуму, особенно, если хочется сделать что-то дорогостоящее, например натяжные потолки с несколькими уровнями. Если покупать материалы «на глазок», легко можно ошибиться – купить или слишком много или придется идти в магазин и докупать недостающие стройматериалы. Для того, чтобы не купить лишнего дорогого стройматериала и сэкономить семейный бюджет, надо знать, как рассчитать площадь помещения. Вот с этого то и начнем.

В каких случаях нужны расчеты?
Расчет квадратных метров обязателен, если в проекте установить подвесные потолки. Для наглядности посмотрим, что нужно для гипсокартонных конструкций. Площадь комнаты рассчитывается, чтобы закупить гипсокартон в нужном количестве, а периметр надо знать для покупки пристенного профиля для установки обрешетки. Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.
Для заказа натяжного потолка делать расчет квадратуры комнаты требуется, что запланировать будущие траты и проконтролировать фирму-установщика в правильности их расчетов. Фирма, изготавливающая натяжные потолки обычно указывает цену за квадратный метр и плюсует работу по установке. Зная площадь и стоимость квадрата, можно легко определить конечную цену.
Вычислить площадь требуется даже для банальной покраски пола или потолка, чтобы знать, сколько закупать краски. Важно купить нужное количество краски, иначе если не хватит, а краску в магазине колорировали, то можно не угадать с цветом. Примерный расход краски на метр квадратный поверхности указывается на банке.
Пример расчета потребности в краске:
Квадратура пола составляет 30 м2
расход краски согласно данным на упаковке – 0,20 кг/м2
30 х 0,2 = 6 кг
Полагается брать краску свыше расчетного количества на 10%.
Поэтому получаем 6 + 10% = 6,6 кг. Это подойдет ведро 7 кг или приближенная расфасовка в зависимости от вида краски.
Как посчитать площадь комнаты
Если вы владелец небольшой прямоугольной комнаты, то большого труда вычислить квадратуру комнаты это не составит. Достаточно вспомнить школьный курс геометрии. А что делать, если на месте потолка сложный многоугольник или имеются всевозможные ниши или выступы?
Прямоугольная комната
Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса. К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м. Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.
Комната сложной формы
Очень часто в домах старой постройки встречаются комнаты с нишами, выступами, встроенными кладовками. Нам предстоит решить задачку посложнее, но оказывается все просто. Потребуется лист в клетку или простой, на котором мы нарисуем эскиз комнаты с приблизительным сохранением пропорций. Далее измеряем метраж прямых стен и записываем на эскизе рядом с соответствующими линиями, обозначающими стены.
А вот теперь порисуем. Эскиз надо разбить на прямоугольники при помощи угольника и линейки, соблюдая прямые углы. Причем, одной из сторон прямоугольника должна быть измеренная полная стена. Теперь надо вычислить квадратные метры каждого из нарисованных прямоугольников и суммировать их. Периметр вычислить в любом случае проще – просто складываем длины всех стен и закоулочков.
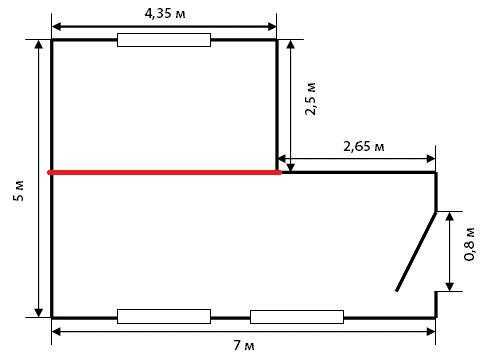
Расчет площади многогранной комнаты
Что делать, если в комнате есть «срезанные» или не прямые углы? Нам предстоит задача в три действия, но сначала опять же замеряем все стены, не забывая про скосы, и рисуем эскиз. Вот, как этот к примеру.
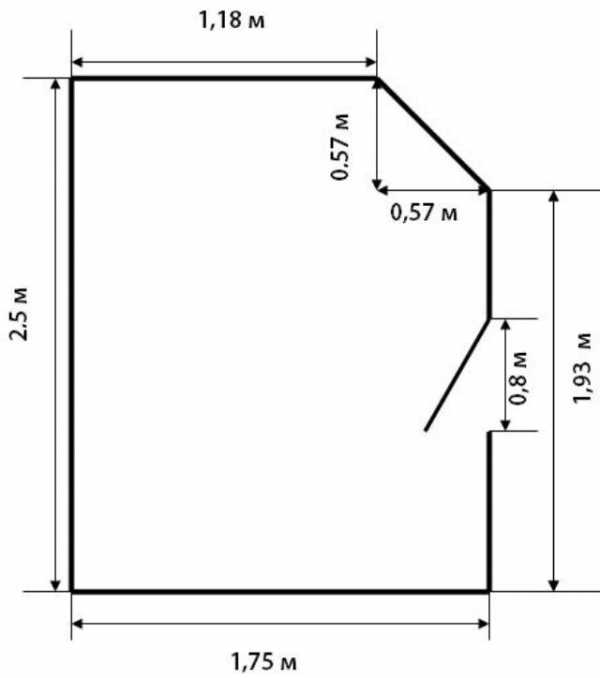
Теперь начинается чистая геометрия. Первое действие – принимаем наш скос за гипотенузу прямоугольного треугольника, соединяем катеты. Остается применить формулу для вычисления прямоугольного треугольника, которая выглядит следующим образом: S = катет х катет /2. Катет у нас вычисляется так: известная длина стены равная 1,75 м (см. чертеж) минус противоположная стена 1,18 м. Получаем 0.57 м. Аналогично вычисляем другой катет, используя длины других противоположных стен.
Исходя из этого найдем площадь треугольника 0,57 х 0,57 / 2 = 0.57 м2
Второе действие – разделение комнаты на два прямоугольника без учета уже посчитанного треугольника. См. рисунок.
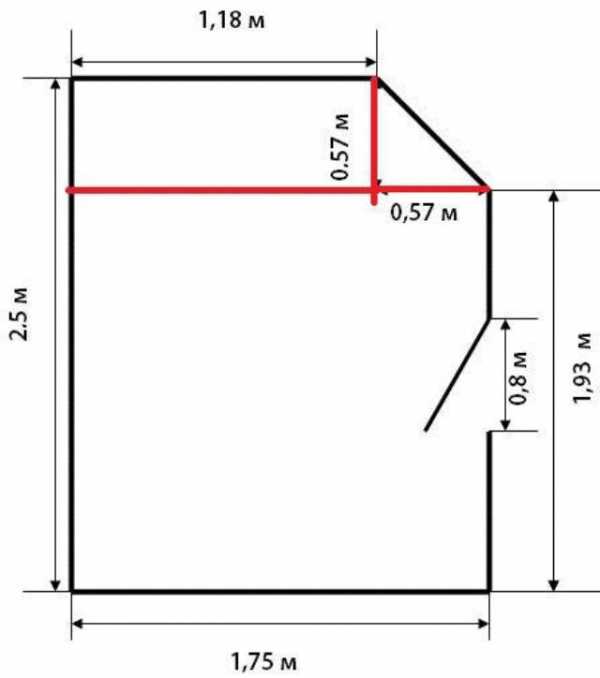
Далее повторяем расчеты в предыдущем примере для комнаты с нишей. Затем останется сложить площади всех полученных простых фигур, и получим квадратуру помещения.
В заключение
Не стоит скрупулезно обмерять и высчитывать все значения. В любом случае будет погрешность около 5%, но сколь либо серьезно это значение не влияет на расчеты. Можно не брать во внимание небольшие скругления углов. Если надо рассчитать площадь стен для закупки отделочных материалов, то действуем по первому примеру с правильным прямоугольником, вычитая площадь окон и дверей. В наших домах стандартная высота потолков может разниться в каждом из углов, поэтому берем большее значение с учетом обрезки. Пусть лучше будет небольшой запас, чем потом думать, как выйти из ситуации. Удачи вам в ремонте!
wikipotolok.com
Зависимость площади от периметра прямоугольника
Вычислите площадь фигуры, ограниченной линиями y=x^3-1, x=2, y=0.
Зависимость площади от периметра прямоугольника
Глава 12. Соотношение периметра и площади
Для окружностей, квадратов, равносторонних треугольников и других многоугольников отношение периметра к квадратному корню их охватываемой площади
Не зависит от размера многоугольника. Отношение одинаково для каждого семейства замкнутых кривых одинаковой формы. Для окружностей, квадратов и равносторонних треугольников это отношение равно соответственно и 6/31/4.
Для семейства подобных островов различных размеров отношение длины нефрактальной береговой линии любого острова к квадратному корню из его площади не зависит от размера острова. Однако, если береговая линия фрактальна, то ее длина зависит от длины эталона 5, с помощью которого меряется длина и при Напротив, площадь острова измеряемая с помощью его покрытия квадратами площадью 52, остается конечной при 5 0. Как показал Мандельброт, для фрактальных кривых расходящееся отношение следует заменить в каждом случае следующей модификацией:
Здесь фрактальная размерность береговых линий островов, имеющих подобные очертания. Отношение не зависит от размера острова, но оно зависит от выбора эталона длины.
Соотношение периметра и площади, выраженное равенством (12.1), вытекает из определения фрактальной размерности содержащегося в выражениях (2.3) и (2.4). Это можно усмотреть из сравнения двух подобных островов разной площади, показанных на рис. 12.1. Площадь и длина береговой линии каждого из островов измеряются с помощью эталона, длина которого зависит от площади данного острова. Площадь острова равна когда она измеряется эталоном фиксированной длины 5, а параметр — некоторое произвольно малое число, скажем, 0,0001. Длина береговой линии острова равна периметру многоугольника, состоящего из отрезков длины, т. е. в этом приближении
Рис. 12.1. Два подобных острова, обмеряемые с помощью эталона, длина которого зависит от площади острова.
Теперь можно сделать важное замечание: для подобных островов не зависит от размера острова. Однако из соотношения (2.3) следует, что длина береговой линии острова равна Таким образом, мы приходим к равенству
Выразим 5 через
И получим, что отношение
Не зависит от размера острова. Однако это отношение зависит от длины 8 используемого эталона и принятого значения произвольного множителя Поэтому, несмотря на то что связано с формой островов, эта величина включает также произвольные множители, и мы по-прежнему не имеем общей характеристики формы острова. Можно заключить, что острова, очертания которых подобны, удовлетворяют соотношению периметра и площади
Полученному Мандельбротом. Это соотношение удовлетворяется для любого эталона длины 8, достаточно малого, чтобы удовлетворительно обмерять самый малый из островов. Коэффициент пропорциональности зависит от произвольного параметра Соотношение (12.2)
Лежит в основе практического определения фрактальной размерности в нескольких интересных случаях, обсуждаемых в последующих разделах.
Чтобы привести пример соотношения периметра и площади, рассмотрим остров, ограниченный квадратичной кривой Кох (см. рис. 2.9). Первичным элементом кривой является квадрат со стороной а. Генератор кривой при замене каждой ее стороны добавляет малый «полуостров» и вырезает участок «побережья» такого же размера. Поэтому при повторных преобразованиях кривой не меняется охватываемая ею площадь Периметр кривой порядка, равен длине береговой линии, если она измеряется с помощью эталона длины Поэтому порядок кривой можно выразить через ее площадь, и мы получаем Здесь есть фрактальная размерность береговой линии острова, ограниченного квадратичной кривой Кох. Итак, такие острова удовлетворяют соотношению периметра и площади вида (12.2) с коэффициентом пропорциональности
Другой пример связан с триадной кривой Кох. Здесь под островом будем понимать участок плоскости, заключенный между начальным элементом, т. е. отрезком длины а, и предельной кривой Кох (см. рис. 2.8). Охватываемая площадь равна а полная длина береговой линии порядка равна если используется эталон длины Это приводит к равенству
Как видим, если пренебречь первым членом в правой части, то получится соотношение периметра и площади (12.2). Отброшенный член представляет собой нефрактальный прямой участок границы островов. Этот пример показывает, что соотношение периметра и площади (12.2) может быть справедливо только в пределе малой длины эталона 5, когда длина фрактальной части береговой линии преобладает над вкладом любой регулярной части береговой линии. Нетрудно построить более сложные примеры, в которых разные участки берега имеют разные фрактальные размерности. В этом случае анализ показывает, что отношение периметра и площади определяется наибольшим значением фрактальной размерности.
Глава 4. Образование вязких пальцев в пористых средах
Глава 5. Канторовские множества
Глава 8. Фрактальные временные ряды
Глава 12. Соотношение периметра и площади
Глава 13. Фрактальные поверхности
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
Зависимость площади от периметра прямоугольника
Исследование учащихся: Как соотносятся периметр и площадь?
Содержание
Авторы работы
Группа «Землемеры», участники проекта «Фигуры в клеточку», ученики 5 класса
Проблемный вопрос (вопрос для исследования)
Как соотносятся площади и периметры фигур?
Цели исследования
Выявить зависимость между периметрами фигур и их площадью.
Что нужно выяснить?
Какие свойства периметра и площади фигур?
Как связаны периметры и площади прямоугольников?
Какая фигура имеет наибольшую площадь при заданном периметре?
Какие единицы измерения площади используются для измерения земли?
Результаты проведённого исследования
1. Если периметр одного прямоугольника больше, то и его площадь больше, чем у других.
2. Ели периметры прямоугольников равны, то площади могут быть различны.
3. Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.
4. У равновеликих фигур чем больше вершин, тем больше периметр.
5. Для решения изопериметрических задач надо уметь вычислять площади разных многоугольников и круга.
Зависимость площади от периметра прямоугольника
Исследование учащихся: Как соотносятся периметр и площадь?
Содержание
Авторы работы
Группа «Землемеры», участники проекта «Фигуры в клеточку», ученики 5 класса
Проблемный вопрос (вопрос для исследования)
Как соотносятся площади и периметры фигур?
Цели исследования
Выявить зависимость между периметрами фигур и их площадью.
Что нужно выяснить?
Какие свойства периметра и площади фигур?
Как связаны периметры и площади прямоугольников?
Какая фигура имеет наибольшую площадь при заданном периметре?
Какие единицы измерения площади используются для измерения земли?
Результаты проведённого исследования
1. Если периметр одного прямоугольника больше, то и его площадь больше, чем у других.
2. Ели периметры прямоугольников равны, то площади могут быть различны.
3. Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.
4. У равновеликих фигур чем больше вершин, тем больше периметр.
5. Для решения изопериметрических задач надо уметь вычислять площади разных многоугольников и круга.

poiskvstavropole.ru
ПНШ 4 класс. Математика. Учебник № 1, с. 40
Зависимость между величинами
Ответы к с. 40
112. Приведи пример двух величин, которые находятся в некоторой зависимости одна от другой, а также двух величин, которые не зависят друг от друга.
Зависят.
Количество тарелок на столе в столовой от количества обедающих учеников. Количество учебников в портфеле ученика от количества уроков в школе.
Не зависят.
Время начала уроков в школе от количества учеников в классе. Количество дней в каникулах от погоды.
113. Заполни в тетради данную таблицу, если известно, что длина α на 3 см больше, чем длина b.
| α (см) | 12 | 65 | 50 | 187 | 4568 |
| b (см) | 9 | 62 | 47 | 184 | 4565 |
Будет ли в данном случае величина b однозначно зависеть от величины α?
Величина b однозначно зависит от величины α, так как при каждом значении α, можно найти единственное значение b.
114. Если известен периметр квадрата, то можно ли однозначно установить его площадь? Сделай это для квадрата, периметр которого равен 20 см.
Объясни, почему площадь квадрата однозначно зависит от его периметра.
Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.
1) 20 : 4 = 5 (см) — одна сторона
2) 5 • 5 = 25 (кв. см) — площадь
Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.
115. Начерти два прямоугольника, у одного из которых стороны имеют длину 6 см и 4 см, а у другого соответственно 8 см и 2 см. Вычисли периметр и площадь каждого из этих прямоугольников. Сравни получившиеся периметры между собой и получившиеся площади между собой.
Если известен периметр прямоугольника, то можно ли однозначно установить его площадь?
Объясни, почему площадь прямоугольника не будет однозначно зависеть от го периметра. А что можно сказать о зависимости площади квадрата от его периметра? Проиллюстрируй это на примере.
Первый прямоугольник: Р = (6 + 4) • 2 = 20 (см), S = 6 • 4 = 24 (кв. см).
Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (кв. см).
Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника: 24 кв. см > 16 кв. см.
По известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
Площадь квадрата однозначно зависит от его периметра. Это видно из предыдущего задания №114: каждому значению периметра квадрата соответствует единственное значение площади.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
Математика. 4 класс. Чекин А.Л.
ПНШ 4 класс. Математика. Учебник № 1, с. 40
Понравилось? Оцени!e-razumniki.ru