Фигура с бесконечным периметром – ,

Парадокс маляра — Энциклопедия научных парадоксов

Материал из Энциклопедия научных парадоксов

Это — материал о парадоксах.

Бесконечная пластинка и тело, образованное её вращением

Парадокс маляра́ — математический парадокс, утверждающий, что фигуру с бесконечной площадью поверхности можно окрасить конечным количеством краски.

Рассмотрим бесконечную ступенчатую пластинку, состоящую из прямоугольников: первый из них — квадрат со стороной 1 см, второй имеет размеры 0,5 x 2 см, а каждый следующий вдвое у́же и вдвое длиннее предыдущего. Площадь каждого прямоугольника равна 1 см², а общая площадь пластинки бесконечна.

Чтобы всю её покрасить, потребуется бесконечное (по объёму или массе) количество краски. Рассмотрим тело, получаемое при вращении пластинки вокруг её прямого бесконечного края. Сосуд состоит из цилиндров. Высота

k-го цилиндра равна 2k−1{\displaystyle 2^{k-1}} см, радиус — 21−k{\displaystyle 2^{1-k}} см, а значит, его объём равен 21−kπ{\displaystyle 2^{1-k}\pi } см³. Таким образом, объёмы цилиндров образуют убывающую геометрическую прогрессию, их сумма конечна и равна 2π{\displaystyle 2\pi } см³.

Заполним этот сосуд краской. Погрузим в него данную бесконечную пластинку и вытащим; она будет окрашена конечным количеством краски с двух сторон.

Разрешение парадокса[править]

Утверждение «для того, чтобы покрасить фигуру бесконечной площади, необходимо бесконечное количество краски» исходит из того, что фигура покрывается слоем краски одинаковой толщины.

Предлагаемый же способ окраски предполагает, что каждый следующий сегмент будет покрыт всё более тонким слоем, так что бесконечная сумма объёмов краски, ушедших на каждый сегмент площадью в 1 см², будет сходиться к конечному значению.

paradox.pifia.ru

Снежинка Коха

 

Эта фигура — один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше (Карл Вейерштрасс построил свой пример еще в 1872 году), но кривая Коха замечательна простотой своей конструкции. Не случайно его статья называется «О непрерывной кривой без касательных, которая возникает из элементарной геометрии».

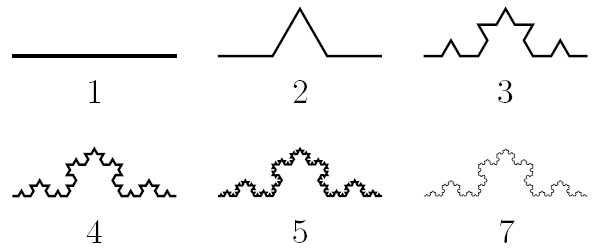
Рисунок и анимация отлично показывают, как по шагам строится кривая Коха. Первая итерация — просто начальный отрезок. Потом он делится на три равные части, центральная достраивается до правильного треугольника и затем выкидывается. Получается вторая итерация — ломаная линия, состоящая из четырех отрезков. К каждому из них применяется такая же операция, и получается четвертый шаг построения. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха.

Основные свойства кривой Коха

1. Она непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».

2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)^n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.

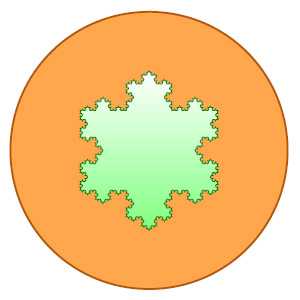
3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе. Для интересующихся вычисление приведено ниже мелким шрифтом.

Пусть сторона исходного правильного треугольника равна a. Тогда его площадь . Сначала сторона равна 1, а площадь: . Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n-м шаге будет достроено T_n = 3 · 4^n–1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3)

ⁿ. Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна . При больших значениях n это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равен T_n · S_n = 3/4 · (4/9)ⁿ · S₀. Поэтому после n-го шага площадь фигуры будет равна сумме S₀ + T₁ · S₁ + T₂ · S₂ + … +T_n · S_n = . Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула: . Площадь снежинки равна .

4. Фрактальная размерность равна log4/log3 = log₃4 ≈ 1,261859… . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности. Из формулы степенной зависимости

N(δ) ~ (1/δ)^D, где N — число пересекающихся квадратиков, δ — их размер, а D — размерность, получаем, что D = log_1/δN. Это равенство верно с точностью до прибавления константы (одной и той же для всех δ). На рисунках изображена пятая итерация построения кривой Коха, зеленым закрашены квадратики сетки, которые с ней пересекаются. Длина исходного отрезка равна 1, поэтому на верхнем рисунке длина стороны квадратиков равна 1/9. Закрашено 12 квадратиков, log₉12 ≈ 1,130929… . Пока не очень похоже на 1,261859… . Смотрим дальше. На среднем рисунке квадратики в два раза меньше, их размеры 1/18, закрашено 30. log₁₈30 ≈ 1,176733… . Уже лучше. Внизу квадратики еще вдвое меньше, закрашено уже 72 штуки. log₇₂30 ≈ 1,193426… . Еще ближе. Дальше нужно увеличивать номер итерации и одновременно уменьшать квадратики, тогда «эмпирическое» значение размерности кривой Коха будет неуклонно приближаться к log

34, а в пределе и вовсе совпадет.

Варианты

Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.

Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°.

Квадратный вариант. Тут достраиваются квадраты.

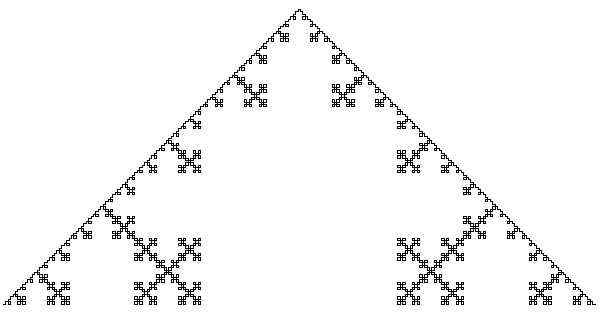
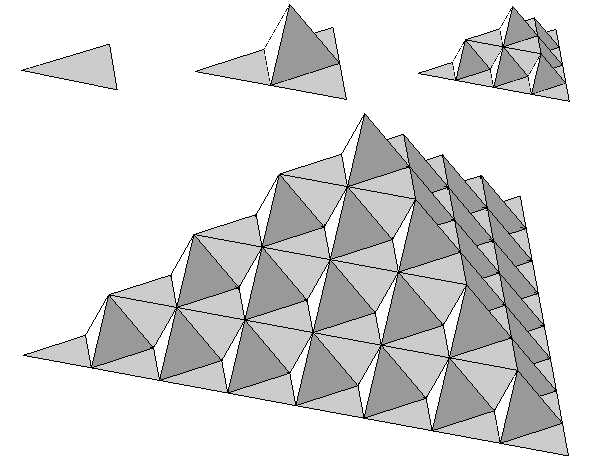
Трехмерные аналоги. Пирамида Коха.

Далее: Т-квадрат

elementy.ru

Фигура, имеющая нулевую площадь и бесконечный периметр. : Геометрия

Недавно придумал такую вот задачу.
Укажите плоскую фигуру (замкнутую кривую с возможными самопересечениями) в квадрате , имеющую строго нулевую площадь и строго бесконечный периметр.
Мои скромные мысли:
Очевидно, что существует полно фигур со сколь угодно большим периметром и сколь угодно малой площадью, однако они меня не интересуют.
Пример такой фигуры :
Стоящие рядом равнобедренные треугольники с единичной высотой и основанием количеством штук.

Тогда площадь фигуры , периметр
Несколько вопросов, которые могут возникнуть:
1) Что значит замкнутая кривая. Кривая Жордана: образ непрерывного инъективного отображения окружности в пространство.
2) Что значит указать фигуру (кривую). Указать её построение и доказать (если это не очевидно), что она является кривой Жордана.
Например, я не знаю, существует ли предел указанной выше последовательности кривых и является ли он кривой по Жордану. Мне кажется, что нет. Но если бы существовал, то он бы как раз и имел нулевую площадь и бесконечный периметр.
3) Что такое площадь и периметр. Меру берите какую вам угодно, если выбора зависит ответ задачи. Лично я пока знаком только с мерой Жордана. В частности, имеется подозрение, что выбрав меру Жордана, мы сможем доказать несуществование замкнутой кривой с нулевой площадью и бесконечным периметром. Вполне возможно, что это следует прямо из определения кривой.
Жду ответов. Не исключаю того, что вопрос может являться совершенно тривиальным:)

dxdy.ru

Мятый рубль — Математические этюды

По­сле вой­ны, в 1947 го­ду, в СССР бы­ли вве­де­ны день­ги но­во­го об­раз­ца. И хо­тя в 1956 го­ду Ка­ре­ло-Фин­ская Со­вет­ская Со­ци­а­ли­сти­че­ская рес­пуб­ли­ка бы­ла воз­вра­ще­на в со­став РСФСР, и, со­от­вет­ствен­но, ко­ли­че­ство лен­то­чек на гер­бе умень­ши­лось, год на банк­но­тах ме­нять не ста­ли.

В том же 1956 го­ду Вла­ди­мир Иго­ре­вич Ар­нольд по­ста­вил за­да­чу о мя­том руб­ле. Мож­но ли сло­жить пря­мо­уголь­ный лист бу­ма­ги (рубль) в плос­кий мно­го­уголь­ник так, чтобы пе­ри­метр ко­неч­но­го мно­го­уголь­ни­ка был боль­ше пе­ри­мет­ра ис­ход­но­го пря­мо­уголь­ни­ка?

В 1961 го­ду на­шу стра­ну по­стиг­ла но­вая ре­фор­ма де­нег. Ди­зайн рублё­вой банк­но­ты из­ме­нил­ся, её физи­че­ский раз­мер стал го­раз­до мень­ше. К это­му вре­ме­ни за­да­ча всё ещё не бы­ла ре­ше­на.

Кро­ме то­го, что по­ло­жи­тель­ный от­вет «мож­но» про­ти­во­ре­чит ин­ту­и­ции, есть и ма­те­ма­ти­че­ские до­во­ды в поль­зу от­ри­ца­тель­но­го от­ве­та. Ес­ли сло­жить пря­мо­уголь­ник вдоль пря­мой, то пе­ри­метр толь­ко умень­шит­ся: к уже су­ще­ство­вав­шей гра­ни­це при­бав­ля­ет­ся от­ре­зок той пря­мой, вдоль ко­то­рой скла­ды­ва­ет­ся, а уко­ра­чи­ва­ет­ся гра­ни­ца на ло­ма­ную с те­ми же кон­ца­ми, что и от­ре­зок. Ес­ли сде­лать ана­ло­гич­ную опе­ра­цию — сло­жить от­но­си­тель­но пря­мой весь уже по­лу­чив­ший­ся мно­уголь­ник, — то си­ту­а­ция бу­дет та­кая же: пе­ри­метр уве­ли­чи­ва­ет­ся на дли­ну от­рез­ка, а умень­ша­ет­ся на дли­ну ло­ма­ной. Та­кое скла­ды­ва­ние — от­но­си­тель­но пря­мой — на­зы­ва­ет­ся «про­стым» и все­гда толь­ко умень­ша­ет пе­ри­метр. Но это толь­ко до­во­ды, но ещё не до­ка­за­тель­ство.

Так мож­но или нель­зя уве­ли­чить пе­ри­метр из­на­чаль­но­го пря­мо­уголь­ни­ка? В ре­фор­мах 1991 и 1993 го­дов рубль об­раз­ца 61 го­да был вы­ве­ден из об­ра­ще­ния, а за­да­ча В. И. Ар­ноль­да так и оста­ва­лась нере­шён­ной.

С тех пор один рос­сий­ский рубль — это, к со­жа­ле­нию, на­столь­ко ма­ло, что бу­маж­ных банк­нот та­ко­го до­сто­ин­ства уже не вы­пус­ка­ют, лишь ме­тал­ли­че­ские мо­не­ты.

В на­ча­ле XXI ве­ка за­да­ча всё же бы­ла ре­ше­на. Пер­вое ма­те­ма­ти­че­ски стро­гое ре­ше­ние дал уче­ник Ни­ко­лая Пет­ро­ви­ча Дол­би­ли­на — Алек­сей Та­ра­сов. Он пред­ло­жил ал­го­ритм, как скла­ды­вать квад­рат так, чтобы в ито­ге по­лу­чил­ся плос­кий мно­го­уголь­ник с боль­шим пе­ри­мет­ром.

Для тех, кто хо­чет про­сто лю­бо­вать­ся филь­мом, сле­ду­ю­щий аб­зац мож­но про­пу­стить. Для же­ла­ю­щих по­нять опи­шем спо­соб сло­же­ния по­дроб­но.

Возь­мём квад­рат­ный лист бу­ма­ги и разо­бьём его на клет­ки, на­при­мер, 4×4. Рас­кра­сим  клет­ки в шах­мат­ном по­ряд­ке в две крас­ки и в каж­дом квад­ра­те из цен­тра пу­стим опре­де­лён­ное ко­ли­че­ство лу­чей. Рас­ста­вим в крас­ных квад­ра­тах зе­лё­ные звёз­доч­ки так, чтобы их раз­мер уве­ли­чи­вал­ся при хож­де­нии по спи­ра­ли. Те­перь сло­жим лист бу­ма­ги в по­лос­ку, за­тем в пря­мо­уголь­ник, и в са­мом кон­це — в тре­уголь­ник. Эта слой­ка устро­е­на сле­ду­ю­щим об­ра­зом. Есть несколь­ко си­них сло­ев в од­ной по­ло­вине, а в дру­гой по­ло­вине — крас­ные слои. Спо­соб по­стро­е­ния зе­лё­ных звёз­до­чек был та­ков, что по­сле про­ве­дён­но­го сло­же­ния они умень­ша­ют­ся к се­ре­дине мно­го­слой­но­го тре­уголь­ни­ка, как бы вло­же­ны друг в дру­га. Нач­нём сми­нать слой­ку так, чтобы си­ние слои шли вы­пук­лым об­ра­зом на­ру­жу и крас­но-зе­лё­ные слои то­же. Мы по­лу­ча­ем по­верх­ность, ко­то­рая, в кон­це кон­цов, скла­ды­ва­ет­ся в плос­кий мно­го­уголь­ник.

У по­лу­чив­ше­го­ся мно­го­уголь­ни­ка есть крас­ное ос­но­ва­ние (си­ние тре­уголь­ни­ки на­хо­дят­ся там же, внут­ри слой­ки) и зе­лё­ная гре­бён­ка. При этом у гре­бён­ки иго­лок столь­ко же, сколь­ко бы­ло зе­лё­ных звёз­до­чек, т. е. крас­ных квад­ра­тов.

А уве­ли­чил­ся ли пе­ри­метр от­но­си­тель­но из­на­чаль­но­го квад­ра­та? Ре­ше­на ли по­став­лен­ная за­да­ча? Ес­ли срав­нить фигу­ры, то вид­но, что пе­ри­метр силь­но умень­шил­ся. За­чем же то­гда скла­ды­ва­ли та­ким слож­ным спо­со­бом?

На кон­крет­ном при­ме­ре был рас­смот­рен об­щий ал­го­ритм. И в этом ал­го­рит­ме есть два па­ра­мет­ра — ко­ли­че­ство кле­ток в раз­би­е­нии из­на­чаль­но­го квад­ра­та и ко­ли­че­ство лу­чей в каж­дом квад­ра­те. По­смот­рим, что бу­дет, ес­ли ме­нять эти па­ра­мет­ры.

При том же раз­би­е­нии 4×4 бу­дем уве­ли­чи­вать ко­ли­че­ство лу­чей внут­ри каж­дой клет­ки. Это при­ве­дёт к утонь­ше­нию иго­ло­чек гре­бён­ки, их мень­ше­му пе­ре­се­че­нию и, со­от­вет­ствен­но, неболь­шо­му уве­ли­че­нию пе­ри­мет­ра.

Есть ещё вто­рой па­ра­метр — ко­ли­че­ство кле­ток раз­би­е­ния из­на­чаль­но­го квад­ра­та. Ес­ли уве­ли­чи­вать этот па­ра­метр, то по по­стро­е­нию бу­дет уве­ли­чи­вать­ся и ко­ли­че­ство иго­лок в гре­бён­ке.

Сов­мест­ное уве­ли­че­ние обо­их па­ра­мет­ров — и ко­ли­че­ства кле­ток, и ко­ли­че­ства лу­чей в каж­дой клет­ке — да­ёт уве­ли­че­ние пе­ри­мет­ра. На­сколь­ко же он мо­жет уве­ли­чи­вать­ся? Ока­зы­ва­ет­ся, до бес­ко­неч­но­сти. А это зна­чит, что в ка­кой-то мо­мент он станет боль­ше, чем пе­ри­метр из­на­чаль­но­го квад­ра­та!

За­да­ча о мя­том руб­ле — по­скла­ды­вать пря­мо­уголь­ник и уве­ли­чить пе­ри­метр — ре­ше­на. Но сколь­ко же раз на­до скла­ды­вать? До­воль­но мно­го. Из ра­бо­ты А. Та­ра­со­ва мож­но по­лу­чить оцен­ку: при раз­би­е­нии 16×16 и ко­ли­че­стве лу­чей в каж­дой клет­ке 16²·30 пе­ри­метр по­лу­чив­ше­го­ся мно­го­уголь­ни­ка бу­дет боль­ше, чем пе­ри­метр из­на­чаль­но­го квад­ра­та.

В филь­ме это по­ка­зать нель­зя, а мож­но ли сде­лать в жиз­ни? Вы на­вер­ня­ка хо­ро­шо помни­те, что сло­жить лист бу­ма­ги, да­же очень тон­кой, мож­но не бо­лее 7—8 раз.  Ес­ли дав­но это не де­ла­ли — про­верь­те про­стым экс­пе­ри­мен­том.  Так что же да­ёт са­ма за­да­ча, по­став­лен­ная В. И. Ар­ноль­дом, и та­кой «нере­а­ли­зу­е­мый» ал­го­ритм? От­та­чи­ва­ние ин­стру­мен­та на­у­ки, ко­то­рый на­вер­ня­ка при­го­дит­ся в даль­ней­шем её раз­ви­тии.

Ли­те­ра­ту­ра

В. И. Ар­нольд. За­да­ча 1956-1 // За­да­чи Ар­ноль­да. Фа­зис, 2000. С. 2.

А. Та­ра­сов. Ре­ше­ние за­да­чи Ар­ноль­да о «мя­том руб­ле» // Че­бы­шев­ский сбор­ник. 2004. Вып. 1. Т. 5. С. 174—187.

А. Пет­ру­нин. Плос­кое ори­га­ми и длин­ный рубль. arXiv:1004.0545v1.

www.etudes.ru

Задача о мятом рубле • Антон Айзенберг • Научно-популярные задачи на «Элементах» • Математика

Эта задача имеет давнюю и интересную историю. Впервые ее, как считается, предложил Владимир Арнольд в 1956 году (и ее можно найти под номером 1 в книге «Задачи Арнольда», М: Фазис, 2000). Название задачи — «Задача о мятом рубле» — обусловлено тем, что рубль в то время был бумажным.

На западе задача также известна как «задача о салфетке Маргулиса» или просто как «задача о складывании салфетки» (Napkin folding problem). По-видимому, первое «решение» задачи предложил американский оригамист Роберт Лэнг (см. Robert J. Lang, а также личный сайт Лэнга), собрав в 1987 году фигурку морского ежа, которая, по сути, дает решение. Немного упрощенную идею решения он описал в 2003 году в книге «Origami design secrets» (к сожалению, пока не переведенной на русский язык). В этой книге он развивает идею разработки моделей оригами при помощи метода оптимальной упаковки кругов. Построение морского ежа можно описать при помощи диаграммы кругов подобно тому, как мы это сделали для тонкого журавлика (рис. 4).

Удивительно, но оказывается, периметр сложенной фигуры можно сделать не просто больше чем периметр исходного листа. Можно сделать его сколь угодно большим. Идея такого построения в том, чтобы повторить конструкцию «тонкого журавлика», описанную выше, много раз вдоль всего листа бумаги, по горизонтали и вертикали. Как раз так и получается морской еж Лэнга. Это позволяет получить сколь угодно много тонких отростков. Нужно только убедиться, что суммарная длина отростков может быть сделана сколь угодно большой.

В построениях Лэнга, однако, было несколько неясных с математической точки зрения моментов. Дело в том, что бумага, как ее понимают оригамисты, отличается от идеальной математической бумаги несколькими параметрами. Самое главное отличие в том, что оригамисты при сборке моделей иногда немного растягивают или сжимают бумагу, а для математической бумаги это запрещено. Математик не поверит в существование фигуры большего периметра, даже если будет держать ее в руках: а вдруг при ее сборке была допущена недопустимая операция? Впрочем, другое отличие бумаги настоящей от математической скорее играет на руку математикам: идеальная бумага не имеет толщины, а, значит, можно накладывать сколько угодно слоев бумаги друг на друга, и гнуть полученный «сэндвич», не боясь, что он порвется или растреплется. Только делать это приходится исключительно в уме. Если вы попробуете сделать очень тонкие отростки, как на рис. 4, — не удивляйтесь, если они получатся потрепанными и некрасивыми.

В 1998 году вышла статья И. Ященко «Make your dollar bigger now!!!» (doi:10.1007/BF03025296), в которой приводится четкое и понятное построение, позволяющее сделать периметр больше, чем у исходного прямоугольника, однако всё же не сколь угодно большим.

Математически строгое доказательство того, что периметр можно сделать сколь угодно большим (а заодно и строгая формулировка задачи), было предложено Алексеем Тарасовым в статье Решение задачи Арнольда о «мятом рубле». Он не знал ни про журавлика, ни про морского ежа, а придумал оригинальную конструкцию, которая получила впоследствии имя «расческа Тарасова».

Идею доказательства, использующую журавлика, я взял из понятной и чрезвычайно наглядной статьи А. Петрунина. Там же вы можете найти детали приведенных здесь рассуждений, подробный исторический обзор, а также решение другой интересной задачи «бумажной геометрии»: можно ли сложить лист бумаги таким образом, чтобы периметр увеличился и результат был выпуклым многоугольником?

Советую также зайти на сайт Математических Этюдов, где наша задача подробно разобрана. Там есть много картинок, в том числе иллюстрирующих построение расчески Тарасова.

Остались тут и нерешенные задачи. Например, до сих пор неизвестно (насколько я знаю), можно ли увеличить периметр, делая лишь «полупростые» складки, как показано на рис. 6: сгибая не вдоль всей прямой, а только вдоль одного отрезка.

elementy.ru

3. Фигура с минимальным периметром

В этом разделе пояснительной записки на примере выбора формы огорода приводится решение задачи определения плоской фигуры заданной площади, имеющей наименьший периметр

3.1. Постановка задачи

Четыре огорода в форме круга, квадрата и двух прямоугольников с отношением сторон 2:1 и 3:1 имеют одинаковую заданную площадь 2000 м². Определить огород, вокруг которого забор будет самым коротким.

3.2. Требования к решению

Для решения задачи необходимо использовать Excel97 с соблюдением следующих требований:

• полное решение разместить на одном рабочем листе;

• заданную площадь огородов представить в верхней части рабочего листа;

• таблицу результатов решения разместить под исходными данными;

• задачу снабдить заголовком, который следует подходящим образом отформатировать;

• в качестве итога расчетов предусмотреть ячейку с длиной самого короткого забора и ячейку с автоматическим указанием формы соответствующего огорода;

• для удобства работы переименовать рабочий лист в соответствии с размещенной на нем информацией;

• после окончания форматирования отменить показ сетки на рабочем листе;

• обеспечить автоматическое изменение результата решения при изменении исходных данных.

Последнее требование является наиболее важным. Оно касается не только числовых исходных данных, но и текстовых (например, форм огородов).

3.3. Анализ задачи

Обозначим заданную площадь огородов буквой S. Составим формулы для вычисления длины заборов вокруг огородов, которая совпадает с периметром соответствующей фигуры.

Рассмотрим сначала огород в форме круга. Поскольку для круга с диаметром Dпериметр равен длинеLокружности, можем написать следующие расчетные формулы

Для квадрата со стороной a периметрPможно вычислить с помощью следующих формул

Переходим к формулам для двух огородов в форме прямоугольников. Обозначим через bменьшую сторону прямоугольника, а черезqотношение его сторон (для первого прямоугольникаq=2, для второго –q=3). Тогда формулы для вычисления периметра в случае прямоугольника можно записать так

Рассмотрим теперь формулы для выбора самого короткого забора вокруг четырех огородов. Пусть i– порядковый номер огорода,P_i– периметрi- го огорода,P_min– искомый минимальный периметр. Тогда можно написать формулу

Обозначим буквой T– форму огорода с самым коротким забором и напишем формулу для ее автоматического вычисления

Легко проверить, что условия задачи позволяют выполнить расчеты по формулам (3.1)-(3.5) и найти решение поставленной задачи.

3.4. Описание решения задачи

Фрагмент рабочего листа Excelс решением задачи об огородах (см. рис. 3.1) дает пример возможного оформления результатов вычислений.

Ввод и форматирование заголовка произведено так, как описано в задачах о платежной ведомости и об оптимальном бизнесе. Заданная площадь огородов введена в ячейку B3. Расчеты, связанные с определением длины заборов вокруг огородов, представлены в табличной форме в ячейках интервалаA4:D8. Первая колонка таблицы представляет варианты формы огородов. Длина заборов (периметры), вычисленная по формулам (3.1)-(3.3), видна во втором столбце таблицы. Вспомогательные величины вычислены в ячейках интервалаD5:D8 и вместе с кратким пояснением в ячейкахC5:C8 образуют третий столбец таблицы (см. рис. 3.1). Например, для квадрата в ячейкуD6 введена формула =КОРЕНЬ(B3), обеспечивающая вычисление стороны, а в ячейкуB6 формула =4*D6 для вычисления периметра. Копирование этих формул в другие ячейки не производилось, поэтому в них можно использовать ссылки на ячейки любого типа. Основу указанных двух формул составляют формулы (3.2) из подраздела 3.3.

Наибольший интерес представляют формулы в ячейках B10 иC10. В ячейкуB10 введена формула =МИН($B$5:$B$8), реализующая вычисление минимального периметраP_minпо формуле (3.4). Более сложна формула в ячейкеC10

=ЕСЛИ(B5=B10;A5;ЕСЛИ(B6=B10;A6;ЕСЛИ(B7=B10;A7;A8)))

Она реализует выбор варианта формы огорода с минимальным периметром в точном соответствии с формулой (3.5). Пояснения по использованию логической функции ЕСЛИ имеются в подразделе 2.4.

studfiles.net

помогите ответить на вопросы пожалуйста))) прошу. Буду благодарна.

1)окружность 2)Нет, не могут. так как многоугольник — выпуклая фигура 3)Элементы треугольника— вершины, стороны, углы. 4)Обозначают буквами латинского алфавита вершины многоугольника называют с любой вершины, но по порядку не пропуская вершины либо по часовой стрелке, либо против часовой стрелки 5)Периметр многоугольника — это сумма длин всех сторон многоугольника 6)Многогранник, у которого две грани, называемые основаниями, равные многоугольники с соответственно параллельными сторонами, а остальные грани, называемые боковыми, являются прямоугольниками, квадратами или параллелограммами 7)Две фигуры называются равными, если все их стороны имеют одинаковую длину

5)Периметр многоугольника — это сумма длин всех сторон многоугольника 6)Многогранник, у которого две грани, называемые основаниями, равные многоугольники с соответственно параллельными сторонами, а остальные грани, называемые боковыми, являются прямоугольниками, квадратами или параллелограммами 7)Две фигуры называются равными, если все их стороны имеют одинаковую длину

touch.otvet.mail.ru