Эллипс и овал разница – Овал и эллипс
Овал в объеме называется. Разница между овалом и эллипсом
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О 1 О 2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О 3 и О 4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.
Построение овала с соприкасающимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0 1 радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О 2 и О 3 .
Рисунок 3.44
Если из точек О 2 и О 3 провести прямые через центры О и O 1 , то в пересечении с опорными окружностями получим точки сопряжения С , C 1 , D и D 1 . Из точек О 2 и О 3 как из центров радиусом R 2 проводят дуги сопряжения.
Построение овала с пересекающимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С 2 и О 3 проводят прямые, например, через центры О
и O 1 до пересечения с опорными окружностями в точках сопряжения С, С 1 D и D 1 , а радиусами R 2 , равными диаметру опорной окружности,- дуги сопряжения.Рисунок 3.45 Рисунок 3.46
Построение овала по двум заданным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пересечения с отрезком АС в точке Е 1 . К середине отрезка АЕ 1 восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O 1 и 0 2 . Строят точки O 3 и 0 4 , симметричные точкам O 1 и 0 2 относительно осей CD и АВ. Точки O 1 и 0 3 будут центрами опорных окружностей радиуса R 1 , равного отрезку О 1 А, а точки O 2 и
В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:
1. имеют точку соприкосновения;
2. пересекаются;
3. не пересекаются.
Рассмотрим первый случай. Строят отрезок OO 1 =2R, параллельный оси Х, на его концах (точки О и О 1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R 1 =2R. Из точек пересечения вспомогательных окружностей О 2 и О 3 строят дуги CD и C 1 D 1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C 1 D 1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.
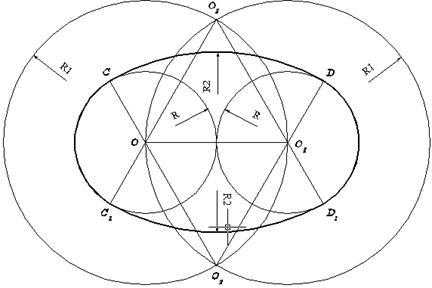
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Что такое овал и эллипс
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – посто
windows10official.ru
Как называется объемный овал. Разница между овалом и эллипсом
геометрический овал с одной осью симметрии
3. Овал в инженерной графике
В инженерной графике под овалом обычно понимают фигуру с двумя осями симметрии, построенную на сочетании четырех участков кривых двух радиусов. Отрезки дуг выбраны так, что обеспечивается плавный переход от одного радиуса кривизны к другому. Точка, движется по периметру овала всегда находится на одном из двух фиксированных радиусов кривизны (в отличие от эллипса , где радиус кривизны постоянно меняется).
4. Овал в геометрии
Так же, как в обыденной речи, в геометрии математический термин «овал» встречается в названиях различных геометрических фигур более или менее овальной формы, но без точного определения овала как такового. Общее между этими кривыми, что это обычно кривые замкнутые, выпуклые, гладкие (с касательной в любой точке) и имеют по крайней мере одну ось симметрии.
Термин «овалоид» употребляют в яйцевидных поверхностей образованных вращением овальной кривой вокруг одной из ее осей симметрии.
Другие примеров овалов можно отнести.
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Что такое овал и эллипс
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс
Разница между овалом и эллипсом
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:
Объём. Овал – более широкое понятие, в объём которого входит эллипс.
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Определение
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если раз
Определение овала. Разница между овалом и эллипсом
Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.
Что такое овал и эллипс
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
Разница между овалом и эллипсом
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
TheDifference.ru определил, что отличие овала от эллипса заключается в следующем:
Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О 1 О 2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О 3 и О 4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.
Построение овала с соприкасающимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0 1 радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О 2 и О 3 .
Рисунок 3.44
Если из точек О 2 и О 3 провести прямые через центры О и O 1 , то в пересечении с опорными окружностями получим точки сопряжения С , C 1 , D и D 1 . Из точек О 2 и О 3 как из центров радиусом R 2 проводят дуги сопряжения.
Построение овала с пересекающимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С 2 и О 3 проводят прямые, например, через центры О и O 1 до пересечения с опорными окружностями в точках сопряжения С, С 1 D и D 1 , а радиусами R 2 , равными диаметру опорной окружности,- дуги сопряжения.
Рисунок 3.45 Рисунок 3.46
Построение овала по двум заданным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пересечения с отрезком АС в точке Е 1 . К середине отрезка АЕ 1 восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O 1 и 0 2 . Строят точки O 3 и 0 4 , симметричные точкам O 1 и 0 2 относительно осей CD и АВ. Точки O 1 и 0 3 будут центрами опорных окружностей радиуса R 1 , равного отрезку О 1 А, а точки O 2 и 0 4 — центрами дуг сопряжения радиуса R 2 , равного отрезку О 2 С. Прямые, соединяющие центры O 1 и 0 3 с O 2 и 0 4 в пересечении с овалом определят точки сопряжения.
В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:
1. имеют точку соприкосновения;
2. пересекаются;
3. не пересекаются.
Рассмотрим первый случай. Строят отрезок OO 1 =2R, параллельный оси Х, на его концах (точки О и О 1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R 1 =2R. Из точек пересечения вспомогательных окружностей О 2 и О 3 строят дуги CD и C 1 D 1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C 1 D 1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.
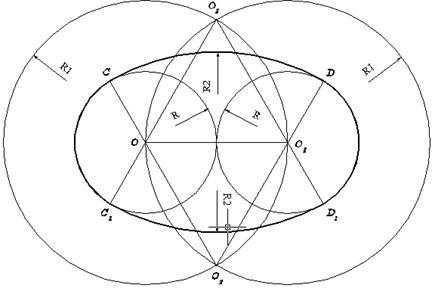
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса
геометр
fashionlife33.ru
Разница между овалом и эллипсом.
Фигура, представляющая собой объемный овал имеет следующее название — эллипсоид. Эллипсоиды могут иметь как вытянутую, так и приплюснутую форму.
Эллипсоид можно представить вот таким вот образом как на изображениях ниже:
А вот немного об этой фигуре:
Фигура, которая своей формой похожа на объмные овал, носит название quot;эллипсоидquot;. Источником для происхождения этого названия послужили два греческих слова:
Во Вселенной эта форма очень распространена: е имеют все планеты Солнечной системы, форма известных галактик также является эллиптической.
Если фигура напоминает объемный овал, скорее всего это перевернутые эллипс или эллипсоид.
А вот то, чем они различны.
Это эллипс, фигура изображенная на плоскости.
Это эллипсоид. Эллипс в пространстве и в объеме.
Скорее всего вы имеете в виду вот такую фигуру, как на фото ниже
своееобразное яйцо, ведь яйцо — это и есть овал. Такая фигура носит название вытянутый эллипсоид .
Эллипсоиды бывают и приплюснутые, они выглядит уже вот так:
Центр эллипосида лежит в начале координат. Эллипсоид имеет свою каноническую формулу:
В трхмерном пространстве объмная фигура, которая со стороны напоминает овал носит название — эллипсоид.
Если окунуться в мир формул, то основные параметры эллипсоида можно определить согласно следующим вычислениям:
Фигура, которая представляет собой объемный овал, называется эллипсоид . По форме эллипсоиды бывают вытянутые и приплюснутые. Самый наглядный пример приплюснутого эллипсоида — планета Земля, да и все остальные планеты Солнечной системы.
Если круг в объме, это шар, то овал в объме, это не что иное как эллипсоид. Примечательно, что данное слово пишется с двумя буквами quot;лquot;, поэтому не ошибитесь при написании.
Данная фигура мннее распространена, нежели куб или пирамила, и даже параллелепипед. Обычно в школе на уроках геометрии мы не так часто имеем дело с такими фигурами как эллипсоид. Оно и понятно, ведь правила и методы вычисления искомых значений в таких фигурах достаточно сложны.
Примером эллипсоида может служить спелый арбуз но не шарообразной формы, а именно немного вытянутой, то есть овальный в сечении. Есть и другие предметы в нашем обиходе. Часто в форме эллипсоидов делают каменные изделия из редких минералов для коллекционеров.
Вспоминая геометрию с ее фигурами, где окромя плоских фигур есть еще и объемные, надо бы добавить, что эллипс (как плоская фигура) есть одна из разновидностей овала. Поэтому, как вариант, одним из ответов может считаться эллипсоид , а вот еще один объемный овал — овоид , в простонародье называемый яйцом.
Объемный овал имеет название эллипсоид.
Эллипсоид вращения имеет название сфероид. Эллипсоид вращения может быть сплюснутым и вытянутым.
Вот как выглядит сплюснутый эллипсоид вращения:
вот так выглядит вытянутый эллипсоид вращения:
Фигура, представляющая собой объемный овал — это элипсоид. Еще элипсоид можно определить как сферу, сечение которой выглядит, как овал. Частным случаем эллипсоида является сфероид это тело, которое получается в результате вращением овала (эллипса) вокруг своей оси.
Фигура, напоминающая объемный овал называется эллипсоид. Такая фигура довольно часто встречается в жизни. Например, такую форму имеет любимый многми арбуз, наша земля, а так же, все планеты солнечной системы.
Если память не изменяет это либо Эллипсоид либо Геоид. Последний конечно относится к форме Земли, приближнно принимаемой за объмный овал.
В инженерной графике под овалом обычно понимают фигуру с двумя осями симметрии, построенную на сочетании четырех участков кривых двух радиусов. Отрезки дуг выбраны так, что обеспечивается плавный переход от одного радиуса кривизны к другому. Точка, движется по периметру овала всегда находится на одном из двух фиксированных радиусов кривизны (в отличие от эллипса , где радиус кривизны постоянно меняется).
Так же, как в обыденной речи, в геометрии математический термин «овал» встречается в названиях различных геометрических фигур более или менее овальной формы, но без точного определения овала как такового. Общее между этими кривыми, что это обычно кривые замкнутые, выпуклые, гладкие (с касательной в любой точке) и имеют по крайней мере одну ось симметрии.
Термин «овалоид» употребляют в яйцевидных поверхностей образованных вращением овальной кривой вокруг одной из ее осей симметрии.
Другие примеров овалов можно отнести.
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О 1 О 2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О 3 и О 4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теор
brendoptom.ru
Разница между овалом и эллипсом
геометрический овал с одной осью симметрии
3. Овал в инженерной графике
В инженерной графике под овалом обычно понимают фигуру с двумя осями симметрии, построенную на сочетании четырех участков кривых двух радиусов. Отрезки дуг выбраны так, что обеспечивается плавный переход от одного радиуса кривизны к другому. Точка, движется по периметру овала всегда находится на одном из двух фиксированных радиусов кривизны (в отличие от эллипса , где радиус кривизны постоянно меняется).
4. Овал в геометрии
Так же, как в обыденной речи, в геометрии математический термин «овал» встречается в названиях различных геометрических фигур более или менее овальной формы, но без точного определения овала как такового. Общее между этими кривыми, что это обычно кривые замкнутые, выпуклые, гладкие (с касательной в любой точке) и имеют по крайней мере одну ось симметрии.
Термин «овалоид» употребляют в яйцевидных поверхностей образованных вращением овальной кривой вокруг одной из ее осей симметрии.
Другие примеров овалов можно отнести.
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О 1 О 2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О 3 и О 4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.
Построение овала с соприкасающимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0 1 радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О 2 и О 3 .
Рисунок 3.44
Если из точек О 2 и О 3 провести прямые через центры О и O 1 , то в пересечении с опорными окружностями получим точки сопряжения С , C 1 , D и D 1 . Из точек О 2 и О 3 как из центров радиусом R 2 проводят дуги сопряжения.
Построение овала с пересекающимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С 2 и О 3 проводят прямые, например, через центры О и O 1 до пересечения с опорными окружностями в точках сопряжения С, С 1 D и D 1 , а радиусами R 2 , равными диаметру опорной окружности,- дуги сопряжения.
Рисунок 3.45 Рисунок 3.46
Построение овала по двум заданным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пересечения с отрезком АС в точке Е 1 . К середине отрезка АЕ 1 восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O 1 и 0 2 . Строят точки O 3 и 0 4 , симметричные точкам O 1 и 0 2 относительно осей CD и АВ. Точки O 1 и 0 3 будут центрами опорных окружностей радиуса R 1 , равного отрезку О 1 А, а точки O 2 и 0 4 — центрами дуг сопряжения радиуса R 2 , равного отрезку О 2 С. Прямые, соединяющие центры O 1 и 0 3 с O 2 и 0 4 в пересечении с овалом определят точки сопряжения.
В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:
1. имеют точку соприкосновения;
2. пересекаются;
3. не пересекаются.
Рассмотрим первый случай. Строят отрезок OO 1 =2R, параллельный оси Х, на его концах (точки О и О 1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R 1 =2R. Из точек пересечения вспомогательных окружностей О 2 и О 3 строят дуги CD и C 1 D 1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C 1 D 1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

Рисунок Построение
stacys.ru
Чем отличается овал от эллипса?
Эллипс — это строгое геометрическое понятие (ГМТ, сумма растояний от которых до двух заданных фиксирована) . А овал — просто округлая фигура.
Согласно определению овал-это выпуклая замкнутая кривая на плоскости с непрерывно изменяющейся касательной (т. е. гладкая кривая — квадрат же по этому определению не может быть овалом — он НЕ ГЛАДКИЙ и касательная на его углах испытывает скачки: производная имеет разрывы первого рода). . Эллипс же относится к кривым второго порядка и получается сечением конуса-вместе с параболой и гиперболой он составляет т. н. конические сечения. . Если рассматривать эллипс исходя из определения овала, то эллипс будет замкнутой плоской кривой и касательная к любой его точке будет непрерывно меняться (условие гладкости соблюдено). . Значит эллипс будет относится к категории овалов, как частный случай..
Овал состоит из дуг окружностей, а эллипс — нет.
Дядя Митя единственный, кто совершенно правильно ответил. В черчении эллипсы заменяют овалами, строить которые не в пример легче, чем энти эллипсы…
Все эллипсы — овалы, но не все овалы — эллипсы. (x²+y²)²-2c²(x²-y²)=a⁴-c⁴ — овал Кассини.
touch.otvet.mail.ru